为什么我只会一堆大众题啊!!
还没更完的:假装更完了.jpg
Day1 T1
显然取链上代价前最小的若干个付银币,于是主席树上二分即可。
Day1 T2
首先想一个 dp 做法出来。
考虑做一个线头 dp 类似的东西。从左到右扫,状态中记录现在还没有结束的线头个数。
仔细思考一下,要记录 Fake 策略 下还未结束的线头个数和 Optimal 策略 下还未结束的线头个数,状态数为 \(n^3\)。
发现有一维度不用计入状态,只需要乘上系数,状态数变成 \(n^2\)。
Day1 T3
想了很久这题不会,又想了很久发现是原题...
首先有一些基础的思考,比如一个点 \(u\) 能一步跳到 \(v\) 的话就可以松弛 \(ans_v+1 \to ans_u\)。现在的问题就是对于每个点 \(u\) 算出跳到 \(1\) 和 \(n\) 的最小步数(跳到 \(1,n\) 就相当于跳到所有点)。
然后发现要求的就是 这题,于是线段树优化建图就做完了。
Day2 T1
看错题意以为会一直移动,然后卡了很久。。。。。。。
询问次数是 \(\log\) 的,这启发我们想一些一次询问出某个比例的边的做法。
对于第一次:把所有点按照 \(dep\bmod 3\) 分成 3 类,对于某一类的点全部放上球然后询问。容易发现这样不同层的球移动不会互相影响,就可以问出 \(cnt\) 条边。取最多个数的一类,则 \(cnt\ge n/3\)。
接下来的每一轮,取三个类中 还有出边没问出来的点 最多 的一类,放上球然后询问。每次都至少问出三分之一的出边。
询问次数是 \(\lceil\log_3 n\rceil\le 29\)。
Day2 T2
对于去掉每个人 \(i\),有一些类是再去掉一票就寄了的,有一些类是再去掉一票也贡献不变的。
设每个 \(i\) 删掉它会对哪些集合票数减 0 的集合为 \(msk_i\)。那就是询问一个集合 \(T\),求出 \(\max_{j\ne i}(\text{popcount}(T\&msk_j))\)。
先子集和再超集和就可以处理。
Day2 T3
首先有一个每次都暴力 DP 的做法,但这样太暴力了,很难用数据结构维护,也很难区间询问。
于是尝试发现一些可以维护的性质/贪心结论。
发现小的一段长度一定为 \(1\),大的一段长度一定 \(\le 2\log V\),不然一定不优。
如果直接在线段树上维护(记录两端的大段长度),可以获得 \(Q\log n\log^2 V\) 的做法,和暴力一个分
然后想一想可以贪心的性质/结论。下面“取一个数”指将一个数作为小段。设 \(T=2\log V\),就是大段的最长可能长度。
设 \(f(i)\) 表示 \(j<i\),\(j\) 和 \(i\) 能同时取,且 \(j\) 最大的那个位置。
设 \(nxt(i)\) 表示最小的 \(j(j>i)\) 使得 \(f(j)\ge i\)。如果 \(nxt(i)>i+V\) 则设 \(nxt(i)=i+V\),对答案没有影响。
容易发现如果当前小段选的是 \(i\),下一个小段一定可以贪心选 \(nxt(i)\)。(如果选了 \(nxt(i)\) 不满足可以调整 \(i\))
枚举开头的一个点 \(i(i\in [l,l+T])\),不断跳 \(i\to nxt(i)\to nxt(nxt(i))...\) 表示我们选小段的最后一个位置。
从 \(i\) 跳到 \(r\) 附近的一个点 \(x(x\in [r-T,r])\),然后判一堆边界情况,计算一下答案。
边界情况太恶心了,对拍出一堆边界情况。。解释不清楚,建议直接看代码
修改的时候,容易发现只有 \(O(\log V)\) 个点的 \(nxt\) 会被修改。并且 \(nxt\) 构成一棵树,可以直接用 LCT 维护树。
复杂度 \(Q\log V(\log V+\log N)\)。
Day3 T1
首先画出一条折线,A 向右上方走一格,B 向右下方走一格。
交换两个 A,B 可以看作把折线的某个位置从“下上”翻成了“上下”。
把一条折线变成另一条折线的代价就是两条折线之间的面积。
经过一些贪心、手玩可以发现,就是把一条初始的折线经过若干次向上翻后,可以包含住 \(m\) 个“峰”。下图是一种 \(m=3\) 的情况,黄色部分为翻上去的代价。
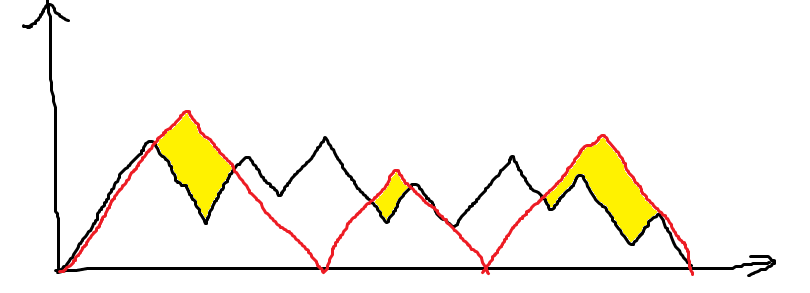
然后就可以写出 dp,设 \(f_{i,j}\) 为第 \(j\) 个峰的结束位置是 \(i\) 的代价。
转移是 \(f_{i,k}+cost(i,j)\to f(j,k+1)\)。\(cost\) 就是上图黄色的面积,可以预处理以后 \(O(1)\) 计算。
然后突然发现 dp 的第二维是有凸性的!于是可以 wqs 二分。
发现转移是有决策单调性的,直接类似 [IOI2000] 邮局 做,就可以 \(O(n\log n\log V)\)。评测机很慢,过不太去,只有 87 分。
但上面那个做法实在是脑子傻了,发现转移分讨一下就可以斜率优化了,一次 dp 为 \(O(n)\),时间复杂度 \(O(n\log V)\)。
Day3 T2
经过一些猜猜猜交交交,发现 在可行的情况下,选大的 box 越多就是越好的。
可以写出一个 DP,设 \(dp_{t,i,j}\) 表示考虑了前 \(t\) 大的 box,选了 \(i\) 个 box,放了 \(j\) 个 cookies 是否可行。
复杂度是 \(n^3\) 的,经过一些循环卡上下界可以跑 \(n=3000\) 获得 85pts
我错了,这个复杂度是 \(n^2\log n\) 而不是 \(n^3\):由于是从大到小加 box,所以“选了 \(i\) 个 box”这一维只需要转移到 \(n/b_i\) 的。这一维总转移最多就是 \(n/n+n/(n-1)+..+n/1 = n\ln n\)。
然后加上 bitset 优化,就可以做到 \(\frac{n^2\log n}{w}+n^2\),可以通过。
Day3 T3
我的做法太垃圾了。
要求出一个区间内点的虚树包含的边集大小。
根据[ZJOI2019]语言,两颗 dfs 序不相交的虚树是可以合并边集大小的信息的。
设 \(s,t\) 为 dfs 序最大、最小的点,那么
s=l.s
t=r.t
val=l.val+r.val-Dep(Lca(l.t,r.s))
看做平面上有 \(m\) 个点 \((i,dfn_{a_i})\)。
发现就是询问一个矩形内的信息并,并且是有顺序(按 dfs 序合并)的信息并。可以直接用 CF1375H trick 处理(分块+分治),时间复杂度 \(O(n\sqrt n)\)。
不过显然有更简单的做法。
扫描线右端点,然后每次加一个点就是在 LCT 上 Access 一下,把每个颜色段都修改一下。
复杂度 \(O(n\log^2 n)\)。
Day4 T1
通信题。主要是要还原 \(x,y\) 的信息。
可以选一些位置钦定来表示 \(x,y\) 的信息。在每种情况下,钦定的部分 一些位置会被 ban,一些位置可以填,在可以填的位置编一个属于这种 \(x,y\) 的 pattern。需要编的 pattern 在任何情况下都不冲突,这样 Bob 可以解码出 \(x,y\)。
但这样还是占用了比较多的格子。可以在 钦定的部分 里有一些表示 \(x,y\),有一些表示 \(S\),还是要求任意两个方案不冲突。
选对角线相关的格子应该能卡到 \(n=42\)。
zky 说他选的是左上角 3*4 的格子,可以卡到 \(n=43\)。
Day4 T2
对于树的做法:
答案是所有边权的 \(w_x+w_y\),加上最大的 \(w_i\),减去所有的 \(w_i\)。
\(Q=0\) 就是最小生成树。
现在解决 \(Q>0\) 的情况,就是在原树上砍 \(k\) 条边,加 \(k\) 条边,使得代价最小。
由于一定会把每个连通块的最小连到全局最小,这就相当于 让割开后的每个连通块 \(\sum \min w_i\) + 没割掉的边权 最小。
考虑给割开后的每个连通块“定一个根”,并且让根为连通块权值最小的点时答案最小。定一个根后,把每条边的贡献看作父亲的点权。答案就是所有边父亲的点权加上所有点的点权(这样恰好是每条边的边权+根的点权)。容易发现这样的答案下,根选权值最小的点答案最小。
把每条边看作两条有向边。于是就转化成了 \(k-\) 最小有向生成森林的问题,可以直接用最小树形图的算法解决!
具体可以看 2020 集训队论文 张哲宇,最小内向森林问题。网上的blog
复杂度 1log。
Day4 T3
折返的次数是 \(\log V\),直接暴力找折返就是 \(n\log n\log V\)。
也可以用值域分段 trick 变成 \(n\log V\)。