第九题(Chinese Remainder Theorem)
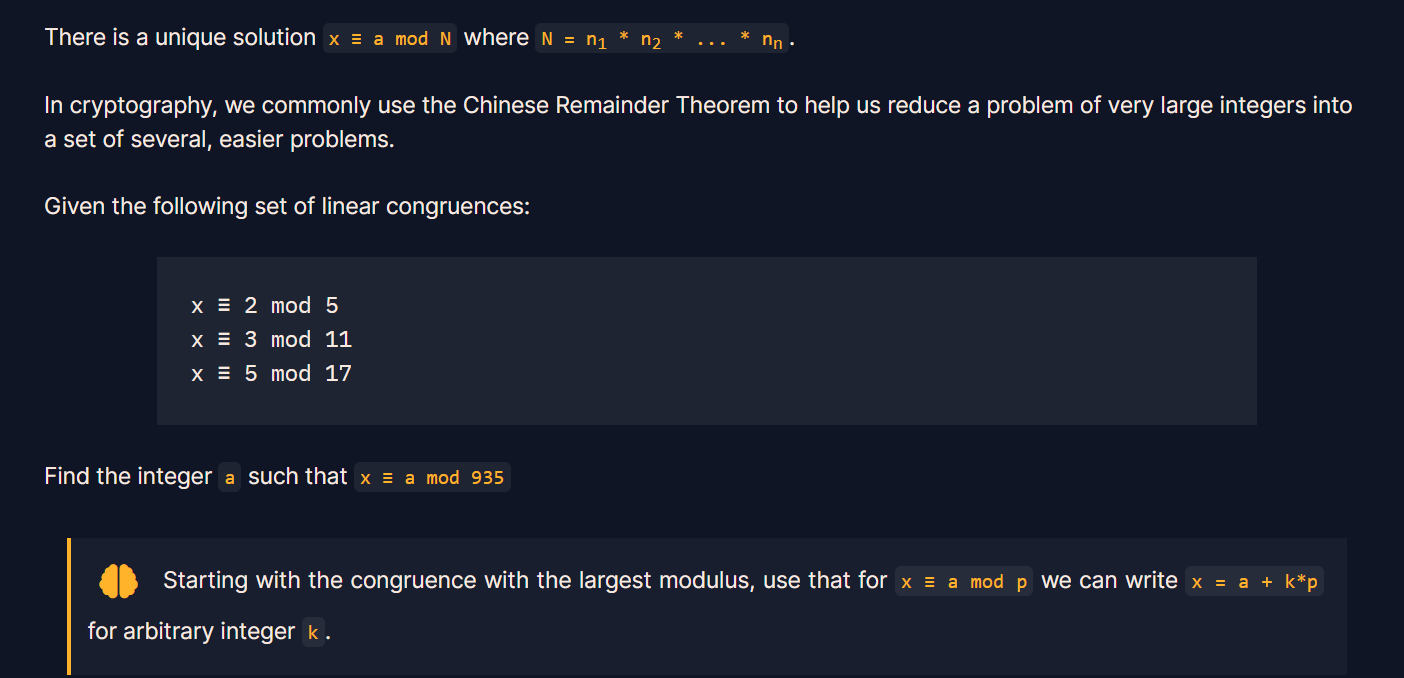
考察中国剩余定理
这个讲的挺详细的[https://www.bilibili.com/video/BV1gf4y1S7LR/]
参考:[(https://www.cnblogs.com/MashiroSky/p/5918158.html)]
我这里就不做过多的赘述了。
然后给出代码:
from functools import reduce
from math import gcd
# 定义同余方程组和模数
eqns = [(2, 5), (3, 11), (5, 17)]
moduli = [5, 11, 17]
# 计算总模数
N = reduce(lambda x, y: x*y, moduli)
# 计算每个模数的逆元
m = [N // m for m in moduli]
mi = [pow(m[i], -1, moduli[i]) for i in range(len(moduli))]
# 计算唯一解
x = sum(a * mi[i] * m[i] for i, (a, _) in enumerate(eqns))
# 输出结果
print("Solution: x = {} (mod {})".format(x % N, N))
第十题(Adrien's Signs)
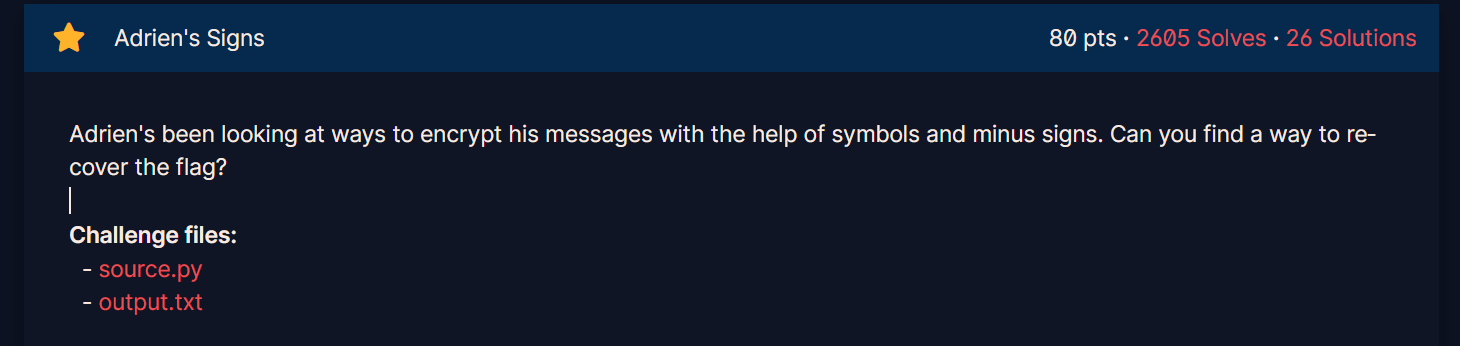
加密代码如图:

上面的代码实现了一个基本的加密方案,用于加密一个二进制格式的标志(flag)。其中,标志的每一位都被独立地加密。加密过程使用了一个基于模幂运算的公钥算法。
公钥由两个参数组成:一个大素数 p 和一个整数 a,其中 a 是模 p 的一个原根。私钥是指数 e,每一位明文都随机选择一个私钥指数。
为了加密单个二进制位,首先将明文位转换为整数 0 或 1。然后,在 1 到 p-1 之间随机选择一个指数 e。对于该位的密文,计算如下:
如果明文为 1,则密文为 a^e mod p
如果明文为 0,则密文为 -a^e mod p
每个位的密文存储在一个列表中,并作为函数的输出返回。
代码中的 FLAG 变量实际上没有被使用,只是一个占位符,用于加密的标志应该作为参数传递给 encrypt_flag 函数。
给出解密代码:
a = 288260533169915
p = 1007621497415251
exec('c=' + open("D:\\temp\\5.txt").read())
from sympy import discrete_log as dl
from tqdm import * #应用tqdm库显示过程进度
ff = ''
for i in trange(len(c)):
cc = c[i]
try:
r = dl(p,cc,a)
ff += '1'
except:
r = dl(p,-cc%p,a)
ff += '0'
print(ff)
import libnum
print(libnum.b2s(ff))
第十一题(Modular Binomials)
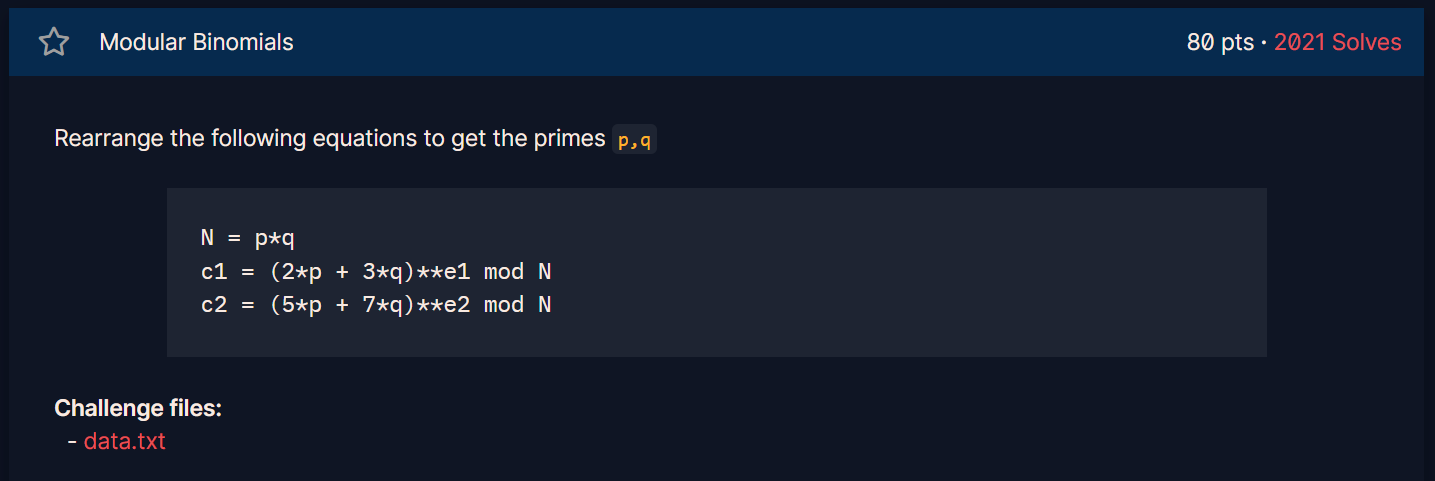
题目说要拿到p,q,第一想法时看一下能不能分解,用factordb试着分解了一下,发现竟然可以

成功拿到p,q。
这道题是一道典型的模二项式的题,可以用模算数定理进行简化,这边我找到了一位师傅的推算:
https://img-blog.csdnimg.cn/20210122100125578.jpg
具体实现代码如下:
from math import gcd
n = 14905562257842714057932724129575002825405393502650869767115942606408600343380327866258982402447992564988466588305174271674657844352454543958847568190372446723549627752274442789184236490768272313187410077124234699854724907039770193680822495470532218905083459730998003622926152590597710213127952141056029516116785229504645179830037937222022291571738973603920664929150436463632305664687903244972880062028301085749434688159905768052041207513149370212313943117665914802379158613359049957688563885391972151218676545972118494969247440489763431359679770422939441710783575668679693678435669541781490217731619224470152467768073
e1 = 12886657667389660800780796462970504910193928992888518978200029826975978624718627799215564700096007849924866627154987365059524315097631111242449314835868137
e2 = 12110586673991788415780355139635579057920926864887110308343229256046868242179445444897790171351302575188607117081580121488253540215781625598048021161675697
c1 = 14010729418703228234352465883041270611113735889838753433295478495763409056136734155612156934673988344882629541204985909650433819205298939877837314145082403528055884752079219150739849992921393509593620449489882380176216648401057401569934043087087362272303101549800941212057354903559653373299153430753882035233354304783275982332995766778499425529570008008029401325668301144188970480975565215953953985078281395545902102245755862663621187438677596628109967066418993851632543137353041712721919291521767262678140115188735994447949166616101182806820741928292882642234238450207472914232596747755261325098225968268926580993051
c2 = 14386997138637978860748278986945098648507142864584111124202580365103793165811666987664851210230009375267398957979494066880296418013345006977654742303441030008490816239306394492168516278328851513359596253775965916326353050138738183351643338294802012193721879700283088378587949921991198231956871429805847767716137817313612304833733918657887480468724409753522369325138502059408241232155633806496752350562284794715321835226991147547651155287812485862794935695241612676255374480132722940682140395725089329445356434489384831036205387293760789976615210310436732813848937666608611803196199865435145094486231635966885932646519
q1 = pow(c1, e2, n)
q2 = pow(c2, e1, n)
d = pow(5, e1 * e2, n) * q1 - pow(2, e1 * e2, n) * q2
q = gcd(d, n)
p = n // q
assert(p * q == n)
print(p,q)