正常的 trie 树能解决一些字符串问题,\(0/1\) trie 能解决最大异或和问题。但是如果每次询问是针对一个区间的,那么普通 trie 就不好做了,此时就需要可持久化 trie 树。
类似可持久化线段树,对于每个版本新建一个 \(root\) (相当于每个前缀建),在插入时该继承的继承,改修该的修改。和普通 trie 一样,\(tr_{p,u}\) 表示 \(p\) 号节点连向字符为 \(u\) 的点的编号。那么每次插入的流程如下:
- 新建当前字符串的根节点 \(p\),并记 \(pre\) 表示上一个字符串的根节点。
- 若当前字符为 \(u\),那么给 \(u\) 新开一个节点 \(tr_{p,u}=++cnt\)。
- 同时还要继承 \(pre\) 的其他字符,也就是对于一个字符 \(ch \ne u\),\(tr_{p,ch}=tr_{pre,ch}\),相当于直接连过去。
- 接着让 \(p=tr_{p,u},pre=tr_{pre,u}\),向下建树,重复 \(1,2,3\),直到建完。
举个例子:若当前要插入这些字符串:\(\texttt{cat,cup,soup,cut}\)。(黑色点为根节点)
第一次:
第二次: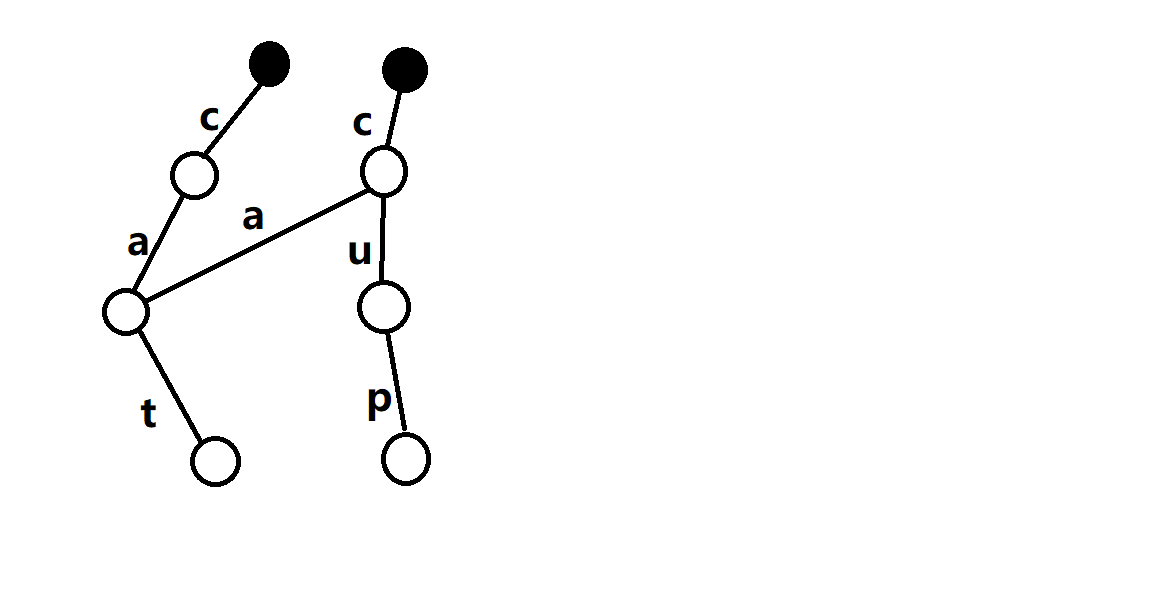
第三次: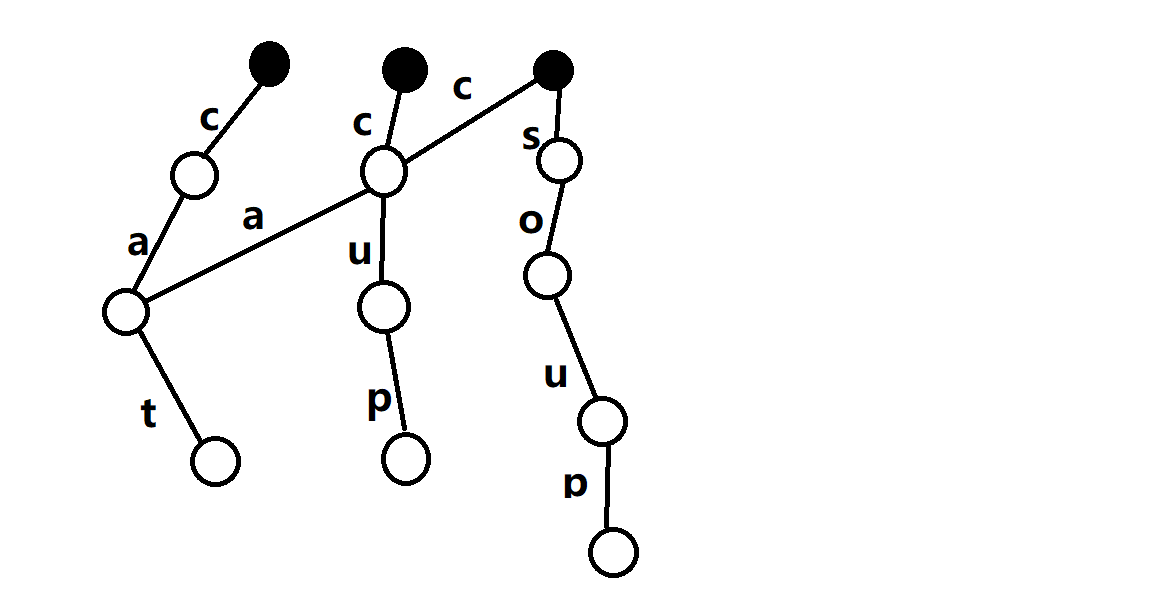
第四次: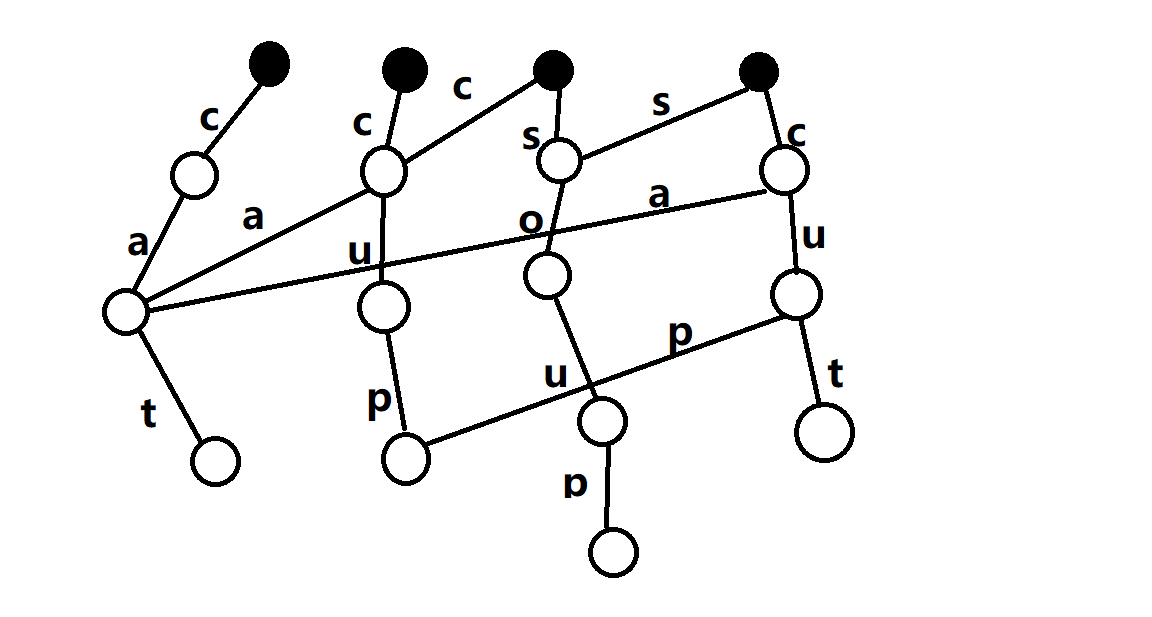
这样,一棵 trie 就建好了,从第 \(i\) 个 \(root\) 出发,我们能访问到 \(1 \sim i\) 的所有字符串,这就把问题解决一半了。只需沿用可持久化线段树的思想,前缀相减即可。
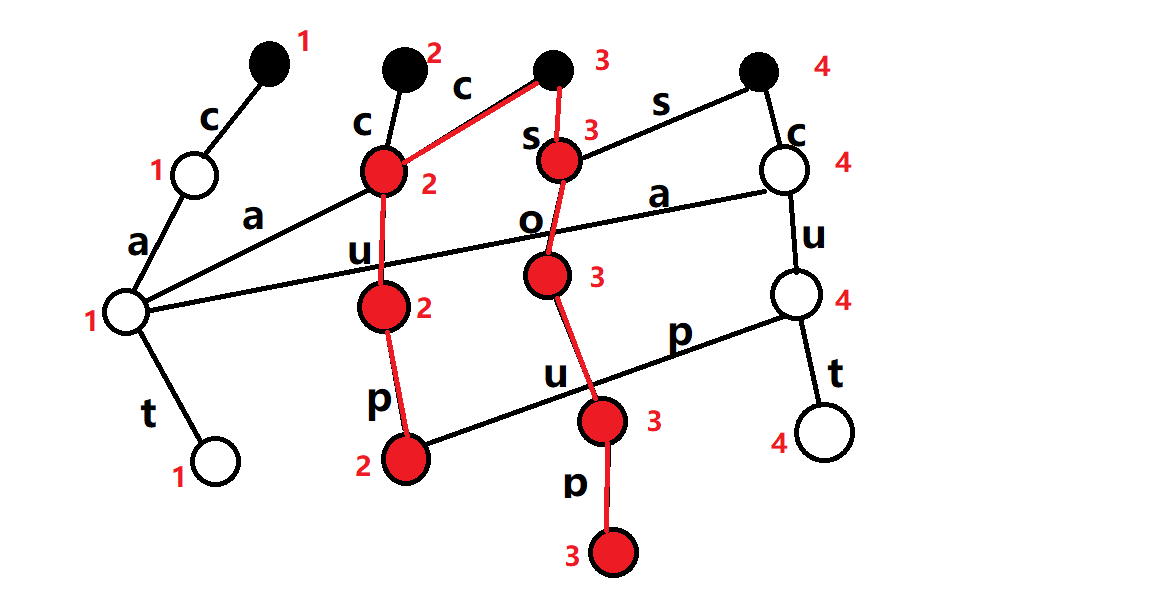
具体来说,我们需要引入一个 \(last\) 数组来表示每个点是第几次被插入的,如果在遍历过程中发现有个点的 \(last < l\) 了,那么他就不在我们的询问范围内,就可以直接返回了。如下图,红色数字就是每个节点的 \(last\) 值:

例如我们要访问区间 \([2,3]\),则应从 \(root_3\) 进入,访问 \(last\ge 2\) 的点,下图红色点和边可以被访问:
code
以 \(0/1\) trie 为例。
插入:
void insert(int pre,int p,int i,int k){//pre上一个数字的root,p当前数字的root,i是第几次插入的,k是这个数字要拆分的二进制位数
if(k<0){
last[p]=i;//建完了,返回
return;
}
int u=(num[i]>>k)&1;
if(pre)tr[p][u^1]=tr[pre][u^1];//继承上一个的字符
tr[p][u]=++cnt;
insert(tr[pre][u],tr[p][u],i,k-1);//递归新建节点
last[p]=max(last[tr[p][0]],last[tr[p][1]]);//更新last,从子树更新上来,也可以直接赋为i
}
查询(这里返回的是最大值的下标):
int query(int p,int x,int l,int k){//p当前节点,对于区间[l,r]赋为root[r],x是要查询的数,l左边界,来判断当前数是否在[l,r]中,k是二进制下第几位
if(k<0)return last[p];//last 相当于这个数的下标,因为我们是按前缀顺序插入的
int u=(x>>k)&1;
if(last[tr[p][u^1]]>=l)return query(tr[p][u^1],x,l,k-1);//在区间[l,r]中就优先走有贡献的位置
return query(tr[p][u],x,l,k-1);//否则不产生贡献,向下走
}
例题
板子。先记 \(s\) 为 \(a\) 的前缀异或和,那么询问的式子就可以转化为求一个 \(p \in [l-1,r-1]\),使得 \(x \oplus s_n \oplus s_p\) 最大。\(x\oplus s_n\) 是已知的,那么就只需要用可持久化 trie 在 \([l-1,r-1]\) 中查找一个 \(s_p\) 让他们异或起来值最大就行了。
注意:最好一开始 insert 一个 \(0\),因为很多题都是前缀和查询,会涉及到 \(l-1=0\) 的情况,不管他就 gg 了。
还是用 \(s\) 表示前缀异或和,那么我们就要求前 \(k\) 大的 \(s_r \oplus s_{l-1}\)。先不考虑前 \(k\) 大的限制,思考最大怎么做。一个想法是固定右端点,求出对于这个右端点最大的是什么。这样再在每个右端点中取 \(\max\) 就得到答案了。
再回头看题,前 \(k\) 大,每一对都是两个数 \(s_i,s_j\) 异或在一起,不难想到这道题。我们可以沿用此题的思路,把每个 \(r\) 对应的最大的点的信息放入一个堆中。具体信息有:当前的右端点、和右端点异或起来的最大值所在位置、这个最大值所在位置的区间范围(一个左端点一个右端点)、当前最大值是什么。有了这些,我们就每次拿出最大的那个元素,并把答案累加。然后设当前最大值位于 \(pos\),右端点位于 \(rx\),\(pos\)所在区间为 \([l,r]\),因为不能有重复区间,因此在 \([l,pos-1]\) 中找一个和 \(rx\) 最大的位置,再在 \([pos+1,r]\) 中找一个,把他们放入堆中,重复 \(k\) 次就行了。