本文思路来自伟大的@FxorG
二分的单调性:如果\(mid\)可以,那么小于\(mid\)的也一定可以(从每排末尾剔除一些人即可)。
主要问题是贪心的选法。
原问题所引出的可能得选人的方案可能是离散的,比如:
2
2 5
当每排人数是2时,一下方案是一种最优解:
1个身高为1的,1个身高为2的
1个身高为1的,1个身高为2的
2个身高为2的
如果把人看成一条柱:
总共3组,我们发现,他们的下标(身高)范围是\([1,2],[1,2],[2,2]\)。
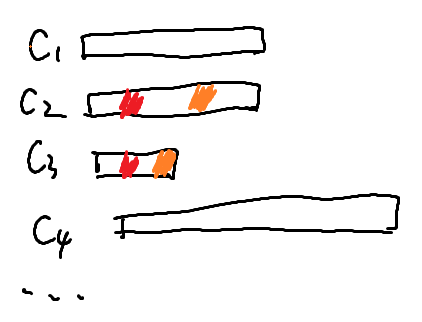
也就是说,我们选取的方案之间可能会有交集(就像上面的红色和橙色,虽然相同身高的人与人之间没有区别,但是不管你怎么交换,它们还是“交叉的”)。
先考虑没有交集的情况怎么贪心,也就是说不同身高的人只会被搭配一次。
那么方案大概长这样:
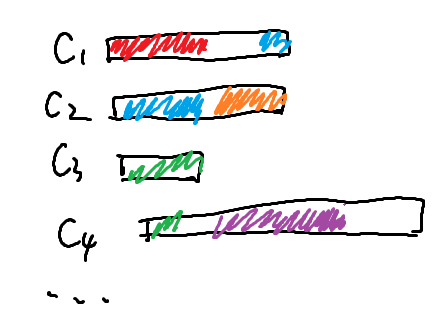
把人看成线段上的点,那么选法就是一条条线段,每个人只能被分进一排,等价于点只能被覆盖一次,也就是P1803 凌乱的yyy / 线段覆盖。
为了方便理解,先把人标上编号,看成有区别的。
这个时候有点问题,就是人可能不是连续的:
但是因为人实际上没有区别,你可以把它们移动到贴在一起,变成连续的。上述“交叉”的方案就是阻碍了我们将方案变成连续的一段段线段。
现在考虑如何去调整有“交叉”的选法,让它变成连续的线段。
其实就是说身高差了1的两种人最多只会配对一次。
假设在\(i,i+1\)处有交叉,也就是\(i,i+1\)配对了两次。
假设第一排中\(i,i+1\)人数分别是\(a,b\),第二排中人数分别是\(c,d\),则有\(a+b=len,c+d=len\)。
我们想要让它们分成自己内部的一条线段和一条跨身高的线段。
\(a+b+c+d=2len\),则必然有\(a+c\ge len\)或\(b+d\ge len\)。(反证,假设都\(<len\),矛盾)。
于是必然可以把它们中的一部分分到自己内部和跨身高的部分。
然后就是线段覆盖问题了,因为区间长度一样,左端点排序等价于右端点排序。