[NOI2016] 区间

题目描述

在数轴上有 $n$ 个闭区间从 $1$ 至 $n$ 编号，第 $i$ 个闭区间为 $[l_i,r_i]$。

现在要从中选出 $m$ 个区间，使得这 $m$ 个区间共同包含至少一个位置。换句话说，就是使得存在一个 $x$ ，使得对于每一个被选中的区间 $[l_i,r_i]$，都有 $l_i \leq x \leq r_i$。

对于一个合法的选取方案，它的花费为被选中的最长区间长度减去被选中的最短区间长度。

区间 $[l_i,r_i]$ 的长度定义为 $(r_i-l_i)$，即等于它的右端点的值减去左端点的值。

求所有合法方案中最小的花费。如果不存在合法的方案，输出 $-1$。

输入格式

第一行包含两个整数，分别代表 $n$ 和 $m$。

第 $2$ 到第 $(n + 1)$ 行，每行两个整数表示一个区间，第 $(i + 1)$ 行的整数 $l_i, r_i$ 分别代表第 $i$ 个区间的左右端点。

输出格式

输出一行一个整数表示答案。

样例 #1

样例输入 #1

6 3
3 5
1 2
3 4
2 2
1 5
1 4

样例输出 #1

2

提示

样例输入输出 1 解释

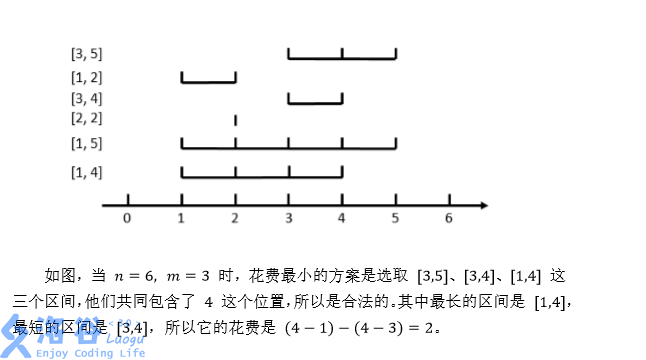
数据规模与约定

本题共 20 个测试点，各测试点信息如下表。

对于全部的测试点，保证 $1 \leq m \leq n$，$1 \leq n \leq 5 \times 10^5$，$1 \leq m \leq 2 \times 10^5$，$0 \leq l_i \leq r_i \leq 10^9$。

解题思路

  一开始想歪了，后面看题解发现可以二分就试了下，不过会超时。首先答案具有二段性，如果差值的最小值是 $\text{ans}$，那么当二分出差值为 $\text{mid}$，$\text{mid} \geq \text{ans}$，则至少存在一组合法方案，即某个点被 $m$ 个区间覆盖且 $m$ 个区间的差值不超过 $\text{mid}$（$\text{ans}$ 对应的方案就是一组合法方案）。当 $\text{mid} < \text{ans}$ 则不存在任何合法方案。

  当二分出 $\text{mid}$ 后如何检查是否存在合法方案呢？对区间按照长度从小到大排序，然后依次枚举每个区间，维护一个指针 $j$，当枚举到第 $i$ 个区间时，如果 $len_{i} - len_{j} > \text{mid}$，则往右移动 $j$，直到差值不超过 $\text{mid}$，那么从 $j$ 到第 $i$ 就是要选择的区间。另外还需要用线段树来动态维护每个点被覆盖的次数，以及被覆盖最多次数是多少。如果在这个过程中发现某个位置被覆盖次数超过 $m$，则找到一个合法方案。

  TLE 代码如下，时间复杂度为 $O(\log{10^9} \cdot n \log{n})$：

#include <bits/stdc++.h>
using namespace std;

const int N = 5e5 + 10, M = N * 2;

int n, m;
int l[N], r[N], p[N];
int xs[M], sz;
struct Node {
    int l, r, mx, add;
}tr[M * 4];

void build(int u, int l, int r) {
    if (l == r) {
        tr[u] = {l, r, 0, 0};
    }
    else {
        int mid = l + r >> 1;
        build(u << 1, l, mid);
        build(u << 1 | 1, mid + 1, r);
        tr[u] = {l, r, 0, 0};
    }
}

void pushdown(int u) {
    if (tr[u].add) {
        tr[u << 1].mx += tr[u].add;
        tr[u << 1].add += tr[u].add;
        tr[u << 1 | 1].mx += tr[u].add;
        tr[u << 1 | 1].add += tr[u].add;
        tr[u].add = 0;
    }
}

void modify(int u, int l, int r, int c) {
    if (tr[u].l >= l && tr[u].r <= r) {
        tr[u].mx += c;
        tr[u].add += c;
    }
    else {
        pushdown(u);
        int mid = tr[u].l + tr[u].r >> 1;
        if (l <= mid) modify(u << 1, l, r, c);
        if (r >= mid + 1) modify(u << 1 | 1, l, r, c);
        tr[u].mx = max(tr[u << 1].mx, tr[u << 1 | 1].mx);
    }
}

int find(int x) {
    int l = 1, r = sz;
    while (l < r) {
        int mid = l + r >> 1;
        if (xs[mid] >= x) r = mid;
        else l = mid + 1;
    }
    return l;
}

bool check(int mid) {
    build(1, 1, sz);
    for (int i = 1, j = 1; i <= n; i++) {
        modify(1, find(l[p[i]]), find(r[p[i]]), 1);
        while (r[p[j]] - l[p[j]] + mid < r[p[i]] - l[p[i]]) {
            modify(1, find(l[p[j]]), find(r[p[j]]), -1);
            j++;
        }
        if (tr[1].mx >= m) return true;
    }
    return false;
}

int main() {
    scanf("%d %d", &n, &m);
    for (int i = 1; i <= n; i++) {
        scanf("%d %d", l + i, r + i);
        xs[++sz] = l[i];
        xs[++sz] = r[i];
        p[i] = i;
    }
    sort(xs + 1, xs + sz + 1);
    sz = unique(xs + 1, xs + sz + 1) - xs - 1;
    sort(p + 1, p + n + 1, [&](int i, int j) {
        return r[i] - l[i] < r[j] - l[j];
    });
    int l = 0, r = 1e9 + 1;
    while (l < r) {
        int mid = l + r >> 1;
        if (check(mid)) r = mid;
        else l = mid + 1;
    }
    if (l > 1e9) l = -1;
    printf("%d", l);
    
    return 0;
}

  想一下能不能把二分的部分去掉。在检查的过程中本质是想知道是否存在差值不超过 $\text{mid}$ 的区间使得某个点被覆盖至少 $m$ 次。那么可以直接用双指针来维护，当枚举到第 $i$ 个区间，假设选择从 $i$ 到左边某个区间使得某个点被覆盖至少 $m$ 次，且距离 $i$ 最近的是 $j$，那么从 $j$ 到第 $i$ 就是要选择的区间，且以 $i$ 为右端点时差值是最小的。可以发现随着 $i$ 往右移动，$j$ 也之后往右移动，具有单调性，可以用双指针。

  其中如果想到固定所选区间的最大长度，然后找到在满足条件下的尽可能长的长度最小的区间，那么就会想到双指针。

  AC 代码如下，时间复杂度为 $O(n \log{n})$：

#include <bits/stdc++.h>
using namespace std;

const int N = 5e5 + 10, M = N * 2;

int n, m;
int l[N], r[N], p[N];
int xs[M], sz;
struct Node {
    int l, r, mx, add;
}tr[M * 4];

void build(int u, int l, int r) {
    if (l == r) {
        tr[u] = {l, r, 0, 0};
    }
    else {
        int mid = l + r >> 1;
        build(u << 1, l, mid);
        build(u << 1 | 1, mid + 1, r);
        tr[u] = {l, r, 0, 0};
    }
}

void pushdown(int u) {
    if (tr[u].add) {
        tr[u << 1].mx += tr[u].add;
        tr[u << 1].add += tr[u].add;
        tr[u << 1 | 1].mx += tr[u].add;
        tr[u << 1 | 1].add += tr[u].add;
        tr[u].add = 0;
    }
}

void modify(int u, int l, int r, int c) {
    if (tr[u].l >= l && tr[u].r <= r) {
        tr[u].mx += c;
        tr[u].add += c;
    }
    else {
        pushdown(u);
        int mid = tr[u].l + tr[u].r >> 1;
        if (l <= mid) modify(u << 1, l, r, c);
        if (r >= mid + 1) modify(u << 1 | 1, l, r, c);
        tr[u].mx = max(tr[u << 1].mx, tr[u << 1 | 1].mx);
    }
}

int find(int x) {
    int l = 1, r = sz;
    while (l < r) {
        int mid = l + r >> 1;
        if (xs[mid] >= x) r = mid;
        else l = mid + 1;
    }
    return l;
}

int main() {
    scanf("%d %d", &n, &m);
    for (int i = 1; i <= n; i++) {
        scanf("%d %d", l + i, r + i);
        xs[++sz] = l[i];
        xs[++sz] = r[i];
        p[i] = i;
    }
    sort(xs + 1, xs + sz + 1);
    sz = unique(xs + 1, xs + sz + 1) - xs - 1;
    sort(p + 1, p + n + 1, [&](int i, int j) {
        return r[i] - l[i] < r[j] - l[j];
    });
    build(1, 1, sz);
    int ret = 2e9;
    for (int i = 1, j = 1; i <= n; i++) {
        modify(1, find(l[p[i]]), find(r[p[i]]), 1);
        while (tr[1].mx >= m) {
            modify(1, find(l[p[j]]), find(r[p[j]]), -1);
            if (tr[1].mx < m) {
                modify(1, find(l[p[j]]), find(r[p[j]]), 1);
                break;
            }
            j++;
        }
        if (tr[1].mx == m) ret = min(ret, r[p[i]] - l[p[i]] - (r[p[j]] - l[p[j]]));
    }
    if (ret == 2e9) ret = -1;
    printf("%d", ret);
    
    return 0;
}

参考资料

  题解 P1712 【[NOI2016]区间】：https://www.luogu.com.cn/blog/zykykyk/solution-p1712

本栏目推荐文章
• Windows Server 2016 & 2019 工作站速配脚本
• 【LeetCode 2494. 合并在同一个大厅重叠的活动】MySQL用户变量编程解决区间合并问题
• 2016-4-3、路径解析
• P8649 [蓝桥杯 2017 省 B] k 倍区间
• [COCI2015-2016#2] VUDU 题解
• CTSC 2016 香山的树
• 区间合并
• R语言无套利区间模型：正向套利和反向套利次数、收益率分析华泰柏瑞300ETF可视化
• P4093 [HEOI2016/TJOI2016] 序列 题解
• [Noi Online #1 入门组] 跑步 题解

区间 2016 NOI区间2016 noi p1587 2016 noi 2016 noi noi 2023 noi 游记2023 noi noi-linux 2016 p2305 2014 noi 题解2023 noi