概
本文提出了一种新的框架, 在前向的过程中, 可以逐步将相似的 nodes 和他们的特征聚合在一起.
符号说明
- \(\mathcal{G} = \{\mathcal{E, V}\}\), 图;
- \(|\mathcal{V}| = N\);
- \(\mathbf{A} \in \mathbb{R}^{N \times N}\), 邻接矩阵;
- \(\mathbf{X} \in \mathbb{R}^{N \times d}\), node feature matrix
Graph Coarsening
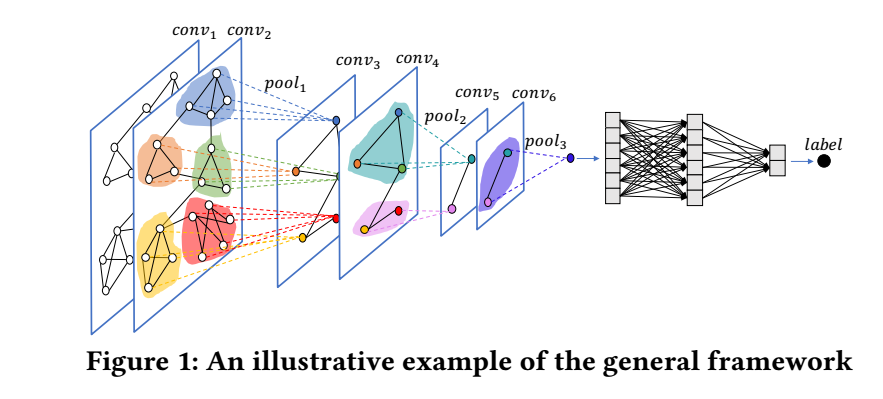
-
下面的过程可以是整个流程中的任一一层.
-
首先通过类似谱聚类的聚类方法将所有的 nodes 分成不重合的 \(K\) connected 的 subgraphs \(\{\mathcal{G}^{(k)}\}_{k=1}^K\). 并令 \(\Gamma^{(k)}\) 表示 \(\mathcal{G}^{(k)}\) 中的结点, 其数量为 \(N_k\).
-
定义采样算子 \(\mathbf{C}^{(k)} \in \{0, 1\}^{N \times N_k}\):
\[\mathbf{C}^{(k)}[i, j] = 1 \quad \text{ if and only if } \Gamma^{(k)}(j) = v_i. \]通俗地来看, \(\mathbf{C}^{(k)}\) 的任一一行刻画了 \(v_i\) 在 \(\Gamma^{(k)}\) 中的位置 (全为 0 则表示不属于该子图), 显然有:
\[(\mathbf{C}^{(k)})^T \mathbf{C}^{(k)} = \mathbf{I}. \] -
于是, 对于任意的(完整图上的)图信号 \(\mathbf{x} \in \mathbb{R}^{N \times 1}\), 我们可以通过
\[\mathbf{x}^{(k)} = (\mathbf{C}^{(k)})^T \mathbf{x}, \]下采样来得到子图 \(\mathcal{G}^{(k)}\) 上的信号.
-
有了子图上的信号, 我们也可以通过上采样
\[\bar{\mathbf{x}} = \mathbf{C}^{(k)} \mathbf{x}^{(k)}, \]‘恢复’出信号 (显然, 只有对应子图的部分非零).
-
类似地, 我们可以得到子图的邻接矩阵:
\[\mathbf{A}^{(k)} = (\mathbf{C}^{(k)})^T \mathbf{A}\mathbf{C}^{(k)}. \] -
而 intra-subgraph 邻接矩阵为
\[\mathbf{A}_{int} = \sum_{k=1}^K \mathbf{C}^{(k)} \mathbf{A}^{(k)} (\mathbf{C}^{(k)})^T, \]可以看到, 实际上就是对每个子邻接矩阵进行上采样然后加和. 显然 \(\mathbf{A}_{int}\) 的非零元素为不包含那些子图子图间的交互.
-
于是
\[\mathbf{A}_{ext} = \mathbf{A} - \mathbf{A}_{int} \]的非零元素即为子图-子图间的交互.
-
为了进一步将其变为 \(K \times K\) 大小以便后续的使用, 定义 \(\mathbf{S} \in \mathbb{R}^{N \times K}\) 为:
\[\mathbf{S}[i, j] = 1 \quad \text{ if and only if } v_i \in \Gamma^{(j)}. \] -
将每个子图看成一个 supernode, 则它们的零阶矩阵为:
\[\mathbf{A}_{coar} = \mathbf{S}^T \mathbf{A}_{ext} \mathbf{S}. \]实际上:
\[[\mathbf{A}_{coar}]_{ij} = \sum_{u \in \Gamma^{(i)}} \sum_{v \in \Gamma^{(j)}} [\mathbf{A}_{ext}]_{uv}. \]
EigenPooling
-
现在, 我们只需要得到 supernode 的节点表示就完成了整体的传播过程, 一种可行的方案是:
\[\text{Pool}((\mathbf{C}^{(k)})^T \mathbf{X}), \]其中 \(\text{Pool}\) 可以是 sum, mean, max 等等. 但是作者认为, 这种 pooling 方式没有抓住图的结构信息, 所以提出了 EigenPooling.
-
假设 \(\mathbf{L}^{(k)}\) 为子图 \(\mathcal{G}^{(k)}\) 的拉普拉斯矩阵,
\[\mathbf{u}_1, \ldots, \mathbf{u}_{N_k}^{(k)} \]为拉普拉斯矩阵的特征向量组.
-
进一步地, 我们将其上采样得到:
\[\bar{\mathbf{u}}_l^{(k)} = \mathbf{C}^{(k)} \mathbf{u}_l^{(k)}, l=1\ldots N_k. \] -
综合所有的子图的信息, 我们可以得到
\[\Theta_l = [\bar{\mathbf{u}}_l^{(l)}, \ldots, \bar{\mathbf{u}}_l^{(K)}] \in \mathbb{R}^{N \times K}, \quad l=1,2, \ldots, H. \]这里 \(H\) 是认为给定的一个值, 需要注意的是, 对于那些 \(N_k < H\) 的子图, 我们取其超出部分的特征向量为 \(\bm{0}\).
-
对于每个 \(\Theta_l\) 我们可以得到 pooling 的结果:
\[\mathbf{X}_l = \Theta_l^T \mathbf{X}, \]总共有
\[\mathbf{X}_{coar} = \mathbf{X}_{pooled} = [\mathbf{X}_1, \ldots, \mathbf{X}_H]. \] -
对于这部分的理论分析这里就不讲了.
代码
- Convolutional EigenPooling Networks Graph withconvolutional eigenpooling networks graph classification convolutional imagenet networks convolutional segmentation biomedical networks convolutional stochastic reduction networks convolutional segmentation networks semantic recommendation convolutional networks hamming convolutional distilling knowledge networks skeleton-based convolutional recognition networks convolutional networks neural cnn fully-convolutional convolutional networks tracking