蒙德里安的梦想 - 状态压缩动态规划
题意
求把 \(N \times M\) 的棋盘分割成若干个 \(1 \times 2\) 的长方形,有多少种方案。
样例输入
2 4
样例输出
5
算法
状态压缩动态规划 (状压DP)
\(\to\) OI-WIKI
状态压缩,顾名思义,就是将某一种状态压缩成容易储存的形式。
最常见的压缩方式即压缩成二进制,将多种 0 和 1 的状态以二进制的方式存储起来。
解题思路
0. 思路
对于本题,我们要先有一个总体思路。
如果要把 \(1 \times 2\) 的长方形横着或竖着放,那么不难发现,如果若干个横着摆放的长方形在某一刻摆到了合理的位置上,那么就有且只有一种方案,使得可以再摆若干个竖着的长方形并摆满剩余空位。
例如,如果此时摆放横着的长方形的状态如下:
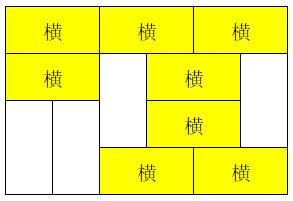
那么竖着的长方形就只有下图一种方案全部摆满:
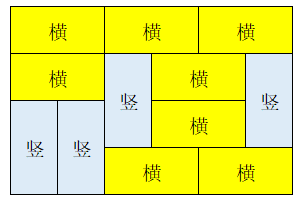
因此,我们只需要求出有多少种合理的横着摆放长方形的方案即可。
1. 确定状态
我们以 \(f_{i, j}\) 表示第 \(i\) 列压缩后的状态为 \(j\) 时的方案数。
这里的 \(j\) 实际是一个二进制数,我们把它转化成十进制,表示的是对于 \(i-1\) 列的横着摆放的长方形对于第 \(i\) 列所造成的影响。
再例如下图:

那么,对于这种状态下,\(f_2\) 的 \(j\) 值就应该是 \((11000)_2\),也就是 \((24)_{10}\)。
其中二进制表示下,
第 \(1\) 位 \(1\) 表示在第 \(1\) 列的横置长方形中的第 \(1\) 行里多出 \(1\) 块到了第 \(2\) 列;
第 \(2\) 位 \(1\) 表示在第 \(1\) 列的横置长方形中的第 \(2\) 行里多出 \(1\) 块到了第 \(2\) 列;
第 \(3\) 位 \(0\) 表示在第 \(1\) 列的横置长方形中的第 \(3\) 行里没有多出 \(1\) 块到了第 \(2\) 列;
第 \(4\) 位 \(0\) 表示在第 \(1\) 列的横置长方形中的第 \(4\) 行里没有多出 \(1\) 块到了第 \(2\) 列;
第 \(5\) 位 \(0\) 表示在第 \(1\) 列的横置长方形中的第 \(5\) 行里没有多出 \(1\) 块到了第 \(2\) 列。
2. 划分阶段
划分阶段即确定求解顺序。
for(int i=1; i<=m; i++){ // 枚举每 1 列
for(int j=0; j<pow2(n); j++){ // 枚举 f[i][j] 中的前项
for(int k=0; k<1<<n; k++){ // 枚举 f[i][j] 中的后项
do_something();
}
}
}
3. 决策选择
对于确定动态转移方程,首先需要判断会不会产生冲突。
冲突1,在同 1 个格子上放了两个长方形
如图,在同 1 个格子上放了两个长方形:
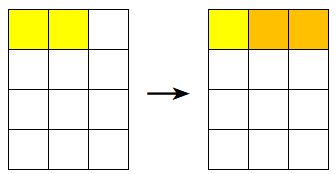
处理这个冲突很简单,只需要判断2个 \(j\) 在二进制表示下有没有在同 1 个位置出现两个 1 即可。
如何判断呢?我们可以利用 & 运算,检查最终两个 \(j\) 与运算后的结果是不是 0。如果时代表没有冲突,否则反之。
bool flag1 = !(j & k);
冲突2,余下的格子中无法放下竖置长方形
如图,余下的格子中无法放下竖置长方形:
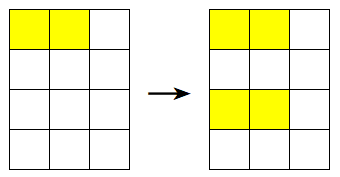
不难发现,如果两行棋子之间的空位为奇数个,则无法放下竖置长方形。
判断两行棋子之间的空位是否为奇数个,也就是将 2 个 \(j\) | 运算后检查其二进制中连续0的个数。
for(int i=1; i<=pow2(n); i++){
st[i] = 1;
int cnt = 0; // cnt 表示 i 在二进制下当前连续 0 的个数
for(int j=1; j<=n; j++){
if(i >> j & 1){ // 如果 i 在二进制表示下的第 j 位是 1
if(cnt % 2){ // 如果存在及数个0
st[i] = false; // 标记为 false
break; // 提前退出
}
}
else{
cnt++; // 否则如果是 0,cnt自增表示0的个数加1
}
}
if(cnt & 1){ // 最后 1 次判断,同上
st[i] = false;
}
}
bool flag2 = st[j | k];
4. 边界条件
在第 1 列,且没有上一列对本列的影响时,设为只有 \(1\) 种方案,即不放。
f[0][0] = 1; // n, m 都从 0 开始
5. 求解目标
最终答案为最后 1 列的下一列的 \(j\) 值为 0,也就是最后 1 列没有横置长方形对下一列有影响时的值。
ans = f[m][0]; // n, m 都从 0 开始
代码
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
#define int long long
const int N = 12, M = 1 << N;
int n, m;
int f[N][M];
bool st[M];
// pow2(x) 表示的是 2^x 的值
int pow2(int x){
return (1 << x);
}
signed main()
{
// 读入
cin >> n >> m;
// 统计 i 在二进制下当前连续 0 的个数是否为奇数
for(int i=0; i<pow2(n); i++){
st[i] = 1;
int cnt = 0; // cnt 表示 i 在二进制下当前连续 0 的个数是
for(int j=0; j<n; j++){
if(i >> j & 1){ // 如果 i 在二进制表示下的第 j 位是 1
if(cnt % 2){ // 如果存在奇数个0
st[i] = false; // 标记为 false
break; // 提前退出
}
}
else{
cnt++; // 否则如果是 0,cnt自增表示0的个数加1
}
}
if(cnt & 1){ // 最后 1 次判断,同上
st[i] = false;
}
}
f[0][0] = 1; // 边界为 1
for(int i=1; i<=m; i++){ // 枚举每 1 列
for(int j=0; j<pow2(n); j++){ // 枚举 f[i][j] 中的前项
for(int k=0; k<1<<n; k++){ // 枚举 f[i][j] 中的后项
// 如果两种冲突都不存在
if(!(j & k) && st[j | k]){
// 方案数增加为上一列的 k 状态
f[i][j] += f[i-1][k];
}
}
}
}
// 输出
cout << f[m][0] << '\n';
return 0;
}