这东西以前觉得挺难的,但是那是因为没好好学。
我不会告诉你我是因为订正模拟赛的需要才好好学了一遍qwq
我觉得这种优化还是借助题目来学习,更加容易理解(而且不难)。
P2619 [国家集训队] Tree I
虽然说是 dp 优化,但是我感觉这道题好像没有 dp。
不妨设它需要 \(ned\) 条边。
首先考虑没有白边限制的情况下,这里有一个高妙的算法就是:并查集。
然后我们令 \(f_x\) 表示白边数量是 \(x\) 的最小生成树,接着我们发现这种东西一定是先下降一段,再上升一段。
所以我们将 \((x,f_x)\) 画在二维平面上,盲猜它形成下凸包的图形(这是题解告诉我的qwq)。
考虑用一个斜率 \(k\) 去切这个图形,则切点所对应的直线的截距一定是最小的,即:
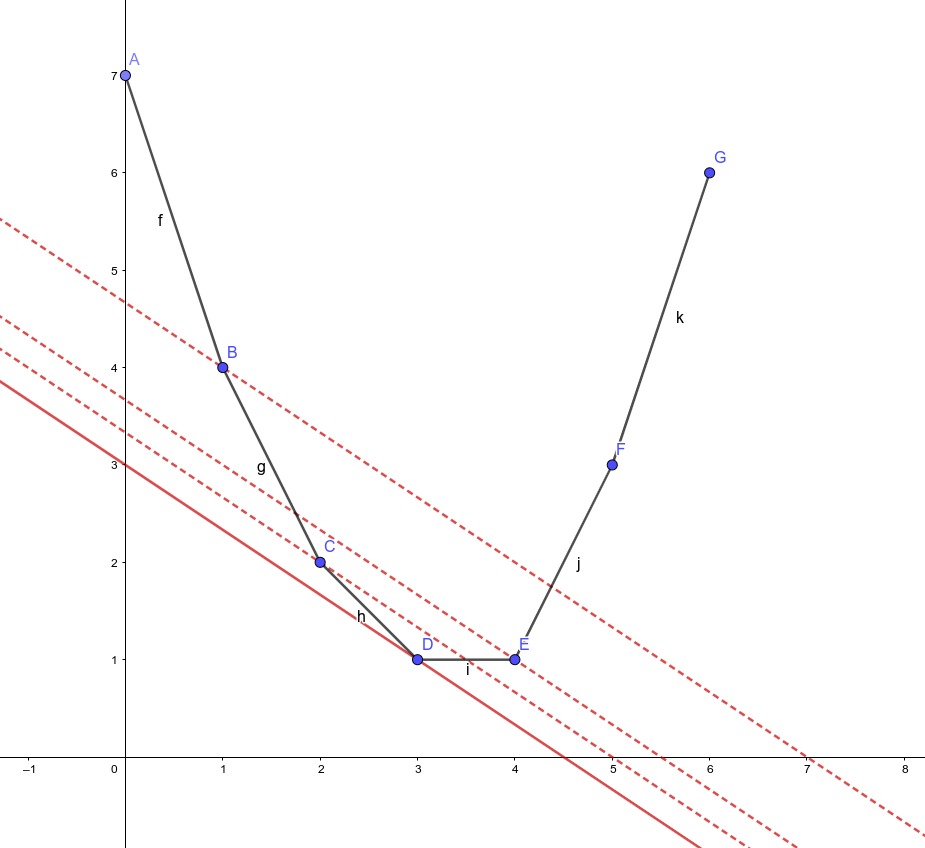
显然对于每个点 \((x,f_x)\),且截距应该是 \(g_x = f_x - k \times x\)。
对于 \(g_x\) 的意义,就是每条白边的边权减少 \(k\),白边数量是 \(x\) 的最小生成树。
而 \(g_x\) 最小,固然就是:每条白边边权减少 \(k\) 后,整个图的最小生成树。
记录一下最小生成树所选的白边数量 \(p\),可以得到斜率为 \(k\) 的直线切这个图形的交点 \((p,f_p)\)。
所以呢,现在就考虑如何找到斜率 \(k\),使得我们可以得到 \(f_{ned}\),wqs二分这个知识点告诉我们,也许可以二分。
跟着斜率 \(k\) 的增大,我们可以发现切点也是不断增大,所以可以直接二分找到这个斜率 \(k\),就能求出 \(f_{ned}\)。
有一种情况就是,图形可能出现三点共线的情况,比如 \(x,ned,y\) 而对于这种情况,我们只需要在贪心的时候选优先选白边即可,因为我们二分是找到最小的可以选择的斜率,而对于 \(y\) 最小可以选择的斜率,由三点共线可得,一定是这三个点所组成的斜率,故而 \(ned\) 也是可以选择这个斜率的。
代码异常好些qwq
#include <bits/stdc++.h>
using namespace std;
int rd() {
int x = 0, f = 1;
char ch = getchar();
while (!('0' <= ch && ch <= '9')) {
if (ch == '-') f = -1; ch = getchar();
}
while ('0' <= ch && ch <= '9') {
x = (x << 1) + (x << 3) + (ch ^ 48); ch = getchar();
}
return x * f;
}
void wr(int x) {
if (x < 0) putchar('-'), x = -x;
if (x >= 10) wr(x / 10); putchar(x % 10 + '0');
}
const int N = 1e5 + 10;
struct union_find {
int n, f[N];
void init(int nn) {
n = nn; for (int i = 1; i <= n; ++i) f[i] = i;
}
int find (int x) {
if (f[x] == x) return x;
return f[x] = find(f[x]);
}
bool merge (int x, int y) {
if (find(x) == find(y)) return false;
f[find(x)] = find(y); return true;
}
} T;
struct node {
int u, v, w, col;
node (int uu = 0, int vv = 0, int ww = 0, int coll = 0) {
u = uu; v = vv; w = ww; col = coll;
}
bool operator < (const node res) const {
if (w != res.w) return w < res.w;
return col < res.col;
}
} p[N];
int n, m, ned;
int u[N], v[N], w[N], col[N];
pair<int,int> check (int x) {
for (int i = 1; i <= m; ++i) {
if (col[i] == 0) p[i] = node(u[i], v[i], w[i] - x, col[i]);
else p[i] = node(u[i], v[i], w[i], col[i]);
}
sort (p + 1, p + m + 1); T.init(n);
int num = 0, sum = 0;
for (int i = 1; i <= m; ++i) {
if (T.merge (p[i].u, p[i].v)) num += (!p[i].col), sum += p[i].w;
}
return make_pair(num,sum);
}
int main() {
n = rd(); m = rd(); ned = rd();
for (int i = 1; i <= m; ++i) u[i] = rd(), v[i] = rd(), w[i] = rd(), col[i] = rd();
for (int i = 1; i <= m; ++i) ++u[i], ++v[i];
int l = -100, r = 100;
while (l < r) {
int mid = (l + r) >> 1;
if (check(mid).first >= ned) r = mid; else l = mid + 1;
}
printf ("%d\n", check(l).second + ned * l);
return 0;
}
总结
总之,wqs二分就是:没有限制的时候好做,加上限制后是凸的。
至于凸的怎么证,打打表猜一猜也许可行?(反正我不会其他方法qwq)。