定义
wqs 二分一般解决恰好选 \(m\) 个的问题,且关于 \(m\) 的函数 \(f(m)\) 为凸函数(\(f(m)\) 表示恰好选 \(m\) 个的最优解)。
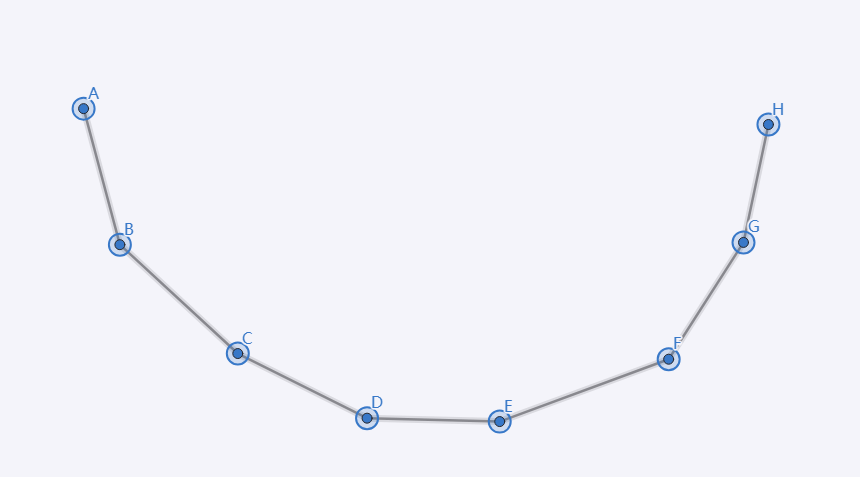
上图为 \(f(m)\) 函数。
二分斜率 \(k\),假设每选一次都要减去 \(k\),则 \(f'(x)=f(x)-kx\),设使得 \(f'(x)\) 的最小值为 \(t\),则 \(t\) 关于 \(k\) 单调不减。
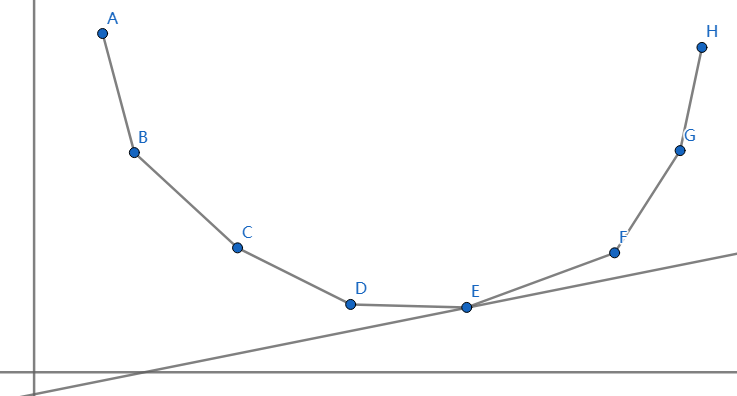
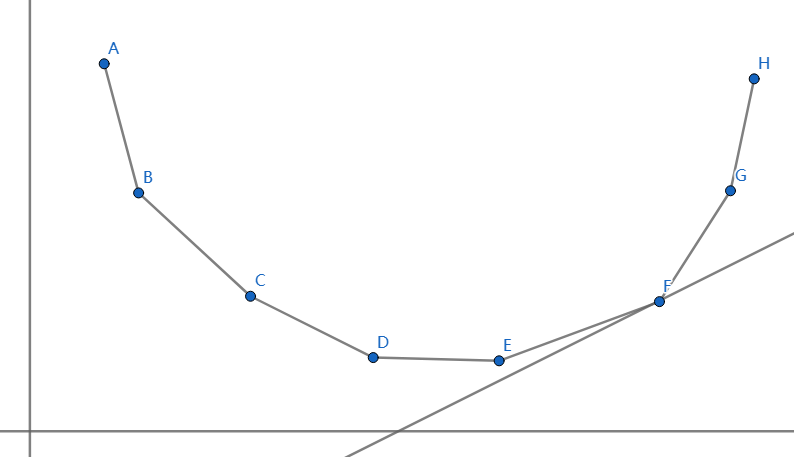
\(val(a)=((\sum_{i=1}^na_i)+1)^2\),\(f(m)\) 为凹函数,考虑 wqs 二分。
二分答案后直接斜率优化 DP 即可,顺便记录最优答案的分段次数 \(g_i\),根据 \(g_i\) 与 \(m\) 之间的大小关系计算下一轮的二分范围,具体的细节见代码。
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const LL N=1e6+1;
LL n,m,g[N],f[N],a[N],s[N];
LL calc(LL x,LL y){
return (s[y]-s[x-1]+1ll)*(s[y]-s[x-1]+1ll);
}
#define Y(P) (f[P]+s[P]*s[P]-2ll*s[P])
#define X(P) (s[P])
long double slope(LL x,LL y){
return 1.*(Y(y)-Y(x))/(X(y)-X(x));
}
void solve(LL mid){
static LL q[N],h,t;
f[0]=g[0]=0;q[h=t=0]=0;
for(LL i=1;i<=n;i++){
while(h<t&&slope(q[h],q[h+1])<2ll*s[i])h++;
LL j=q[h];f[i]=f[j]+calc(j+1,i)+mid,g[i]=g[j]+1;
while(h<t&&slope(q[t-1],q[t])>slope(q[t-1],i))t--;
q[++t]=i;
}
}
int main(){
cin>>n>>m;
for(LL i=1;i<=n;i++)
cin>>a[i],s[i]=s[i-1]+a[i];
LL l=0,r=1e18,ans;
while(l<=r){
LL mid=l+r>>1;
if(solve(mid),g[n]<=m)ans=mid,r=mid-1;
else l=mid+1;
}
solve(ans);
cout<<f[n]-ans*m<<'\n';
return 0;
}