分析
遇到难的题都可以考虑一下弱化版。对于这道题,弱化版很简单,就是排序后对应位置的点匹配。那么加入限制后,可能就会需要微调一下(这种微调的想法也是很有价值的)。
考虑什么时候会需要调整,无非就是匹配到了自己的马。既然要调整,那必然会和另一个人的马交换,在这个基础上,还希望距离原来的尽可能近。
不妨设第 \(i\) 个人的最佳匹配为 \(j\) 号马。从直觉上来说,\(i\) 和 \(j\) 的距离不会很大(我们也可以认为,如果它太大了,我就不会做了,所以它一定不大)。这里给出答案,\(|i-j|\le2\)。
既然猜出了性质,我们就来证明一下。
先有两个明显的性质:
-
如果把 \(i\) 号人与其匹配的 \(j\) 号马连边,那么对于与其交叉的边,交换这两条边对应的匹配,结果必然更大。证明列出不等式即可。
-
对应匹配连边后,与其交叉的边的个数至少有 \(|i-j|\) 条。证明可以先画图,发现一条边划分成两部分后人与马的差值为 \(|i-j|\),即这部分匹配必然穿过划分边。
考虑交叉后不能交换匹配的原因,要么交换后 \(i\) 号人匹配了自己的马,要么 \(j\) 号马匹配了对应的人。对于一个人,最多只有两个交叉无法交换,其他的交叉边都必定有一种方法重新匹配。
然后就无法推进了。
这里给出结论。定义一个区间是匹配好的当且仅当最优匹配时,其中的每一个人所匹配的马都在该区间内。那么全局最优的匹配一定是由许多 \(\text{长度}\le3\) 的匹配好的区间构成的。
考虑证明。设有一个 \(\text{长度}>3\) 的无法细分的匹配好的区间。由于人和马是等价的且 \(|i-j|\le2\),则匹配方案一定由以下的形式组成:中间形如 \((B,4)(C,1)\),左右两侧连回内部,枚举所有情况。发现总是有更优匹配方案。
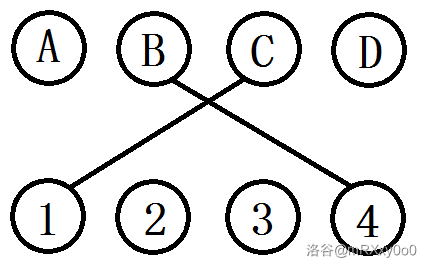
在枚举情况时应当注意到,当它的长度很长时,下方马所对应的人是有重复规律的。所以实际上,可以认为区间长度为 \(4\) 时是其他更长区间的一个缩影,且限制强于其他区间(可以自行手玩一个较长的区间加深理解)。
至此,不带修版本就可以 DP 解决了。对于带修,用动态 DP 维护即可。
代码
#include<bits/stdc++.h>
#pragma GCC optimize(2)
using namespace std;
typedef long long ll;
const int N=3e4+10;
const ll inf=1e18;
int n,q,pos[N];
struct node{
ll v;
int id;
}a[N],b[N];
struct mar{
ll A[3][3];
}B;
struct tree{
int l,r;
mar s;
}tr[N<<2];
inline mar operator*(mar a,mar b){
mar c;
c.A[0][0]=max(a.A[0][0]+b.A[0][0],max(a.A[0][1]+b.A[1][0],a.A[0][2]+b.A[2][0]));
c.A[0][1]=max(a.A[0][0]+b.A[0][1],max(a.A[0][1]+b.A[1][1],a.A[0][2]+b.A[2][1]));
c.A[0][2]=max(a.A[0][0]+b.A[0][2],max(a.A[0][1]+b.A[1][2],a.A[0][2]+b.A[2][2]));
c.A[1][0]=max(a.A[1][0]+b.A[0][0],max(a.A[1][1]+b.A[1][0],a.A[1][2]+b.A[2][0]));
c.A[1][1]=max(a.A[1][0]+b.A[0][1],max(a.A[1][1]+b.A[1][1],a.A[1][2]+b.A[2][1]));
c.A[1][2]=max(a.A[1][0]+b.A[0][2],max(a.A[1][1]+b.A[1][2],a.A[1][2]+b.A[2][2]));
c.A[2][0]=max(a.A[2][0]+b.A[0][0],max(a.A[2][1]+b.A[1][0],a.A[2][2]+b.A[2][0]));
c.A[2][1]=max(a.A[2][0]+b.A[0][1],max(a.A[2][1]+b.A[1][1],a.A[2][2]+b.A[2][1]));
c.A[2][2]=max(a.A[2][0]+b.A[0][2],max(a.A[2][1]+b.A[1][2],a.A[2][2]+b.A[2][2]));
return c;
}
inline bool cmp(node x,node y){
return x.v<y.v;
}
inline ll ask(int t,int x,int y,int z){
return a[t].id==b[t-x].id||a[t-1].id==b[t-y].id||a[t-2].id==b[t-z].id?-inf:a[t].v*b[t-x].v+a[t-1].v*b[t-y].v+a[t-2].v*b[t-z].v;
}
inline mar get(int x){
mar res=B;
res.A[1][0]=res.A[2][1]=0;
res.A[0][0]=(a[x].id==b[x].id?-inf:a[x].v*b[x].v);
if(x>1) res.A[0][1]=max(a[x].id==b[x].id||a[x-1].id==b[x-1].id?-inf:a[x].v*b[x].v+a[x-1].v*b[x-1].v,a[x].id==b[x-1].id||a[x-1].id==b[x].id?-inf:a[x].v*b[x-1].v+a[x-1].v*b[x].v);
if(x>2) res.A[0][2]=max(ask(x,0,1,2),max(ask(x,0,2,1),max(ask(x,1,0,2),max(ask(x,1,2,0),max(ask(x,2,0,1),ask(x,2,1,0))))));
return res;
}
inline void pushup(int u){
tr[u].s=tr[u<<1|1].s*tr[u<<1].s;
}
inline void build(int u,int l,int r){
tr[u]={l,r};
if(l==r){
tr[u].s=get(l);
return ;
}
int mid=l+r>>1;
build(u<<1,l,mid),build(u<<1|1,mid+1,r);
pushup(u);
}
inline void mdf(int u,int x){
if(x>n) return ;
if(tr[u].l==tr[u].r){
tr[u].s=get(x);
return ;
}
int mid=tr[u].l+tr[u].r>>1;
if(x<=mid) mdf(u<<1,x);
else mdf(u<<1|1,x);
pushup(u);
}
int main(){
for(int i=0;i<3;++i){
for(int j=0;j<3;++j){
B.A[i][j]=-inf;
}
}
scanf("%d%d",&n,&q);
for(int i=1;i<=n;++i){
scanf("%lld",&a[i].v);
a[i].id=i;
}
sort(a+1,a+1+n,cmp);
for(int i=1;i<=n;++i){
scanf("%lld",&b[i].v);
b[i].id=i;
}
sort(b+1,b+1+n,cmp);
for(int i=1;i<=n;++i) pos[b[i].id]=i;
build(1,1,n);
while(q--){
int x,y;
scanf("%d%d",&x,&y);
swap(b[pos[x]].id,b[pos[y]].id);
swap(pos[x],pos[y]);
mdf(1,pos[x]),mdf(1,pos[x]+1),mdf(1,pos[x]+2);
mdf(1,pos[y]),mdf(1,pos[y]+1),mdf(1,pos[y]+2);
printf("%lld\n",max(tr[1].s.A[0][0],max(tr[1].s.A[0][1],tr[1].s.A[0][2])));
}
return 0;
}