图像的2D几何变换-526互联

基本概念

齐次坐标

使用 N+1 维坐标来表示 N 维坐标，例如在 2D 笛卡尔坐标系中加上额外变量 w 来形成 2D 齐次坐标系 \((x,y) \Rightarrow (x,y,w)\)。这样做的好处是，在齐次坐标下，图像的几何变换可以利用矩阵的线性变换来表示。

齐次坐标具有规模不变性，同一点可以被无数个齐次坐标表达：\((x,y,1) \Rightarrow (ax,ay,a)\) 齐次坐标转化为笛卡尔坐标可以通过同除最后一项得到。

自由度（Degree of freedom，DOF）是指变换矩阵中变量的个数，代表着可以自由变换的维度。

基础变换

平移（translation）

\[\begin{split}\begin{pmatrix}x^{'}\\y^{'}\\1\end{pmatrix} = \begin{pmatrix} 1 & 0 & t_x \\ 0 & 1 & t_y \\ 0 & 0 & 1 \end{pmatrix} * \begin{pmatrix} x \\ y \\ 1 \end{pmatrix}\end{split} \]

旋转和反射（rotation & reflection）

旋转

\[\begin{split}\begin{pmatrix}x^{'}\\y^{'}\\1\end{pmatrix} = \begin{pmatrix} cos(\phi) & -sin(\phi) & 0 \\ sin(\phi) & cos(\phi) & 0 \\ 0 & 0 & 1 \end{pmatrix} * \begin{pmatrix} x \\ y \\ 1 \end{pmatrix}\end{split} \]

反射

\[\begin{split}\begin{pmatrix}x^{'}\\y^{'}\\1\end{pmatrix} = \begin{pmatrix} cos(\phi) &sin(\phi) & 0 \\ sin(\phi) & -cos(\phi) & 0 \\ 0 & 0 & 1 \end{pmatrix} * \begin{pmatrix} x \\ y \\ 1 \end{pmatrix}\end{split} \]

旋转矩阵和反射矩阵有如下特性;

旋转矩阵和反射矩阵都是正交矩阵
旋转矩阵的行列式值为 +1，反射矩阵的行列值为 -1
旋转矩阵 R(θ) 的逆矩阵为 R(-θ)，反射矩阵的逆矩阵为其本身
旋转矩阵和反射矩阵可以相互转换（注意下面的公式可以看出，旋转可以分解为两次反射来得到，但是反射不能直接通过旋转来得到）
- \(Ref(\theta)Ref(\phi) = Rot(2(\theta-\phi))\)
- \(Rot(\theta)Rot(\phi) = Rot(\theta+\phi)\)
- \(Rot(\theta)Ref(\phi) = Ref(\phi+\theta/2)\)
- \(Ref(\phi)Rot(\theta) = Ref(\phi-\theta/2)\)

缩放（scaling）

各向同性缩放（isotropic scaling）

\[\begin{split}\begin{pmatrix}x^{'}\\y^{'}\\1\end{pmatrix} = \begin{pmatrix} s & 0 & 0 \\ 0 & s & 0 \\ 0 & 0 & 1 \end{pmatrix} * \begin{pmatrix} x \\ y \\ 1 \end{pmatrix}\end{split} \]

广义缩放（scaling）

\[\begin{split}\begin{pmatrix}x^{'}\\y^{'}\\1\end{pmatrix} = \begin{pmatrix} s_x & 0 & 0 \\ 0 & s_y & 0 \\ 0 & 0 & 1 \end{pmatrix} * \begin{pmatrix} x \\ y \\ 1 \end{pmatrix}\end{split} \]

错切（shearing）

错切可以把图形沿着水平或/和垂直方向上进行推移/伸缩，从而可以让一个矩形变成平行四边形。其公式如下

\[\begin{split}\begin{pmatrix}x^{'}\\y^{'}\\1\end{pmatrix} = \begin{pmatrix} 1 & \alpha_x & 0 \\ \alpha_y & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix} * \begin{pmatrix} x \\ y \\ 1 \end{pmatrix}\end{split} \]

如果 \(\alpha_x=0\) 则只有垂直方向拉伸，叫作垂直错切；如果 \(\alpha_y=0\) 则只有水平方向拉伸，叫作水平错切

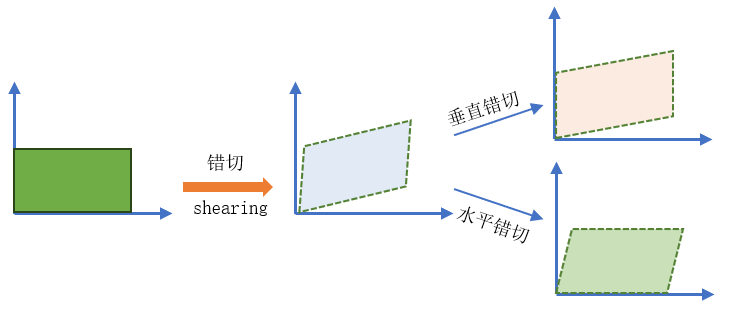
任何错切矩阵的行列式均为 1，即错切是一个面积（3d 中是体积）保持不变的变换 (area/volume-perserving transformation)

复合变换

复合变换可以分解为多个基础变换的叠加，在表达式上体现为变换矩阵的相乘。需要注意的是，正如矩阵相乘不能随意交换矩阵次序一样，相同的基础变换在不同的执行次序下也会产生不同的复合变换结果。

刚体变换 (rigid transformation)

也叫欧几里得变换（Euclidean transformation）

包括旋转变换（rotation）、平移变换（translation）、反射/镜像变换 (Reflection ) 及其组合
3 个自由度：1 个旋转角度 \(\theta\) 和 2 个平移距离 \(\delta x, \delta y\) （这里假设不包括反射，仅包括旋转和平移）
特点
- 保持线段长度、夹角不变（所以可以保持图形的尺寸和形状不变）
表达式

\[x_{3 \times 1}' = \begin{pmatrix} R_{2 \times 2} &t_{2 \times 1} \\ 0^T_{2 \times 1}&1\end{pmatrix} x_{3 \times 1} \]

其中，\(x_{3 \times 1}' = (x1',x2',1)^T\) ；正交矩阵 \(R_{2 \times 2}\) 表征了旋转和反射的影响，如果只有旋转，且旋转角度为 \(\theta\) （根据单位圆中角度定义逆时针为正，下同），则 \(R=\begin{pmatrix} cos \theta & -sin \theta \\ sin \theta & cos \theta \end{pmatrix}\)，如果只有反射，且对称轴的角度为 \(\theta\)， \(R=\begin{pmatrix} cos \theta & sin \theta \\ sin \theta & -cos \theta \end{pmatrix}\)；
列向量 \(t_{2 \times 1} = (\delta x, \delta y)^T\) 表征了旋转的影响；\(0_{2 \times 1}\) 为 0 的二维列向量，其转置为二维行向量。

关于刚体变换是否包含反射的问题？wiki

从刚体变换的直观定义上（保持形状和尺寸不变）来说，刚体变换应该是包括反射的。但是在一些更严格的定义中，会同时要求刚体变换在欧式空间保持 handedness，此时会把反射排除在外，因为反射是镜像变换，会把左手位和右手位颠倒。这种不包括反射的刚体变换定义也叫作 proper rigid transformation、rototranslation，而包括反射的刚体变换叫作 improper rigid transformation。

proper rigid transformation 可以分解为 rotation + translation；improper rigid transformation 可以分解为 improper rotation + translation 或者一系列反射。（improper rotation 也叫 rotation-reflection, rotoreflection, rotary reflection，指的是“沿着某个轴的旋转 + 在垂直这个轴的平面内的反射”）

简单来说，刚体变换是否包括反射需要看具体场合。另外，如果包含了反射，那么刚体变换的自由度应该有 4 个，即旋转角度、反射对称轴的角度、x 方向平移量和 y 方向平移量。

相似变换 (similarity transformation)

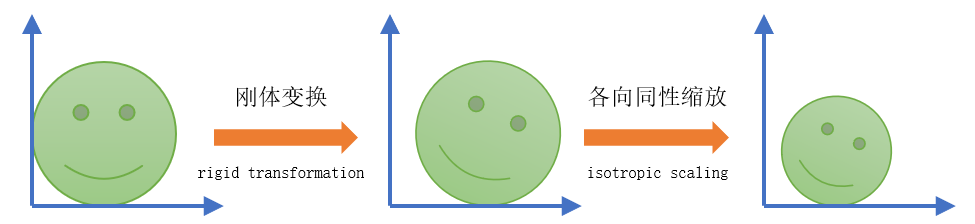
相比刚体变换增加了各向同性缩放变换（isotropic scaling）
4 个自由度，比刚体变换多了一个缩放因子
特点
- 保角性：保持角度不变
- 保持距离比：保持线段之间长度的比值不变
表达式

\[x_{3 \times 1}' = \begin{pmatrix} sR_{2 \times 2} &t_{2 \times 1} \\ 0^T_{2 \times 1}&1\end{pmatrix} x_{3 \times 1} \]

\(s\) 为缩放尺度，标量。

仿射变换 (affine transformation)

仿射变换是在相似变换的基础上多了错切变换&广义缩放。相似变换具有单一旋转因子和单一缩放因子，仿射变换具有两个旋转因子和两个缩放因子。
6 个自由度：比相似变换多一个旋转因子，一个缩放因子
特点
- 平直性：
- 图像经过仿射变换后，直线仍然是直线
- 平行性：图像在完成仿射变换后，平行线仍然是平行线。
- 直线上各点比例保持不变（如中点仍是中点）
表达式

\[x'_{3 \times 1} = \begin{pmatrix}A_{2 \times 2}&t_{2 \times 1} \\ 0^T_{2 \times 1}&1\end{pmatrix} x_{3 \times 1} \]

A 为 2×2 的非奇异矩阵,可被分解为如下: \(A = R(\theta)R(-\phi)DR(\phi)\)

其中 \(R(\theta) R(\phi)\) 为旋转矩阵，D 为对角阵 \(D = \begin{pmatrix} \lambda_1 & 0 \\ 0 & \lambda_2 \end{pmatrix}\)

\(\lambda_1 和 \lambda_2\) 可以看做两个方向的缩放比。

投影变换 (projective transformation)

也叫作透视变换（perspective transformation）、单应性变换（homography ）、直射变换（collineation）

投影变换将图像投影到一个新的视平面，是二维到三维再到另一个二维 (x', y') 空间的映射
投影变换是齐次坐标下非奇异的线性变换，即可以用矩阵运算 \(x^{'}= Hx\) 来表示，其中 \(H\) 为非奇异矩阵。需要注意的是，在非齐次坐标系下，投影变换是非线性的。
8 个自由度，比仿射变换多 2 个自由度
特点
- 保持三点共线
表达式：

\[x'_{3 \times 1} = \begin{pmatrix}A_{2 \times 2}&t_{2 \times 1} \\ V^T_{2 \times 1}&v\end{pmatrix} x_{3 \times 1} \]

其中 \(V_{2 \times 1} = (v_1,v_2)^T\)；\(v\) 标量常数，一般可设置为 1.

Tips

投影变换有 8 个自由度，其变换矩阵的计算最少需要 4 对配对点
当投影变换矩阵的最后一行为（0，0，1）时，变换就为仿射变换，在仿射的前提下，当左上角 2×2 矩阵正交时为欧式变换，左上角矩阵行列式为 1 时为定向欧式变换。所以射影变换包含仿射变换，而仿射变换包含欧式变换。
投影变换的特点是可以实现透射效果，即满足近大远小的视觉特征。

Reference

几何

图像

opencv-python几何图像opencv