解析解
最小二乘法求极值
对于\(p\)维数据,多元线性回归使用\(p\)元线性函数\(y = a_1x_1 + a_2x_2 + \cdots +a_px_p + a_0\)拟合真实数据分布。此时预测数据\(\hat y\)与真实数据\(y\)的均方误差\(MES = \frac{1}{n} \sum_{i=1}^{n}(\sum_{j=1}^{p}a_{j}x_{ij} + a_{0}-y_i)^2\)。
如果把预测数据\(\hat y\)写成矩阵形式\(\hat Y = XA\),其中
\(X = \begin{pmatrix}
1 & x_11 & x_12 & \cdots & x_{1p} \\
1 & x_21 & x_22 & \cdots & x_{2p} \\
\vdots & \vdots & \vdots & \ddots & \vdots\\
1 & x_n1 & x_n2 & \cdots & x_{np} \\
\end{pmatrix}\)\(A = \begin{pmatrix}
a_0 & a_1 & \cdots & a_p
\end{pmatrix}
^{T}\)
那么,均方误差\(MSE = \frac{1}{n}\begin{Vmatrix}
\hat Y - Y
\end{Vmatrix}
^2\) ,其中\(\hat Y = XA\),\(Y = \begin{pmatrix}
y_1 & y_2 & \cdots & y_n
\end{pmatrix}
^T\)。
此时,我们的目标函数是\(\hat A = \underset{A}{\arg\min}\,MES\),其中\(\frac{1}{n}\)对结果不产生影响,为了方便后面计算我们重新定义\(\underset{A}{\arg\min}\,MES\)中的\(MES = \begin{Vmatrix}
\hat Y - Y
\end{Vmatrix}
^2\)。
对\(MES\)化简可得
\(\begin{aligned}
MES &= \begin{pmatrix}\hat Y-Y\end{pmatrix}^T\begin{pmatrix}\hat Y-Y\end{pmatrix} \\
&= A^TX^TXA - 2A^TX^TY + Y^TY
\end{aligned}\)
我们通过对\(A\)求偏导,令偏导数等于0。
\(\frac{\partial MES}{\partial A} = 2X^TXA - 2X^TY = 0
\\
\Rightarrow
X^TXA = X^TY\)
最终解得
\(\hat A = (X^TX)^{-1}X^TY\)
极大似然估计法
数据集:\(X = \begin{pmatrix}
1 & x_11 & x_12 & \cdots & x_{1p} \\
1 & x_21 & x_22 & \cdots & x_{2p} \\
\vdots & \vdots & \vdots & \ddots & \vdots\\
1 & x_n1 & x_n2 & \cdots & x_{np} \\
\end{pmatrix}\)参数向量:\(A = \begin{pmatrix}
a_0 & a_1 & \cdots & a_p
\end{pmatrix}
^{T}\)标签:\(Y = \begin{pmatrix}
y_1 & y_2 & \cdots & y_n
\end{pmatrix}
^T\)
我们令\(X\)的第\(i\)行构成的列向量为\(x_i\)
我们做如下假设:
预测数据\(\hat y\)与真实数据\(y\)的误差\(\epsilon \sim N(0, \sigma^2)\)。因为\(y = A^Tx + \epsilon\),所以\(y \sim N(A^Tx, \sigma^2)\)。
密度函数\(f(y) = \frac{1}{\sqrt{2\pi}\sigma}e^{\frac{(y-A^Tx)^2}{2\sigma^2}}\),根据极大似然估计法估计参数\(A\)的值。
似然函数\(L(A) = \prod_{i = 1}^{n}\frac{1}{\sqrt{2\pi}\sigma}e^{\frac{(y_i-A^Tx_i)^2}{2\sigma^2}}\)
取对数后得到
\(\ln{L(A)} = \sum_{i = 1}^{n}\ln{\frac{1}{\sqrt{2\pi}\sigma}} + \sum_{i = 0}^{n}\ln{e^{\frac{(y_i-A^Tx_i)^2}{2\sigma^2}}}\)\(\Rightarrow\)\(\underset{A}{\arg\max}\,\ln{L(A)} = \underset{A}{\arg\min}\,\sum_{i = 0}^{n}(y_i-A^Tx_i)^2\)
我们不难推导出\(\sum_{i = 0}^{n}(y_i-A^Tx_i)^2 = \begin{Vmatrix} XA - Y \end{Vmatrix}
^2\),推导过程如下:
\(\sum_{i = 0}^{n}(y_i-A^Tx_i)^2 = \sum_{i = 0}^{n}(A^Tx_i - y_i)^2\)
上式根据求和符号逐项拆开可得
\((A^Tx_1 - y_1, A^Tx_2 - y_2,...,A^Tx_n - y_n)(A^Tx_1 - y_1, A^Tx_2 - y_2,...,A^Tx_n - y_n)^T\)
左边一项可以写成\(A^TX^T - Y^T = (XA-Y)^T\),左边一项是左边项的转置,故右边项为\((XA-Y)\)
所以\(\sum_{i = 0}^{n}(y_i-A^Tx_i)^2 = (XA-Y)^T(XA-Y)= \begin{Vmatrix} XA - Y \end{Vmatrix}
^2\)
综上所述\(\underset{A}{\arg\max}\,\ln{L(A)} = \underset{A}{\arg\min}\,\begin{Vmatrix} XA - Y \end{Vmatrix}
^2\),求解过程过程和最小二乘法求极值法一致
几何角度
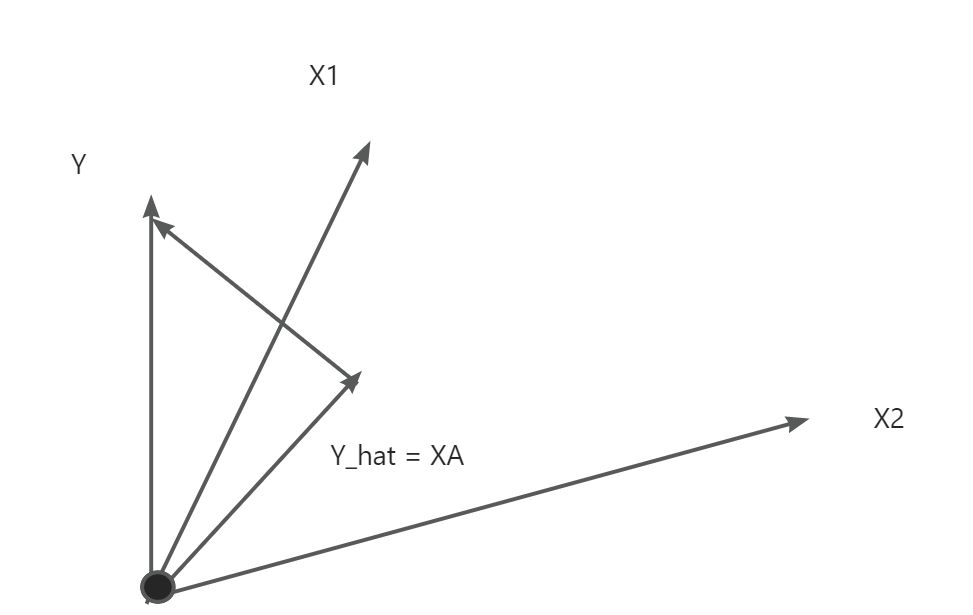
对于预测向量\(\hat y = a_0 + a_1x_1 + a_2x_2 + \cdots +a_px_p\),可以看成\(p+1\)个列向量\(1, x_1, x_2, ..., x_p\)的线性组合,系数构成稀疏向量A。实际的标签向量\(Y\)为\(p+1\)个列向量张成的空间外的一个向量。
我们的目标是在\(p+1\)个列向量张成的空间中寻求出\(\hat Y\),使得\(Y\)和\(\hat Y\)的距离最小。显然当\(Y - \hat Y\)与\(p+1\)个列向量张成的空间垂直时\(Y\)和\(\hat Y\)的距离最小。
此时\((1, x_1, x_2, ..., x_p)^T(Y - \hat Y) = X^T(Y - \hat Y) = 0\)
即\(X^T(Y - XA) = 0\)\(\Rightarrow\)\(X^TY - X^TXA = 0\)⇒\(A = (X^TX)^{-1}X^TY\)
梯度下降优化求解
线性回归系数解析解\(A = (X^TX)^{-1}X^TY\),可以看到对于解析解必须满足数据矩阵\(X\)是列满秩的,否则不能求出\(X^TX\)的逆矩阵。
有时我们并不需要求出解析解,此时我们就可以使用梯度下降的方法优化损失函数,求解系数向量A。
我们有损失函数\(L = \frac{1}{n}\begin{Vmatrix}
\hat Y - Y
\end{Vmatrix}
^2\),使用梯度下降法,不断更新A的值。