526互联

[ABC232E] Rook Path

发布时间 2024-01-07 16:33:42作者: cloud_eve

题意

在象棋棋盘上有一个车，它的位置是 \((x1,y1)\)，求车从此处到达 \((x2,y2)\) 有多少种情况。

思路

明显的组合数学与 DP 题。

最最最先，一定要明确一个概念，车可以横向或竖向移动到当前列或行的任意一个（除去它本身现在的位置），但不可以斜着移动。

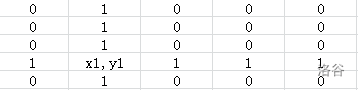
如图所示，\((x1,y1)\) 是车当前的位置，标注 \(1\) 的位置是车可以一步到达的，而标注 \(0\) 的位置则意味着不可以一步到达。

考虑暴力 DP。设 \(dp_{x, y, k}\) 表示进行了 \(k\) 次操作后车走到 \((x, y)\) 的方案数。
状态转移方程为：

\[dp_{x, y, k} = \sum_{1 \le i \le H,i \neq x} dp_{i, y, k - 1} + \sum_{1 \le i \le W,i \neq y} dp_{x, j, k - 1} \]

最终答案为 \(dp_{x2, y2, k}\)。

但这样高达 \(O(kH^3)\) 的优秀时间复杂度，再水的数据都明显过不了。
考虑优化。

我们可以设四个集合，分别表示：

  • \(S_{0, 0}\) 表示与车同行同列（就是车的位置）的点的集合；
  • \(S_{0, 1}\) 表示与车同行不同列的点的集合；
  • \(S_{1, 0}\) 表示与车同列不同行的点的集合；
  • \(S_{1, 1}\) 表示与车不同行不同列的点的集合。

可以表示为：
\(S_{0, 0} = {(x, y) \mid x = x1, y = y1}\)；
\(S_{0, 1} = {(x, y) \mid x = x1, y \neq y1}\)；
\(S_{1, 0} = {(x, y) \mid x \neq x1, y = y1}\)；
\(S_{1, 1} = {(x, y) \mid x \neq x1, y \ neq y1}\)。

观察四个集合，可以看出当 \(a, b \in {0, 1}\) 且 \((x1, y1)(x2, y2) \in S_{a, b}\) 时，\(dp_{x1, y1, k} = dp_{x2, y2, k}(0 \le k \le K)\)。
当 \(k\) 相同时，同一个集合内的所有点的 \(dp\) 值是相同的。

所以不妨设：

\[f_{n, m, k}(n, m \in {0, 1}) = \sum_{(x, y) \in S_{a, b}} dp_{x, y, k} \]

那么 \(f\) 的边界条件也就很好处理了。分别是：

  1. \(f_{0, 0, 0} = 1\)；
  2. \(f_{0, 1, 0} = 0\)；
  3. \(f_{1, 0, 0} = 0\)；
  4. \(f_{1, 1, 0} = 0\)。

现在就可以推导转移方程了。方便起见，可以先分情况讨论：

  • \(x1 = x2\) 且 \(y1 = y2\)：\(ans = f_{0, 0, k}\)；
  • \(x1 = x2\) 且 \(y1 \neq y2\)：\(ans = \frac{f_{0, 1, K}}{W - 1}\)；
  • \(x1 \neq x2\) 且 \(y1 = y2\)：\(ans = \frac{f_{0, 1, K}}{H - 1}\)；
  • \(x1 \neq x2\) 且 \(y1 \neq y2\)：\(ans = \frac{f_{0, 1, K}}{(W - 1) \times (H - 1)}\)。

那么转移方程就应为：

  • \(f_{0, 0, k} = f_{0, 1, k - 1} + f_{1, 0, k - 1}\)；
  • \(f_{0, 1, k} = (W - 1) \times f_{0, 0, k - 1} + (W - 2) \times f_{0, 1, k - 1} + f_{1, 1, k - 1}\)；
  • \(f_{1, 0, k} = (H - 1) \times f_{0, 0, k - 1} + (H - 2) \times f_{1, 0, k - 1} + f_{1, 1, k - 1}\)；
  • \(f_{1, 1, k} = (W - 1) \times f_{0, 1, k - 1} + (H - 1) \times f_{1, 0, k - 1} + (W + H - 4) \times f_{1, 1, k - 1}\)。

得解。

代码

除法需要使用乘法逆元。

所用的函数请务必使用 long long！
不然就会：R.I.P。

#include <bits/stdc++.h>
#define int long long
using namespace std;
const int mod = 998244353, N = 1e7 + 5;
int n, m, k, x, y, xx, yy;
int ans;
int f[2][2][N];
int inv(int x) {
	return x == 1 ? 1 : (mod - mod / x) * inv(mod % x) % mod;
}
signed main() {
	scanf("%lld%lld%lld", &n, &m, &k);
	scanf("%lld%lld%lld%lld", &x, &y, &xx, &yy);
	f[0][0][0] = 1;
	for (int i = 1; i <= k; i++) {
		f[0][0][i] = (f[0][1][i - 1] + f[1][0][i - 1]) % mod;
		f[0][1][i] = ((m - 1) * f[0][0][i - 1] % mod + (m - 2) * f[0][1][i - 1] % mod + f[1][1][i - 1] % mod + mod) % mod;
		f[1][0][i] = ((n - 1) * f[0][0][i - 1] % mod + (n - 2) * f[1][0][i - 1] % mod + f[1][1][i - 1] % mod + mod) % mod;
		f[1][1][i] = ((n - 1) * f[0][1][i - 1] % mod + (m - 1) * f[1][0][i - 1] % mod + (n + m - 4) * f[1][1][i - 1] % mod + mod) % mod;
	}
	if (x == xx && y == yy) ans = f[0][0][k];
	else if (x == xx && y != yy) ans = f[0][1][k] * inv(m - 1) % mod;
	else if (x != xx && y == yy) ans = f[1][0][k] * inv(n - 1) % mod;
	else ans = f[1][1][k] * inv((n - 1) * (m - 1) % mod) % mod;
	printf("%lld\n", ans);
	return 0;
}