拓扑微分几何深度学习技术
数学与AI:AI的拓扑几何基础
本次讲座邀请了纽约州立大学石溪分校计算机系帝国创新教授顾险峰老师。

顾险峰:
1994年于清华大学获得计算机科学学士学位,2002年于哈佛大学获得计算机科学博士学位,师从国际著名微分几何大师丘成桐先生。顾博士目前为纽约州立大学石溪分校计算机系帝国创新教授,与丘先生创立了计算共形几何跨领域学科,将现代拓扑与几何理论与计算机科学相结合,广泛应用于计算机图形学、视觉、网络、CAD/CAE、医学图像、计算力学等工程和医疗等领域。近期,顾博士与合作者们将微分几何、蒙日-安培方程与最优传输理论相结合,开发了最优传输映射的几何变分算法,应用于可解释深度学习等领域。顾博士发表了300多篇学术论文,7部学术专著,其发明的调和映照、Abel微分、曲面Ricci流、几何最优传输映射等算法被广泛应用于很多工业医疗等领域。顾博士曾经获得美国国家自然科学基金CAREER奖,中国国家自然科学基金海外杰青,晨兴应用数学金奖等。
深度学习方法在很多领域取得很大成功,但是深度学习的理论基础依然薄弱。这里从几何拓扑的观点出发,分析深度学习的理论基础,力图回答这一领域的基本问题:深度学习究竟在学习什么?深度学习如何进行学习?学习效果如何?从几何角度而言,深度学习本质上是在学习高维背景空间中低维数据流形上的概率分布。流形结构的学习基于Whitney流形嵌入理论,由编码解码器来万有逼近;概率分布的学习依赖于最优传输理论,在Wasserstein空间中做变分优化;目前深度学习模型设计有内在缺陷,基本问题不可避免,例如模式坍塌。基于最优传输理论的几何观点,揭示模式坍塌的根本原因,提出基于几何变分的学习模型,提高计算准确性、稳定性和效率。
深度学习在实践中非常成功,但是其理论基础一直没有被建立起来。先来看三个问题:深度学习究竟在学什么?深度学习是如何学习的?深度学习是否真正学会?
现在的深度神经网络经常有数十亿个参数,其容量足够可以完全记住教给它的所有样本,那么它是否真正提炼出了一些新的知识,还是单纯记忆了所有训练样本?它的学习效果怎么样,它是否真地学会了教它的所有内容,还是不得不遗忘部分内容?准备从数学角度回答这三个基本问题。
Manifold Distribution Principle (流形分布定则)
Helmholtz Hypothesis (亥姆霍兹假设)
深度学习究竟在学什么?在脑神经科学中,有许多研究成果,其中一个叫做Helmholtz假设。这是说人类视觉中枢通过观看自然界的各种景象会产生相应的概念,这些概念都被记录在特定的神经元之中,从而形成某种表示。
用数学语言来讲的话,人脑视觉中的每个概念都可以归结于物理世界中的一个数据集,不同的概念实际上对应着不同的概率分布。
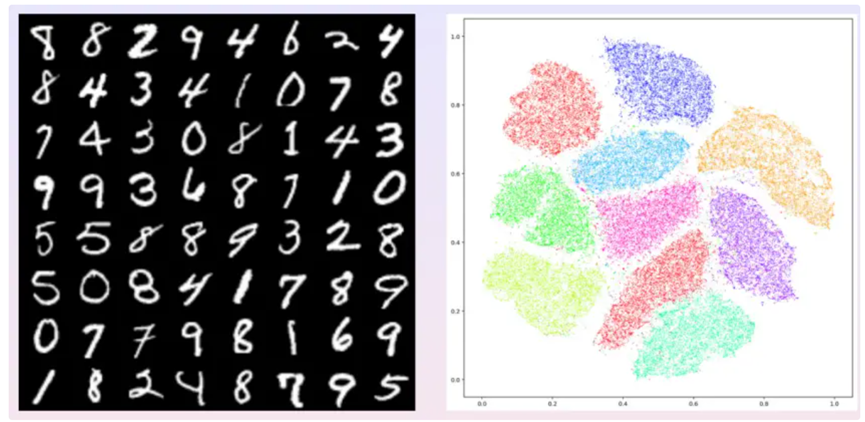
例如上图,左帧显示了Yann Lecunn收集的手写体数字图片,这里的概念是手写体数字,其对应的数据集就是所有的手写体数字图片。LeCunn把收集的这些数据集图片缩放成统一的比例,例如图像解析率为28*28,每个像素灰度取值为0或1。可以将每张图片看成是28*28维空间中的一个点,由此得到一个784维的背景空间,背景空间中的每个点代表一个图像。大量的图像是没有物理意义的,绝大多数有意义的图像也并不代表手写体数字,只是非常独特的一些图像才代表手写体数字。所有手写体图像在这784维的图像空间中构成一个点云,这个点云的维数是非常低的,称之为手写体数字对应的数据流形。
需要区分一下概念,有一个784维的背景空间,其中有一个特殊的点云,上面的每个点代表一个手写体数字,这个点云是数据流形。数据流形的维数是多少呢?Hinton发明了t-SNE算法将点云映射到二维平面上,即隐空间或者特征空间上。这个映射是可逆的连续双射,即拓扑同胚。这也就是说如果在隐空间中任取一点,它可以返回到数据流形上的原像,即生成一张图片。这意味着手写体数字的点云只有两维,即数据流形是两维的曲面,这张曲面嵌入在784维的背景空间之中。
深度学习的第一步就是将这个曲面打到二维平面上,把每一个图像变成一个特征向量,从而实现了降维。手写体数字从0到9共有10个数字,所以其在二维隐空间或者特征空间中有10个团簇。如上图中的右帧,每个团簇用不同的颜色来表示,各自代表一个手写体数字。每个手写体数字代表不同的概率分布,实际上在二维曲面上的分布是不均匀的。
由此可以看出,深度学习所学习的概念最终是由概率统计的语言来描述的,某种特定的概率分布,这个概率分布是定义在高维背景空间中的某个低维数据流形上面的。
Encoding (编码)



知道深度学习中的生成模型,模拟的是人类的想象力。在特征空间随便找一个采样点并映射回数据流形上,流形上每个点就是一幅图像,由此得到了想象出来的一幅图像。采样点需要精确选取。如上图所示,在特征空间设置一个10*10的采样矩阵,每个采样点对应右侧的一幅图像。可以看到如果采样点落在概率分布的支集(support)之内,生成的数字图像非常清晰;如果采样点落在支集之外,生成的数字图像比较模糊,并且并介于两个数字之间,难以辨认。因此在想象的时候,采样点需要落在有意义的区域之内,即落在支集之内;采样点落在支集之外,所造成的模糊现象被称为模式混淆。
General Model (通用模型)
可以用数学语言来描述,背景空间是一个图像空间,图像空间的维数就等于每张图像上像素的个数。某一自然概念对应的数据集就是图像空间中的一个点云,这个点云构成一个低维的流形,被称之为数据流形。在数据流形上选取一个开集,并通过编码映射到特征空间(隐空间)之中。
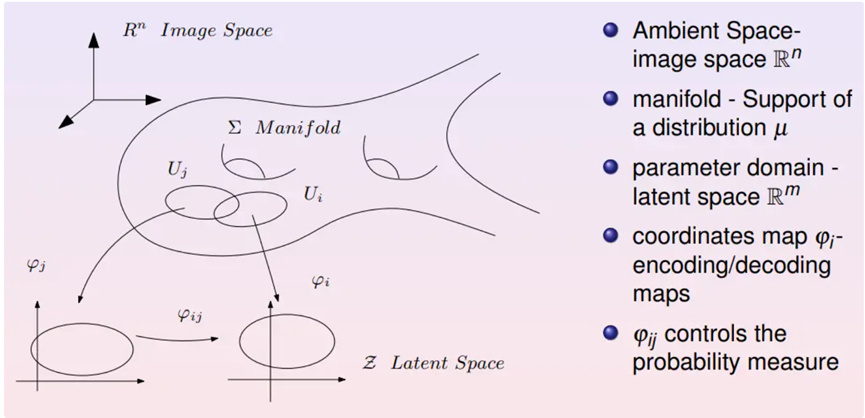
反之,从特征空间回到数据流形的映射被称为解码映射。所以编解码的过程相当于为流形建立了一个局部坐标。由此,可以把深度学习的语言翻译成拓扑语言。
Low Dimensional Example (低维算例)
如图所示,假设二维弥勒佛曲面嵌入在三维欧氏空间之中,曲面上存在一个均匀分布。对于深度学习而言,第一步就要实现降维,计算由三维曲面到二维平面的映射。

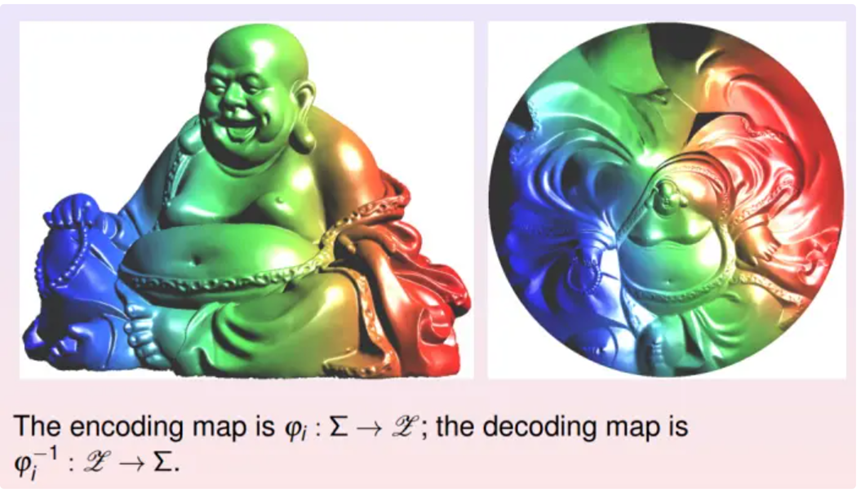

降维的过程被称为编码,逆过程被称为解码。这里显示了两种编码映射,它们都将弥勒佛曲面映到平面单位圆盘上。第一种是基于黎曼映照的保角变换,第二种是基于最优传输的保面元映射。
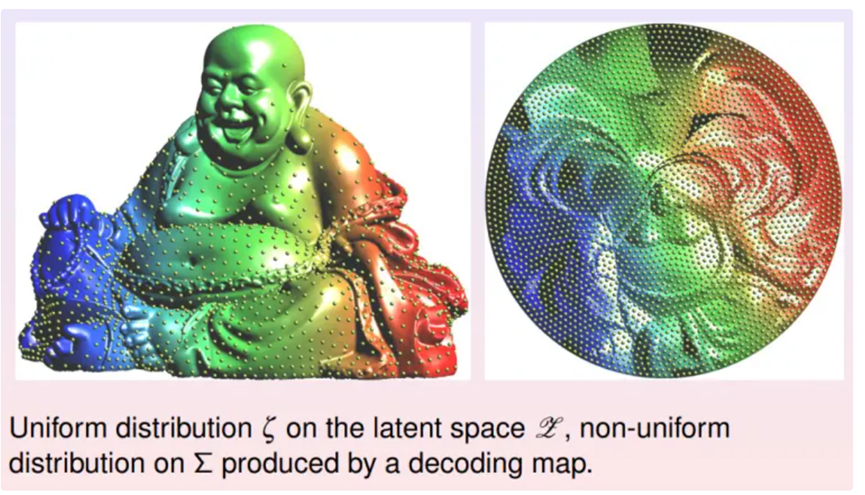
在黎曼映射的平面像上均匀采样,在将采样点拉回到三维曲面上。看到曲面上采样点分布不再均匀,这意味着这种编码映射破坏了数据流形上本来的概率分布。

在最优传输映射的平面像上均匀采样,在将采样点拉回到三维曲面上。看到曲面上采样点分布依然均匀,这意味着这种编码映射保持了数据流形上本来的概率分布。
这也显示了深度学习的终极目的:第一是学会模型的拓扑结构,实现降维并将其映射到特征空间上;第二要保留数据流形上本来的概率分布,在特征空间上的概率分布保持原来流形上的真实分布。
Central Tasks for DL (深度学习的中心任务)
深度学习究竟想学什么?主要是有两个中心任务:
(1)数据流形的拓扑结构
(2)数据流形上的概率分布
Generative Model Framework (生成模型的框架)

知道有很多的生成模型,这些模型的框架如图所示,上面一行显示了学习流形结构的过程,下面一行是学习概率分布的过程。在上行中,编码映射将手写体数字流形映射到特征空间,将流形上的概率分布映射到隐空间上的概率分布;解码映射将隐空间映回数据流形。在下行中,最优传输映射将长方形内的均匀分布映射到隐空间中的数据分布,这里最优传输映射是某一凸函数的梯度映射,此凸函数被称为是Brenier势能。
Human Facial Image Manifold (人脸图像流形)

在工程实践中,经常要生成许多人脸图像。这里对应的概念就是人脸图像,每张图像包含上百万像素,因此图像空间维数很高。在图像空间中的每个点代表一幅图片,所有人脸图像构成点云,即弯曲的数据流形。经过大幅度的降维,将人脸图像数据流形映射到隐空间上,不同类型的人脸表示成流形上不同的概率分布,深度生成模型的核心就是学习人脸图像的概率分布。
Manifold view of Generative Model
(流形观点下的生成模型)

在特征空间生成一个白噪声,均匀分布或者高斯分布,然后将其变换成特征空间中的数据分布。这样可以在特征空间产生随机采样点,其分布符合数据分布,在将隐空间的随机采样带映射回数据流形上,得到数据流形上的一个采样点,即为随机生成的人脸图像。
Manifold view of Denoising
(流形观点下的去噪)
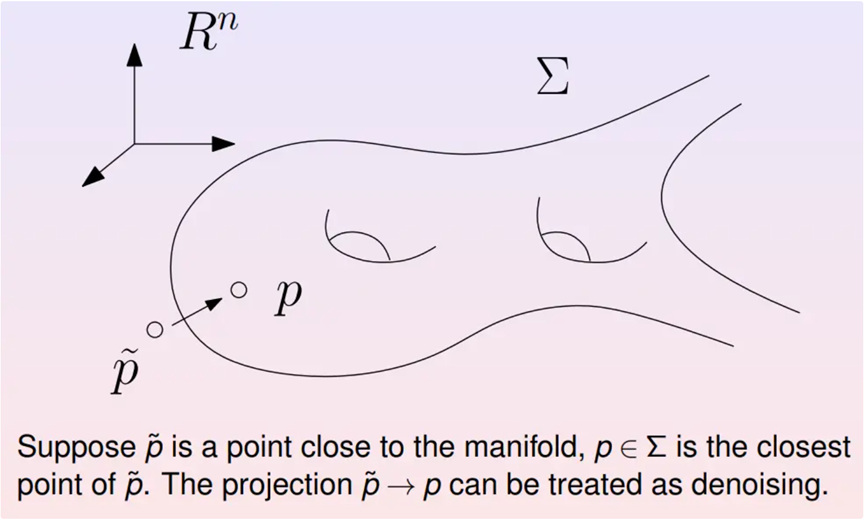
假如想对图像进行去噪处理。如果用经典方法,第一步需要进行傅里叶分解将图像变换到频域,然后进行低通频滤波,滤除高频噪声,最后进行傅里叶逆变换。这种方法是普适的,而深度学习则是另一种思路。先用干净的图像训练出数据流形。带有噪音的图像被视为数据流形附近的点。将其投影到流形上,则流形上的垂足就是去除噪音的图像。如此就实现了图像的去噪处理,下面是相关的实验结果。
Manifold view of Denoising
(流形观点下的图像去噪)

给人脸图像加上白噪声并用上述提到的方法进行投影。发现这种方法相比传统方法仍旧存在缺点,即需要事先知道所处理图像的类别。另一方面,深度学习方法可以将大量的先验知识包含在数据流形之中,所以所实现的去噪效果要优于传统方法。
Manifold Learning
(流形学习)
Topological Theoretic Foundations
(拓扑理论基础)
深度学习如何学习流形的结构呢?这涉及一些拓补学上的定理。
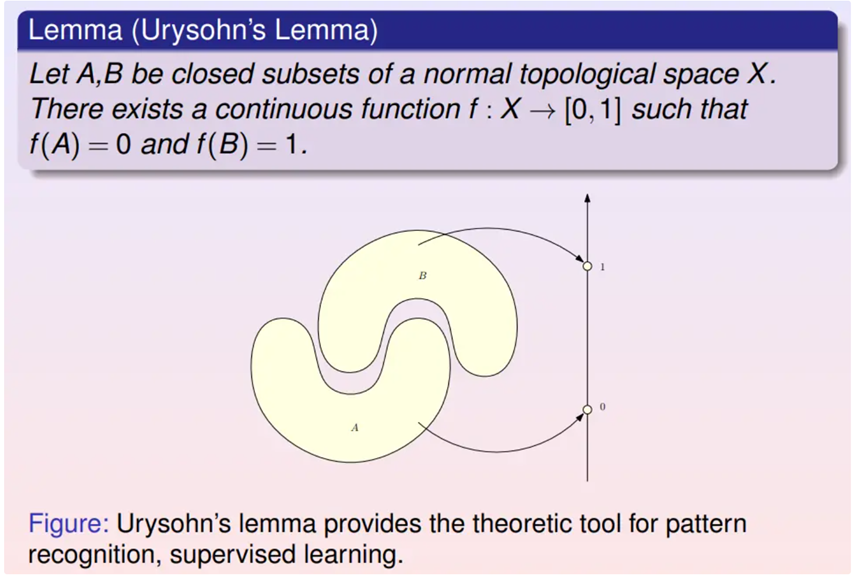
进行模式识别的时候,每一类数据样本其实都是高维空间中的点云,不同类样本是不同的团簇,两个团簇可以用两个闭集覆盖。上述Urysohn定理表明了所需识别映射的存在性:即在一般的拓扑空间里肯定能找到一个连续映射,把第一个闭集映射成0,把第二个闭集映射成1。对于分类判别器而言,算法的核心就是求解这个映射。
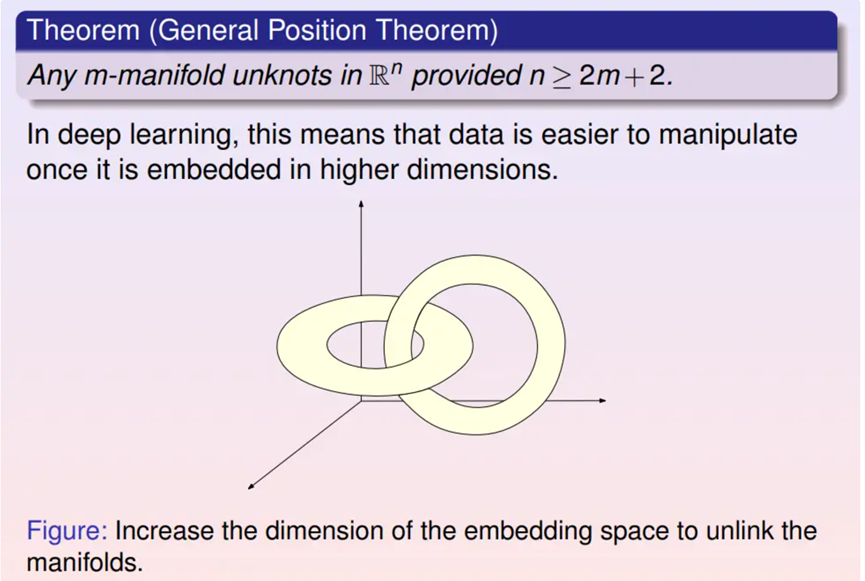
一般而言,数据流形的拓扑结构可能非常复杂,彼此有嵌套、链接和扭曲。
考虑流形在欧氏空间中的嵌入,一般位置定理断言如果欧氏空间的维数足够高,那么流形的嵌入可以将扭结打开使其不再自嵌套。因此,在深度网络模型中,前面几层的宽度逐步增加,从而提高嵌入空间的维数。
Whitney Manifold Embedding
(Whitney流形嵌入)

Whitney流形定理是说任意给一个m维拓扑流形,可以将其嵌入在欧式空间中,欧氏空间的维数大约是流形维数的两倍。现在很多深度学习的算法本质上就是Whitney定理的实现。Whitney定理的证明需要先用一族开集覆盖流形,将每个开集嵌入到欧氏空间,然后用所谓的单位分解把局部嵌入整体粘起来得到一个全局嵌入。这时嵌入空间的维数等于流形的维数乘以开集的个数,在将嵌入的流形依次向低维线性子空间投影,直至无法进一步投影,这时子空间的维数等于流形维数的两倍。
Universal Approximation
(万有逼近)

深度神经网络具有万有逼近的性质,即只要给定一个连续映射,给定任意的逼近精度,都存在某个深度神经网络来进行逼近。这个性质的理论基础实际上是来自Hilbert 第13问题:任意一个多变元的连续函数,都可以由两个单变元函的有限复合以任意精度来逼近。可以看到深度学习的逼近理论大多是基于这个定理。
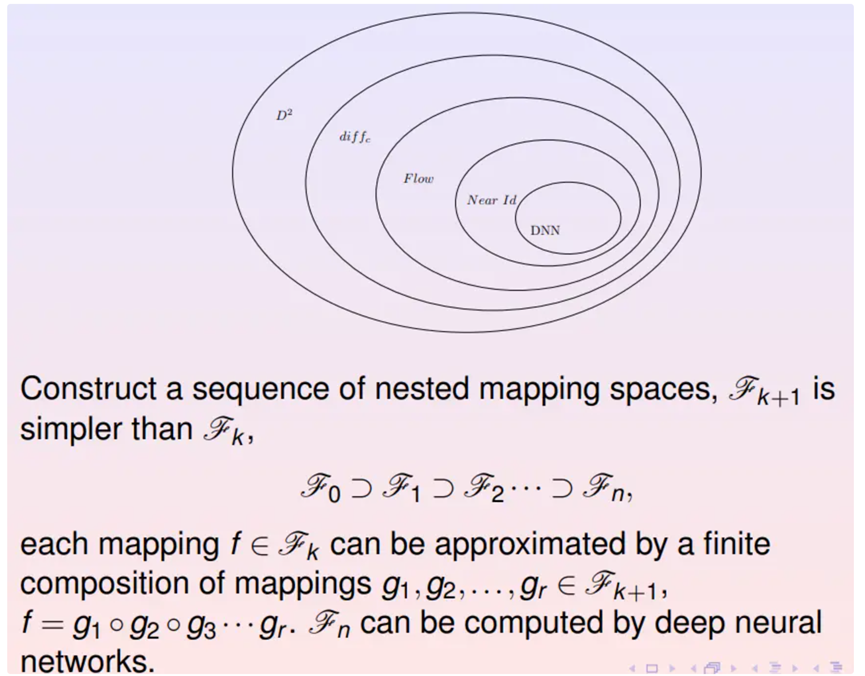
目前基于流的深度学习模型日益普遍,这是基于变换群的逼近原理。希望逼近二阶光滑的可微变换群,其中有个无穷光滑的微分同胚子群,子群中的有限元素的乘积可以逼近原来大群中的任意元素。
类似的,无穷光滑的微分同胚群中存在一个基于流的子群,即由流速场诱导的变换子群;这个流变换子群存在更小的子群,即靠近恒同变换的子群。如此得到一系列嵌套的子群用子群中的有限复合来逼近原来大群中的任何一个元素。而最终的子群足够简单,可以用深度神经网络来精确表达。
Autoencoder
(自动编码器)

这里考察最简单的编码解码网络:自动编码器。以刚刚提到的手写体数字识别为例,编码器的输入样本是28*28的手写体图像,输出是复制的相同图像,损失函数是使生成图像与输入图像的距离。设计两个对称的网络,前面网络是编码器,后面网络是解码器,中间的瓶颈层代表了隐空间,瓶颈层节点的个数是隐空间的维数。前面网络将输入图像从784维降维两维,实际上相当于一个编码映射,后面网络从两维变回784维,相当于解码映射。训练的目的是得到恒同变换,即编码映射和解码映射彼此互逆,由此编码和解码映射是从数据流形到特征空间的拓扑同胚。
Encoding/Decoding (编码/解码)
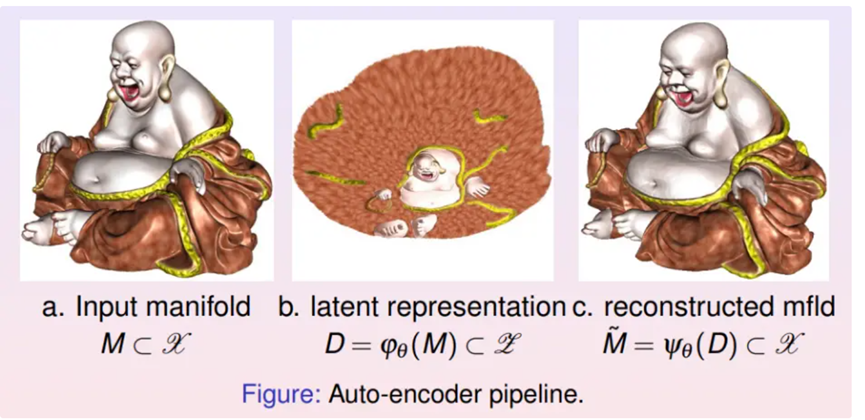
这里举一个简单的例子,用自动编码器学习弥勒佛曲面的拓扑结构。在曲面上均匀采样,将3000个采样点作为自动编码器的输入。编码映射将曲面展平到二维平面上,解码映射将平面像映回到三维空间。看到重建的曲面和初始曲面非常接近,所有精细的几何细节都被完美保持。这证明了编码解码映射实现了拓扑同胚。
ReLU DNN (ReLU深度神经网络)

可以用ReLU DNN实现这个映射,ReLU DNN是线性变换与ReLU变换的多级复合,整体是一个分片线性映射。
Activated Path (激活路径)

如果给定一个训练样本,它会激活神经网络中的特定神经元,被激活的神经元构成网络中的通路,被称为是激活路径。
Cell Decomposition (胞腔分解)

如果有两个训练样本,它们的激活路径是相同的,那么认为它们彼此等价。这样,将空间按照等价分类,得到输入空间的胞腔分解。
Piecewise Linear Mapping (分片线性映射)
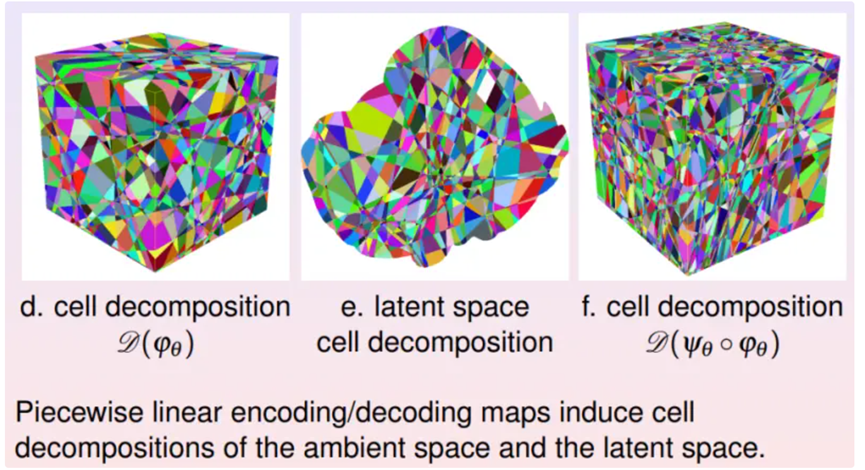
这里显示输入、输出空间和隐空间的胞腔分解,编码映射和解码映射在相应的胞腔间是线性映射,因而整体是分片线性映射。
Learning Capability (学习能力)

给定一个神经网络,该如何定量地衡量其学习能力?可以如下定义深度神经网络的学习能力:神经网络将输入空间进行胞腔分解,胞腔的个数越多,则网络能够表达的映射越非线性。由此,可以考察网络可能产生的所有胞腔分解,用胞腔个数的上限来表达网络的其学习能力。

RL Complexity Upper Bound (复杂度上限)
通过计算几何方法,可以估算其胞腔个数的上限。

RL Complexity of Manifold (流形复杂度)

如何表示学习一个流形的难度呢?观测上图左侧曲线,可以将其向平面进行投影,映射到一条直线段上,并且这个投影是同胚;而右侧曲线无论向任何方向投影都无法同胚映射到直线段上,必须将曲线分成几段,每段分别双射投影到直线段上。一般情形下,需要对流形分片,每片同胚投影到线性空间,所有分解方法中片数的下限定义了流形的复杂度。
Encodable Condition (能够编码的必要条件)

如果能用一个深度神经网络学会一个流形,那么神经网络的学习能力一定要大于等于流形的复杂程度。
Representation Limitation Theorem
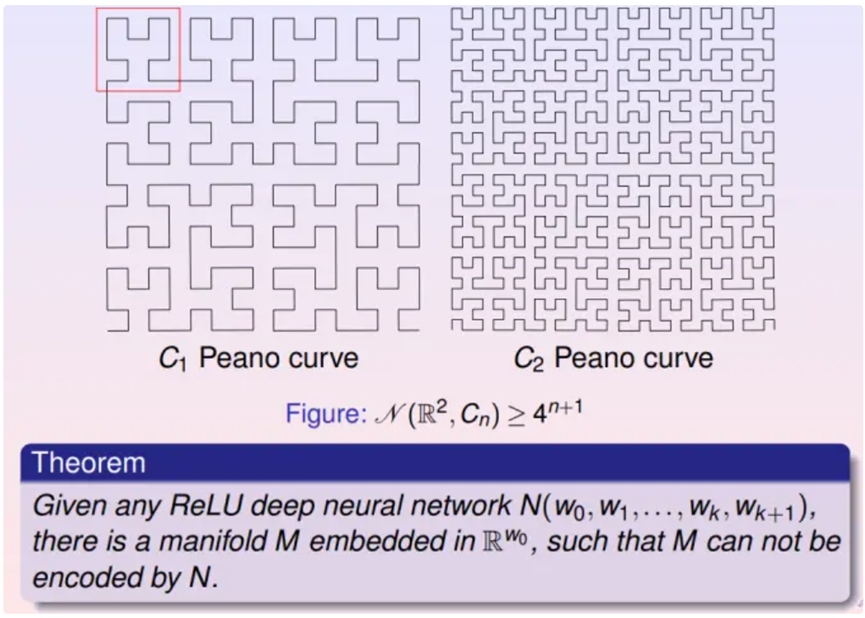
如上图,可以递归定义的Peano曲线,每递归一层,其空间复杂度就会乘以4。通过Peano曲线,可以构造具有任意复杂度的流形。可以用这种流形来检测当前深度神经网络的学习能力。
Probability Measure Learning
(概率测度学习)
Generative Model (生成模型)

用深度神经网络的万有逼近能力来数据流形的拓扑结构,接下来学习概率分布,从而把白噪声转换成数据的概率分布。
GAN model (对抗生成模型)
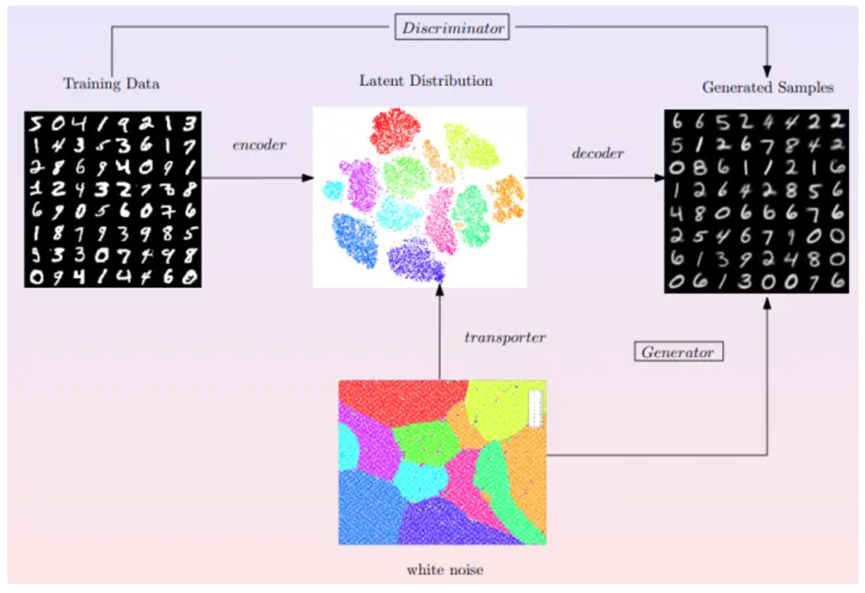
GAN模型通过编码映射将数据流形打到特征空间,并得到隐空间的数据分布;然后在特征空间中生成白噪声,将白噪声变换到隐空间中的采样点;再通过解码将隐空间的采样点映射回到数据流形,得到生成样本。这个过程相当于一个生成器,所有生成图像在数据流形上得到了一个概率分布,即生成分布。判别器计算真实分布与生成分布之间的距离,从而区分这两种分布。
由此GAN模型拥有两套网络——生成器与判别器,并得到以下图解。
GAN Overview (GAN模型概览)

生成器Generator生成虚假的数据分布,判别器Discriminator要识别分布是真是假。那么用数学语言就是说,在特征空间有个白噪声分布,生成器将特征空间的白噪声分布变换成数据流形上的生成分布。图中数据流形上的生成分布是绿色曲线,数据流形上的真实分布是虚线。判别器判别两个分布的相异程度,生成器优化生成分布,使之尽量接近真实分布。两者相互竞争,最终系统达到平衡。
Wasserstein GAN Model
(Wasserstein GAN 模型)

如上图所示,生成器将特征空间的白噪声映射到数据流形上的生成分布,判别器计算从生成分布到真实分布的映射,从而判断其距离。在优化过程中的任意一步,这两个映射的复合直接给出了隐空间上白噪声到数据流形上真实分布的映射,即GAN模型的目标映射。这意味着GAN模型中生成器和判别器的竞争应该被合作而取代,从而提高效率。这里的两个映射都是计算两个概率分布之间的变换,因此都需要用到最优传输理论。
Optimal Transport Framework
(最优传输理论框架)
Overview (概览)

最优传输理论框架如图所示:考察一个黎曼流形上所有可能的概率分布,所有可能的概率分布构成一个无穷维的空间,即Wasserstein空间。深度学习的本质是在Wasserstein空间中优化,挑选出最佳的概率分布,使其满足某些观察(例如期望)并且优化某些能量(例如最大熵值)。

最优传输理论为Wasserstein空间定义了黎曼度量,从而定义了平行移动和协变微分,这使得变分优化得以在Wasserstein空间中施行。这也解释了为什么最优传输理论是深度学习的理论基础。

给定两个概率分布,它们之间的最优传输映射由蒙日-安培方程所控制,两个分布之间的测地线有McCann平移给出,Wasserstein空间某点处的切向量是底流形上的梯度场,其梯度场内积的加权积分定义了Wasserstein空间的黎曼度量。
Brenier’s Approach (Brenier的途径)

最优传输映射是在所有供需平衡的映射中是的总传输代价最小者。Brenier定理断言:如果传输代价是由从供给方到需求方的欧氏距离平方来界定,那么这个最优方案就会由一个凸函数的梯度给出,这个函数就被称为Brenier势能函数,且满足知名的Monge-Ampere方程。

那么如何高效而精确地求解蒙日-安培方程呢?
Convex Geometry
(凸几何)
Minkowski problem - General Case
(Minkowski问题)
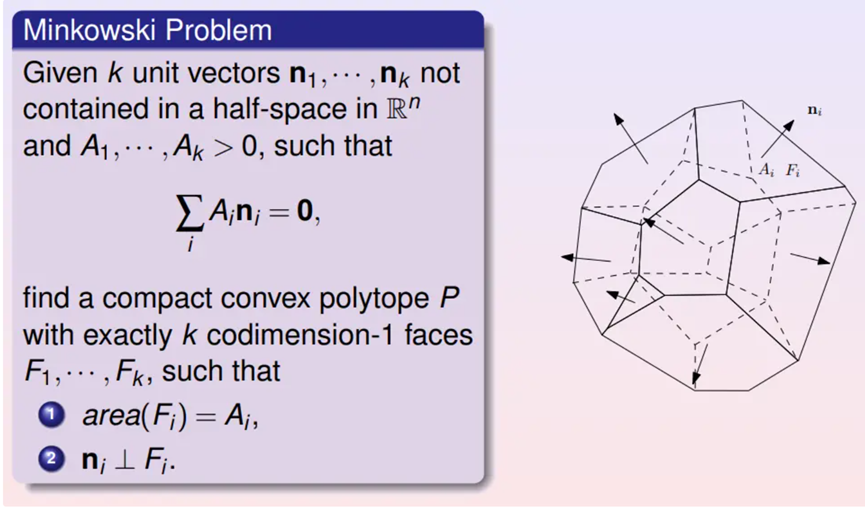
如果在三维空间中给定一个凸多面体,知道每个面的面积和法向量(有向面积),并且有向面积总和为0,可否将这个凸多面体的形状确定下来?这个问题被称为是Minkowski问题。Minkowski证明了解的存在唯一性。
Alexandrov Theorem (Alexandrov 定理)

Alexandrov推广了Minkowski定理:考察开放凸多面体,平面上有一个凸集。凸多面体向平面上平行投影,多面体每个面的投影面积给定,每个面的法向量给定,那么这个凸多面体的形状被唯一确定下来。Alexandrov给出了基于代数拓扑的存在性证明,而需要一个构造性证明。
Variational Proof (变分证明)

2013年,在丘成桐先生的代领下,用几何变分法给出Alexandrov定理的一个构造性证明。Alexandrov定理和Brenier定理是等价的,这给出了最优传输与微分几何的桥梁。
由此,看到深度学习最终可以归结为概率统计,而概率统计中常用的最优传输理论可以用几何方法加以解决。
Computational Algorithm (计算方法)
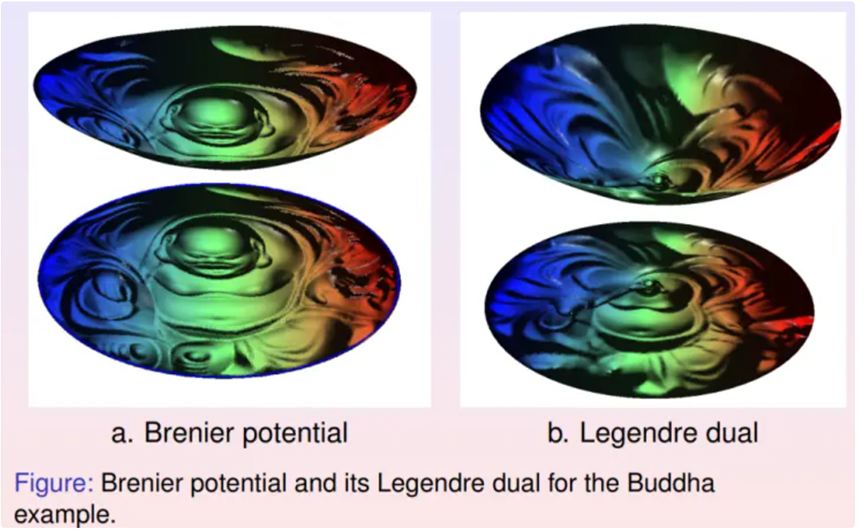
基于定理,可以设计算法求解最优传输映射。黎曼映射将弥勒佛曲面映射到平面单位圆盘上,从而将曲面的面元前推到圆盘上,得到黎曼映射诱导的测度。计算从圆盘上的勒贝格测度到黎曼映射诱导的测度之间的最优传输映射,左帧显示了相应的Brenier势能函数;其逆映射也是最优传输映射,其Brenier势能函数显示在右帧,两个势能函数互为勒让德变换。

由上图,可以看到最优传输变换保持曲面的面积元。
Wasserstein GAN Model (Wasserstein GAN模型)

再来回顾Wasserstein GAN模型,生成器其实可以求解一个最优传输映射,即求解蒙日-安培方程。判别器需要计算两个概率分布之间的Wasserstein距离,这等价于两个概率分布之间最优传输变换对应的总传输代价,因此也归结为求解蒙日-安培方程。
Power Diagram vs Optimal Transport
Map (Power图与最优传输映射)
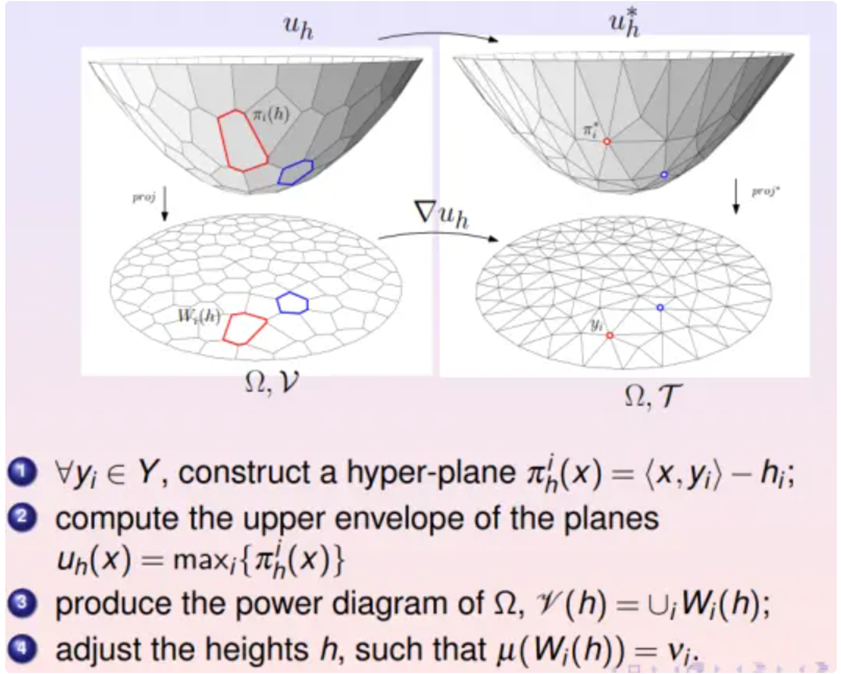
用经典的计算几何算法来求解蒙日-安培方程。在实际深度学习应用中,给定的目标概率分布都是离散的,可以表示成狄拉克概率分布之和。
Semi-discrete Optimal Transportation
(半离散最优传输)
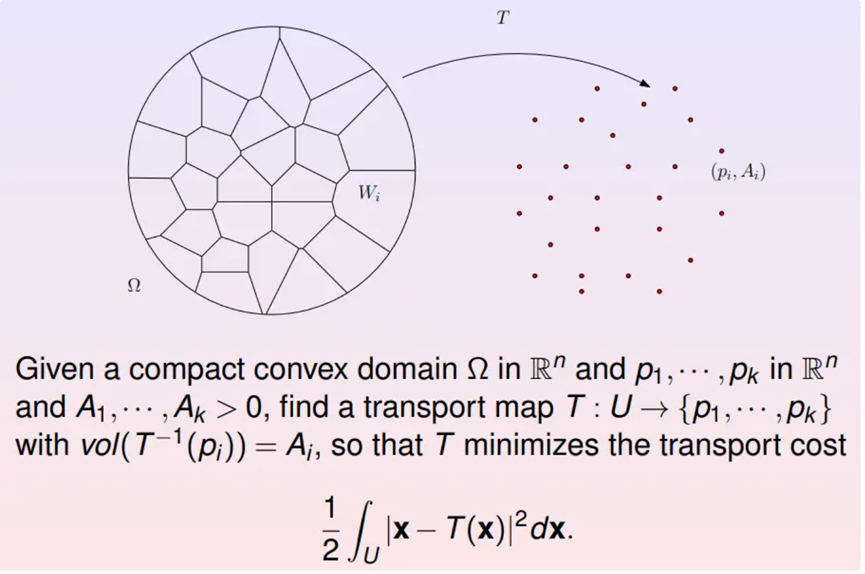
假设源概率分布为单位圆盘内的勒贝格测度,目标概率分布为离散的分布。求解最优传输映射等价于对单位圆盘进行胞腔分解,每个胞腔映射到一个目标采样点,使得胞腔的面积等于这个采样点对应的权重。在所有这样的胞腔分解之寻找总传输代价最少者。根据Brenier定理,这个半离散最优传输映射应该等于某个凸函数的梯度映射。
Power Diagram vs Optimal Transport
Map (Power图和最优传输映射)
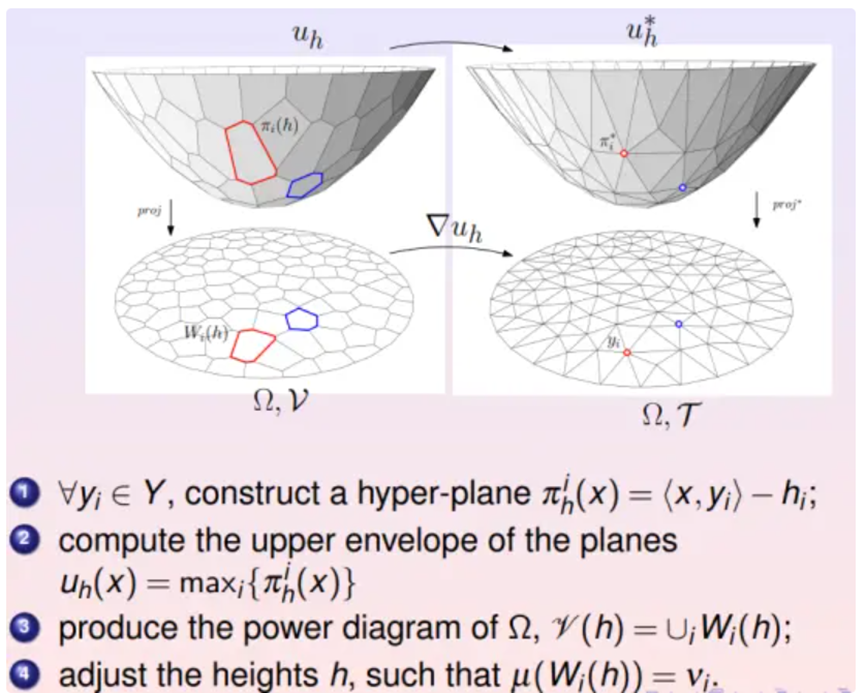
深度学习算法本质上就是学习Brenier势能凸函数。这个势能函数可以表示成很多支撑平面构成的上包络。每个支撑平面将欧氏空间分成上下两半,所有上半空间的交集被称为上包络,其边界就是Brenier势能函数。
Learning Problem (学习问题)

由此看到深度学习算法学习的Brenier势能函数的表达式包含两部分,一部分是所有样本,所有深度学习神经网络记住了所有样本;一部分是每个支撑平面的截距,这是算法提炼出来的内在知识。由此看到所以深度神经网络的确确实记住了所有的训练样本,而且学会了一些新的知识。
Complexity of Geometric Optimal Transport
(几何最优传输的复杂度)
那么深度学习的效果如何呢?目前的算法具有不可避免的内在缺陷,体现为所谓的模式坍塌Mode Collapse现象。
Mode Collapse (模式坍塌)
(1)GAN训练非常困难,对于超参数非常敏感;
(2)GANs 具有模式坍塌现象,生成的分布无法覆盖所有模式;
(3)GANs 会产生失真的样本;
例如用传统的GAN生成了很多人脸图像,但是很多图像看上去根本不像人脸,这种情况就被称为模式坍塌。

Experiments – mnist (Mnist实验结果)

用同样的传统算法生成了许多手写体数字图像,它会生成很多乱七八糟的乱码。模式坍塌是目前深度学习领域最大的问题之一。这个问题是由什么引起的呢?下面用最优传输理论加以解释。
Experiments - Mode Collapse (实验-模式坍塌)
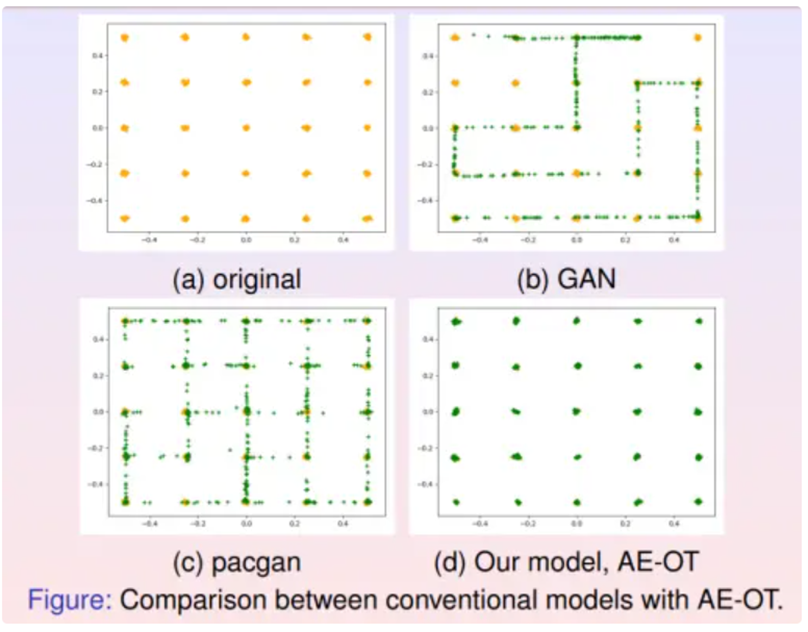
如(a)帧所示,设计了平面上的一个概率分布,分布的支撑集显示为橘黄色的点,每一个点代表一个模式(mode)。GAN模型生成的样本用绿色的点来表示。在(b)帧中,GAN模型生成的绿色样本覆盖了一些橘黄色的点,但是依然有一些橘黄色的点没有被覆盖,这就是模式坍塌现象。在(c)帧中,所有橘黄色的点都被pacgan生成的绿色样本覆盖,即pacgan没有出现模式坍塌,但是它也生成了很多绿色样本介于橘黄色的点之间,这就是模式混淆现象。
模式坍塌现象的本质原因来自于最优传输映射的正则性理论。在经典的蒙日-安培方程理论中,人们研究最优传输映射大多是比较规则的情形,假设密度函数上下有界,支集是边界光滑的凸集,由此能够证明解的光滑性。但是如果目标区域非凸,则解可能非光滑,存在奇异集合。例如上届菲尔兹奖得主Figalli给出下面的例子:

在平面上有两个概率分布,左侧是单位圆盘上的均匀分布,右侧是海马形状区域中的均匀分布。计算最优传输映射,在圆盘内部有黑色的曲线,映射在这些曲线处间断。这意味着如果目标区域是非凸的,最优传输映射就有可能是非连续的。
在深度学习中,一切变换都用深度神经网络来表示。但是深度神经网络只能表达连续变换,而最优传输变换是非连续的。其非连续性使得深度神经网络无法学会,只会收敛到错误结果上。那么又该如何避免模式坍塌的问题呢?
Optimal Transportation Map
(最优传输映射)
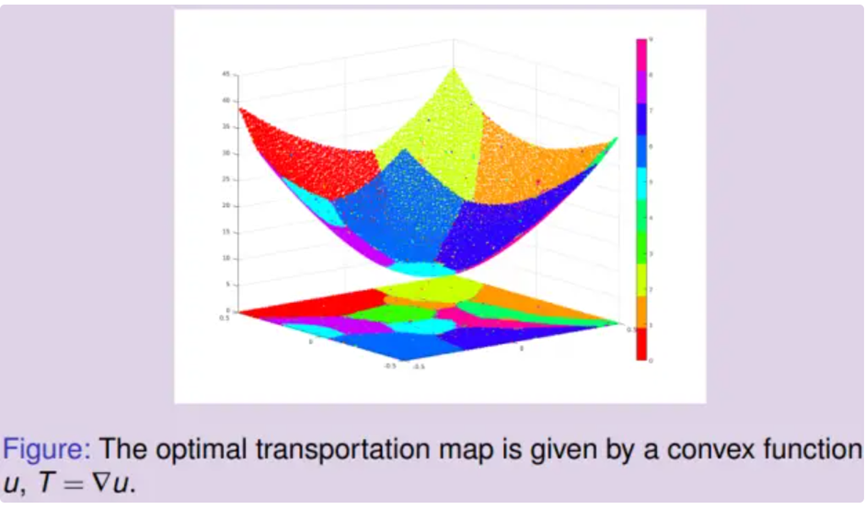
针对上述问题提出了解决方案。最优传输映射由Brenier势能函数的梯度给出来,它可能是非连续的。但是Brenier势能函数本身确是整体连续的,但可能是非光滑的。因此可以用深度神经网络表达Brenier势能函数,而非最优传输映射。
Singularity Set Detection (奇异集合检测)
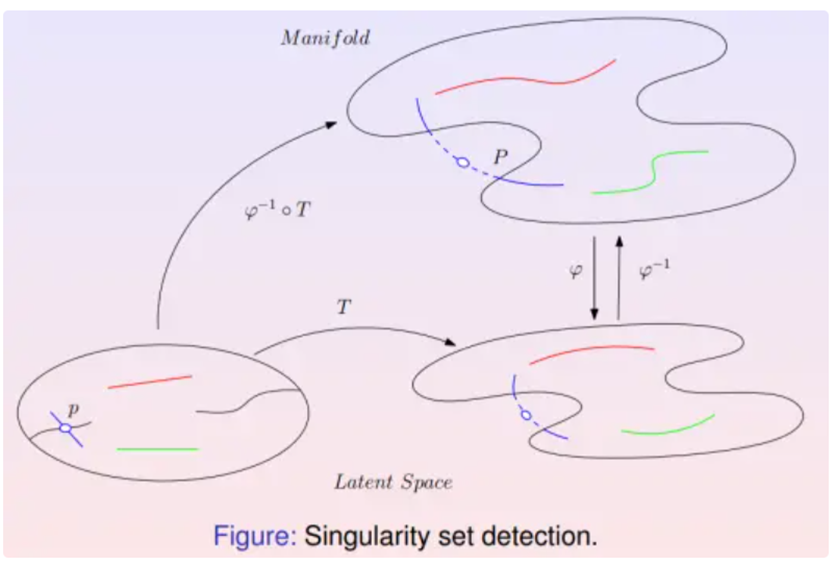
设计了一个物理实验来验证想法。如图所示,用人脸图像集训练了一个数据流形,并用自动编码器将其映射到隐空间,降维到100维;然后在隐空间中求出白噪声分布到数据分布之间的最优传输映射。在白噪声支集内画了很多直线段,每条线段映成了特征空间上的一条曲线,后又映成数据流形上的一条曲线。流形上的每个点代表一个图像,一条连续曲线代表了人脸图像的连续变化过程。
如果最优传输变换存在奇异集合,那么某条线段可能会和奇异集合产生交点,这些交点被映射成人脸图像流形的边界。会在边界处看到这样的人脸图像,它们即在生理学上是合理的,但是在现实中碰到的概率为零。

如图右帧所示,从左上角棕发黑睛的男孩人脸开始,到右下角金发碧眼的女性结束,中间有一些图像是一只眼睛为黑色而另外一只眼睛为蓝色。这些人脸图像生理学上是合理的,但在现实生活中遇到的概率为零。
发现这个过程穿越了流形的边界。其中生成的一些图片虽然合理,但是现实中碰到的概率为0。这也在一定程度上说明想象是合理的,人脸流形存在边界,产生的映射是连续的。
如何来避免模式坍塌呢?建立了如下模型。
Auntoencoder-OMT (自编码器-最优传输模型)

知道深度学习主要有两个核心任务:一是学习流形的拓扑结构,一是学习概率分布。将这两个任务解耦,流形拓扑结构用自动编码器来实现,概率分布通过最优传输理论利用几何方法来学习。模式坍塌主要由第二部分引起,用几何方法可以避免模式坍塌。从实验结果与传统方法的结果对比来看,这种方法完美避免了模式坍塌,提高了系统的可解释性。
Conclusion (结论)
通过几何和拓扑的观点,为深度学习建立了一个可解释的框架。
(1)每个自然(视觉)概念都对应物理世界中的一个数据集,其数学描述是嵌入在高维背景空间中的低维数据流形上的某种特定概率分布。
(2)深度学习的核心任务被解耦成两部分,一是学习数据流形的拓扑结构,一是学习流形上的概率分布
(3)数据流形拓扑结构的学习主要是用万有逼近定理,将流形映射到特征空间(隐空间);概率分布的学习实际是应用最优传输理论。最优传输理论为Wasserstein空间赋予了黎曼度量和协变微分,为在所有概率测度构成的空间中优化提供了理论框架。
(4)概率论中的Brenier理论和微分几何中的Minkowski-Alexandroff理论等价,从而可以从几何角度来解释概率统计,用几何变分法来求解最优传输映射。
(5)根据Brenier定理,看到GAN模型中的生成器和判别器应该合作而不是竞争,从而提高计算效率。
(6)根据Monge-Ampere方程的正则性理论,可以解释深度学习最核心的问题——模式坍塌。
(7)提出了一种新的几何框架,来设计新的深度学习模型以避免模式坍塌。
参考文献链接
https://ishare.ifeng.com/c/s/v002JgwF4NYcbmQ82S4-_eS-_3--f5R3EL7B4JxV5Rtmq7LCNA__