目录
- 0、综述:
- SGD
- 1、mini-batch
- 2、指数平均加权
- 3、理解指数加权平均
- 4、指数加权平局的修正
- 5、动量梯度下降法
- 6、RMSprop
- 7、Adam优化算法
- 8、衰减率
- 9、局部最优
0、综述:
在VSLAM后端中有各种梯度下降优化算法,例如:最速下降法、牛顿法、高斯-牛顿法、LM法、Dog-Leg法等。梯度下降优化其实就做了两件事:一是找一个好的下降起点;二是每次迭代,找一个好的增量。第一点参考以前博客:xxxxx,现在搞DL,重点研究第二点。
吴恩达课程:https://www.bilibili.com/video/BV1i741147Q5?p=22
本博客重点参考吴恩达课程,并有个人理解。
Momentum动量:利用衰减指数,对历史梯度进行加权平均(距离当前点越近,权系数越大),得到新的模型参数(w、b),好处是新的模型参数更加平滑,不会有剧烈震荡,易于收敛,比标准梯度下降收敛更快。
RMSprop:通过简单在增量分母增加一个根号梯度值,使得原本下降得慢的优化变量下降得快,原本下降得快的变慢,有效消除震动。
(注:这句话中“原本下降的慢”的原因是:其增量,也就是Δx = -dy/dx(即:负梯度),本身比较小,也可以理解为在x处变化率小,Δx小,梯度下降自然就是慢!)
Adam:Momentum + RMSprop,通用性公认最强。
超参数:学习率、衰减率、动量,如何管理、搜索、调整
总结:
1、mini-batch
假定你有5万个样本,每个mini-batch以1000个样本为一个子集,这样就有50个mini-batch。那么,每个epoch并行处理50个mini-batch,以便遍历完整个训练集。
算法小结:例如这里要跑50个epoch,在每个epoch中:
1、如上述所述,将数据分为50组,作并行处理,即将50组数据同时输入网络;
2、得到50个loss,求和并除50得到新的loss_;
(利用loss求解梯度:reference: https://www.cnblogs.com/winslam/p/12889014.html)
3、接着利用loss_进行反向传播,更新权重,当前epoch结束。
优点:在一个opeoch中,这样处理比遍历5万次要快,因为中间有并行处理
2、指数平均加权
全称:指数加权移动平均值,其实就是指数-加权-移动-平均值。好处是:让数据更加平滑,但是可能失真???
下图左边是地区半年来,每天的气温数据,右边是温度变化曲线
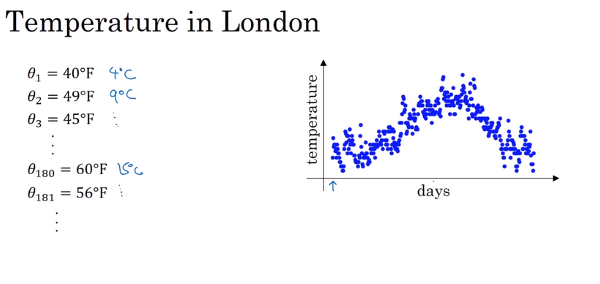
作如下处理,下面v(t)(t = 1 2 3 ...181)表示重新计算后的温度,其实计算公式是:当天温度 = 前一天温度 * 0.9 + 当天温度 * 0.1,一个加权线性变换而已:
(下面公式抽象为:v(t)= β * v(t-1) + (1 - β) * θ(t),下面的计算中,β = 0.9 )
v(0) = 0
v(1) = 0.9 * v(0) + 0.1 * θ1
v(2) = 0.9 * v(1) + 0.1 * θ2
v(3) = 0.9 * v(2) + 0.1 * θ3
...
你看上边所有的方程,等号右边第一项如果看作为0,
那么当β = 0.9 时, 1-β = 0.1,此时,v(t)可以看作:过去10天的平均值,如下图红色曲线
如果当β = 0.98 时, 1-β = 0.02,此时,v(t)可以看作:过去50天的平均值,如下图绿色曲线
,可以看到β值调高以后(β = 0.98),好处是:数据变得平滑,坏处是:数据整体向右边移动(拿历史50个数进行均值滤波),那么将β调得非常低,又会怎样?
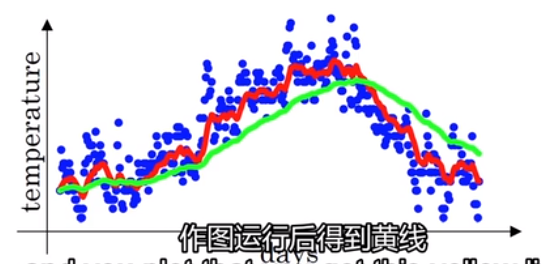
当β = 0.5的时候,v(t)可以看作过去两天平局温度,如下图, 和原始数据一样比较震荡。
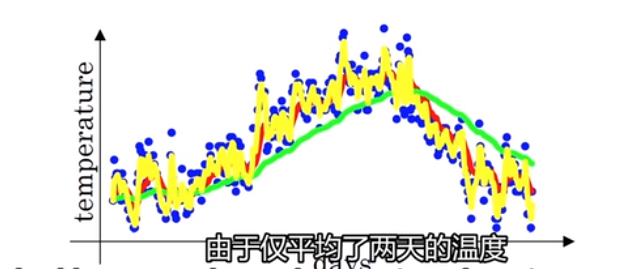
3、理解指数加权平均
还是上面的温度,这里写出1-100天的气温计算公式(下面“()”表示下表):
v(t) = β * v(t-1) + (1-β)*θ(t)
v(100) = 0.9 * v(99) + 0.1 * θ(100) ..........................................(1)
v(99 ) = 0.9 * v(98) + 0.1 * θ(99) ..........................................(2)
v(98) = 0.9 * v(97) + 0.1 * θ(98) ..........................................(3)
...
这里将上面第一个方程重写:
v(100) = 0.1 * θ(100) + 0.9 * v(99) # 代入上述方程(2)得到下一行
= 0.1 * θ(100) + 0.9 * [0.1 * θ(99) + 0.9 * v(98)] # 代入上述方程(3)得到下一行
= 0.1 * θ(100) + 0.9 * [0.1 * θ(99) + 0.9 * [0.1 * θ(98) + 0.9 * v(97)]] # 下一行直接展开看看
= 0.1 * θ(100) + 0.9 * 0.1 * θ(99) + 0.9^2 * 0.1 * θ(98) + 0.9^3 * v(97) # 后续的v(96)、v(95)......不再写开,假定咱们写开了吧,懒得写而已
由上述式子,我们知道,第100天的气温v(100)和历史100天都有关,实际上就是历史一百天的加权平均值,其中加权系数记向量a:
a = [0.1, 0.9 * 0.1, 0.9^2 * 0.1......];
构建指数衰减函数(decay-function,例如:β 取 0.9):
f(n) = (1-β) * (β)^n = 0.1 * 0.9^n (n = 0 1 2 3 ......)(上述向量a符合该函数)
f(n)曲线如图:

上面的温度数据:

上述v(100)的最终推导结果,其实就等于衰减函数中的每一项与温度原始数据相乘,求和。v(100)中所有项系数加起来等于1 或者接近1,同时也可以看到,距离第100天越近,权系数越大,距离越远,权系数越小。
4、指数加权平局的修正
上一节已经学习了如何计算指数加权平均,这一节重点介绍“偏差修正”,本质:重点修正前期偏差,使得数据前期指数加权平均计算更加准确,尽管这一节的技术并不怎么实用。
在上述博客中,我们知道β = 0.98对应下面绿色曲线。

实际上,下图紫色曲线才是β = 0.98 对应的曲线。可以看到,紫色曲线起点相对绿色比较低,到后面才“追赶上”。

为什么初始数据比较低呢?我们将上述加权平均温度公式搬下来(这里β = 0.98),如下:
v0 = 0
v(1) = 0.98 * v(0) + 0.02 * θ1 = 0.02 * θ1
v(2) = 0.98 * v(1) + 0.02 * θ2 = 0.98 * 0.02 * θ1 + 0.02 * θ2
v(3) = 0.98 * v(2) + 0.02 * θ3 = ...
...
可以看到,前几项权重系数非常小,所以β = 0.98的时候,得到温度结果很落后。怎么修正前期误差呢?
将v(t, t = 0 1 2 3 ...100)除以一个(1 - β^t),即:
令v(t) = v(t) / (1 - β^t)
可以验证下:
v0) = 0
v(1) = (0.98 * v(0) + 0.02 * θ1 )/ (1 - β^t)= 0.02 * θ1 / (1 - 0.98^1) = θ1
v(2)= (0.98 * v(1) + 0.02 * θ2)/ (1 - β^t) = (0.98 * 0.02 * θ1 + 0.02 * θ2) / (1 - β^t) = ((0.98 * 0.02 )* θ1 + 0.02 * θ2)/ 0.0396
v(3) = (0.98 * v(2) + 0.02 * θ3)/ (1 - β^t) = ...
可以看到v(1)修正前为:v(1) = 0.02 * θ(1),修正后有:v(1) = θ(1),显然修正后,有效避免了β = 0.98时,前期数据过于落后的问题。
对于上述修正公式,我们注意到分母,当β = 0.98时,当t越来越大,1/(1 - β^t) 越接近于1,修正效果越小,这是我们希望看到的,因为数据也仅仅是前期的落后(就是t比较小的时候),当t比较小的时候才有修正作用。
如下图,训练过程中,当你在热身训练时(warming-up)
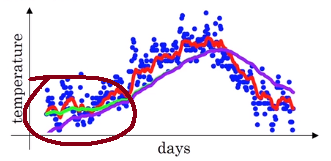
小结:在实际训练中,其实对于采用指数加权平均处理数据时,上述修正方法其实用得不多,不在乎执行偏差修正,因为大部分宁愿熬过初始时期,尽管得到参数模型的loss较大,但是后续接着给网络喂中间、后面的数据,也能得到一个好的结果。
5、动量梯度下降法
如下图,优化的全局最优值是如图红点,常规梯度下降的路径如图蓝色路径,可以看到迭代次数较多,尤其是接近收敛点附近。这里,如果所示,优化的变量应该有两个,在纵轴方向,我们希望增量变化慢一点,而在横轴方向希望快一点,所以本小节介绍
动量梯度下降法来解决这一问题。

Momentum动量算法如下(这里有两个超参数:α、β):
对于某一次迭代:
在当前mini-batch中,计算增量v(dw)、v(db),(dw、db表示历史增量),计算公式如下:
v(dw) = β * v(dw) + (1 - β) * dw
v(db) = β * v(db) + (1 - β) * db
更新网络参数(α是学习率数):
w = w - α * v(dw)
b = b - α * v(db)
如下图,红色路径是采用了上述动量算法计算增量的结果,显然红色路径相对蓝色路径,更加平稳,不那么震荡,更快收敛于最优点,一般地,动量超参数β设置为0.9左右比较好。

从物理学角度看待上述动量方程:
v(dw) = β * v(dw) + (1 - β) * v(dw)
v(db) = β * v(db) + (1 - β) * v(db)
将蓝色视为速度,红色视为加速度,上图梯度下降过程视为:一个小球从山顶滚下来,在山顶附近:加速度大,速度小;在山脚附近,加速度很小,速度很大,但是平稳,接近匀速。
6、RMSprop(root mean square prop)
上一节动量可以加速收敛,这一节RMSprop也有加速收敛效果。还是上面那张图,

RMSprop算法流程如下:
对于某一次迭代:
在当前mini-batch中,计算增量新的v(dw)、v(db),计算公式如下(其中,符号⊙表示两个向量对应元素相乘):
v(dw) = β * v(dw) + (1 - β) * dw⊙dw...............................(1)
v(db) = β * v(db) + (1 - β) * db⊙db ...............................(2)
更新网络参数(α是学习率系数):
(注:在公式(3)、(4)中,为了避免分母为0,在分母可以添加一个较小的常数,例如:1e-8,我这里省略不写了。)
w = w - α * dw / sqrt(v(dw))...............................(3)
b = b - α * db / sqrt(v(db))...............................(4)
分析:如上图,咱们希望在横轴w方向上步伐(增量)走得快一点,b轴方向走得慢一点,这样能有效避免震荡。如上公式(1)、(2)计算出v(dw)、v(db),与第5节动量中算法不一样,第五节中v(dw)、v(db)直接表示的是增量,在这一节中,用作公式(3)、(4)的分母,上述公式中,dw / sqrt(v(dw)) db / sqrt(v(db)) 才是增量,可以从上图看到,w轴方向的变化率相对b轴要小,即:dw相对小,db相对大,那么v(dw)小,v(db)大,则导致增量(步伐)dw / sqrt(v(dw))大、db / sqrt(v(db))小,最终达到咱们的需求,即:在w轴方向大步伐走,在b轴上小步伐走。下面捋一遍:
如上图,
- dw小 -> 如公式(1),v(dw) 小 -> 增量dw / sqrt(v(dw))大 -> w 变化大
- db大 -> 如公式(2),v(db) 大 -> 增量db / sqrt(v(db))小 -> b 变化小
(dw在这里是差分,表示导数、变化率)
小结:RMSprop和Momentum都可以消除下降过程中的抖动,RMSprop算法居然不是议论文的形式发布,而是公开课。下一节讲述如何将二者进行结合。
7、Adam(adaptive Moment Estimation)优化算法
实践表明,RMSprop、Adam算法相对于Momentum算法更加通用,适用于各种神经网络,Adam = RMSprop + Momentum。
Adam算法流程如下:
对于某一次迭代:
在当前mini-batch中,计算增量新的v_m(dw)、v_m(db)和v_r(dw)、v_r(db)和v_m_corr(dw)、v_m_corr(db)、v_r_corr(dw)、v_r_corr(db)
(下表m、r、corr分别表示采用Momentum、RMSprop计算出的数值,m_corr、r_corr表示对应矫正后的值),计算公式如下(其中,符号⊙表示两个向量对应元素相乘):
v_m(dw) = β1 * v_m(dw) + (1 - β1) * dw ...............................(1) Momentum
v_m(db) = β1 * v_m(db) + (1 - β1) * db ...............................(2) Momentum
v_r(dw) = β2 * v_r(dw) + (1 - β2) * dw⊙dw...............................(3) RMSprop
v_r(db) = β2 * v_r(db) + (1 - β2)* db⊙db ...............................(4) RMSprop
对上述方程左边算出的四个值进行矫正(t:第几个mini_batch):
v_m_corr(dw) = v_m(dw) / (1 - β^t)...............................(5)
v_m_corr(db) = v_m(db) / (1 - β^t)...............................(6)
v_r_corr(dw) = v_r(dw) / (1 - β^t) ...............................(7)
v_r_corr(db) = v_r(db) / (1 - β^t) ...............................(8)
更新网络参数(α是学习率系数):
(注:e是一个较小的常数,例如:1e-8)
w = w - α * v_m_corr(dw) / sqrt(v(v_r_corr(dw) + e))...............................(9)
b = b - α * v_m_corr(db) / sqrt(v_r_corr(db) + e)...............................(10)
上述Adam算法中有很多超参数,
学习率α:这个需要调整。
β1:经验值认0.9 (用于计算Momentum中的dw 加权平均值)
β2:经验值0.9999(用于计算RMSprop中的dw⊙dw 加权平均值)
e:1e-8
8、衰减率
传统参数更新方程为:
x = x - α * Δx
上式中,α为学习率,如果设置为定值,那么梯度下降过程中,下降的步伐基本上由Δx决定,在一些优化任务中,如果你运气不好,会导致优化路径走出锯齿状,难以收敛。
现在假定要跑100个epoch,每个epoch中迭代10,每次迭代batch_size设置为8,我们给出下面方程:
x = x - 1 / (1 + decay_rate * epoch_num) * α * Δx
红色分数相当于给衰减率a增加一个约束,decay_rate:衰减率,epoch_num:当前是第几个epoch,
训练之前,衰减率、学习率时都要调一下的。上式中,学习率的约束项(红色部分),还有其他写法,如下式子:
0.95^epoch_num
9、局部最优

1、如上图,就是一个小锯齿,在前面变化率较小的时候,走了很多步,收敛很慢,但是只要迭代次数足够多,也能够渡过该阶段。
2、针对上述收敛很慢等问题,我们有Momentum、RMSprop、Adam这样的算法,使得下降过程能够快速收敛,尽早地走出平稳阶段。