1.标量
仅包含一个数值被称为标量。

2.向量
向量被视为标量值组成的列表,这些标量被称为向量的元素,在数学上,具有一个轴的张量表示向量。一般来说,张量可以具有任意长度,这取决于机器的内存。

3.长度、维度、形状
向量的长度通常称为向量的维度,我们可以用Python内置函数len访问张量长度。

当用张量(只有一个轴)表示一个向量时,也可以用.shape访问向量的长度,列出张量沿每个轴的长度,对于只有一个轴的张量,形状只有一个元素。

在此区别,向量或轴的维度被用来表示向量和轴的长度,即向量和轴的元素数量。而张量的维度用来表示张量具有的轴数。在这个意义上,张量的某个轴的维数就是这个轴的长度。
4.矩阵
类比向量将标量从零阶推广到一维,矩阵又将向量从一维推广到二维。
\[A = \left[ \begin{matrix} a_{11} & a_{12} & a_{13} & \cdots & a_{1n} \\ a_{21} & a_{22} & a_{13} & \cdots &a_{2n}\\ \vdots & \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & a_{m3} & \cdots &a_{mn} \end{matrix} \right]
\]
A的形状时(m,n),当行列数量相等时,称为方阵。
我们可以通过行索引i,列索引j访问矩阵元素aij,例如[Aij]。
当我们交换矩阵行列时,结果称为转置。用B=AT表示。有aij=bji,因此形状是(n,m)的矩阵。
\[B = \left[ \begin{matrix} a_{11} & a_{12} & a_{31} & \cdots & a_{m1} \\ a_{12} & a_{22} & a_{32} & \cdots &a_{m2}\\ \vdots & \vdots & \vdots & \ddots & \vdots \\ a_{1n} & a_{2n} & a_{3n} & \cdots &a_{mn} \end{matrix} \right]
\]

方阵的一种特殊类型,对称矩阵,即B=BT。
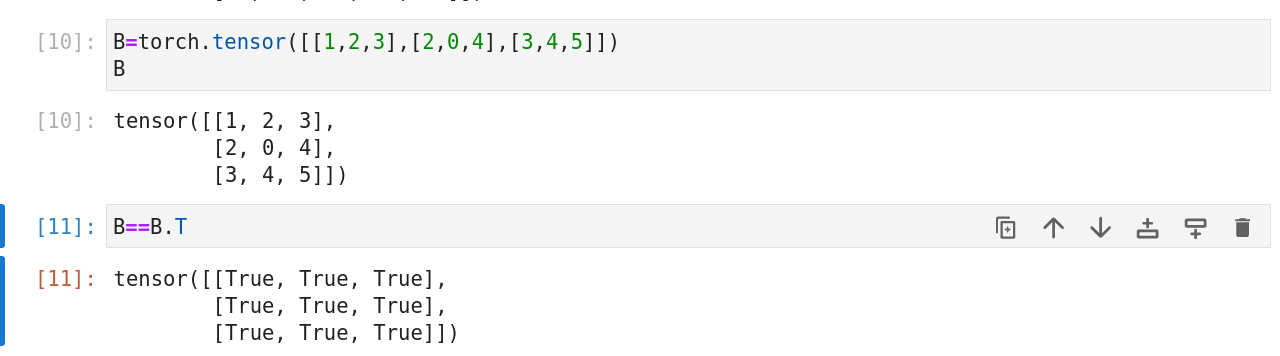
尽管,单个向量的默认方向是列向量,但在表示表格数据集的矩阵中,将每个数据样本作为矩阵中的行向量更为常见。
5.张量
张量是描述具有任意数据轴的n维数组的通用方法。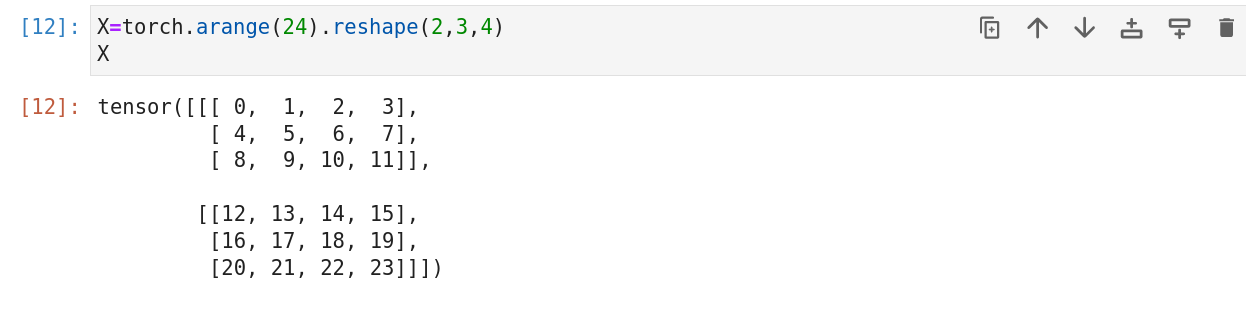
6.张量算法的基本性质
给定具有相同形状的任意两个张量,任何按元素二元运算的结果都将是相同形状的张量。例如将两个相同形状的矩阵相加,会在这两个矩阵上执行元素加法。
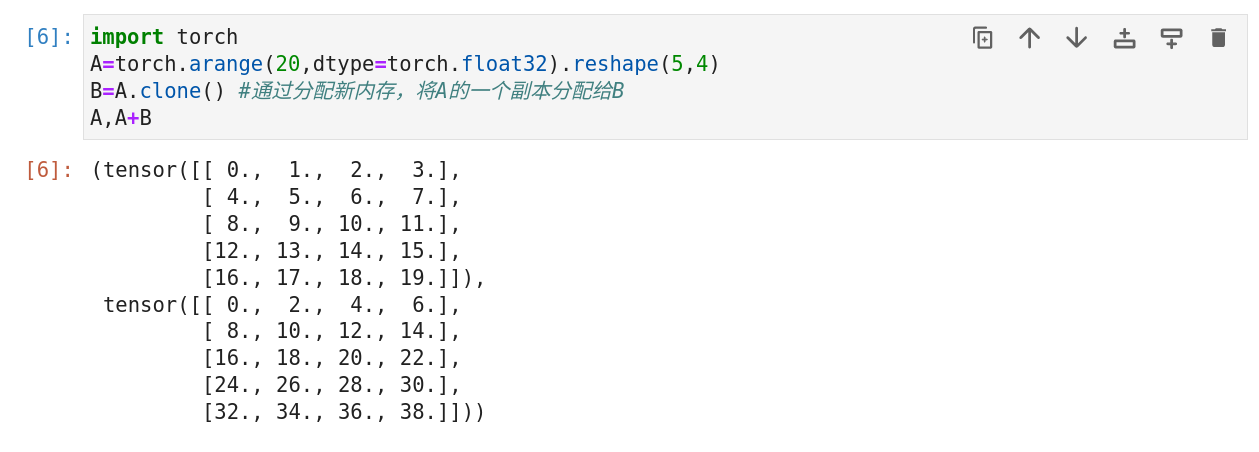
具体而言,两个矩阵的按元素乘法称为哈达玛积,对于矩阵B符合(m,n),第i行第j列元素的元素是bij,矩阵A和矩阵B的哈达玛积为
\[A\circ B =\left[ \begin{matrix} a_{11}b_{11} & a_{12}b_{12} & a_{13}b_{13} & \cdots & a_{1n}b_{1n} \\ a_{21}b_{21} & a_{22}b_{22} & a_{13}b_{13} & \cdots &a_{2n}b_{2n}\\ \vdots & \vdots & \vdots & \ddots & \vdots \\ a_{m1}b_{m1} & a_{m2}b_{m2} & a_{m3}b_{m3} & \cdots &a_{mn}b_{mn} \end{matrix} \right]
\]

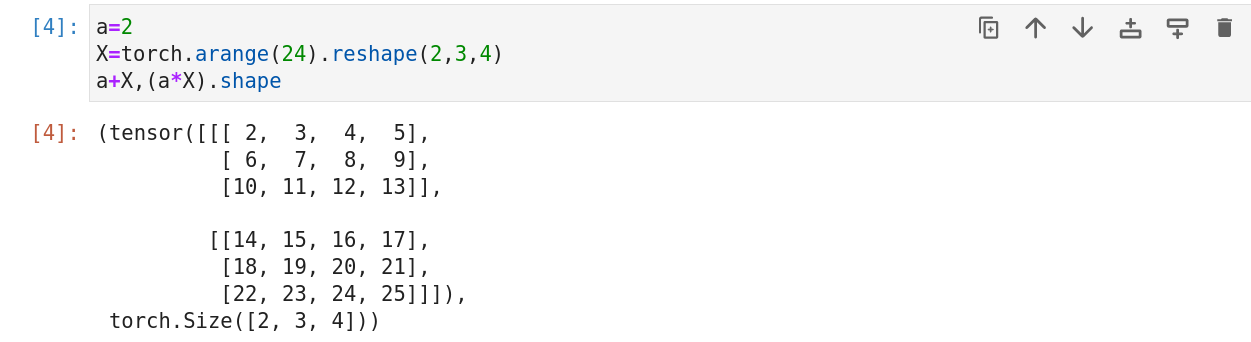
将张量加上或乘以一个标量不会改变张量的形状,其中张量的每个元素都将与标量相乘或相加。
7.降维
我们可以对任意张量进行一个有用的操作是计算其元素的和。为表示长度为d的向量中元素的总和,可以记为
\[\sum_{i=0}^dx_i
\]

同样,我们可以表示任意张量的元素和,例如矩阵A的元素和可以记为
\[\sum_{i=1}^m\sum_{j=1}^na_{ij}
\]

默认情况下,调用求和函数会对所有列的元素求和来降低张量维度,使它变成一个标量。我们还可以指定张量沿哪一个轴来进行降维。以矩阵为例,为了通过对所有行元素求和来降维,在调用函数市可以指定axis=0。对输入矩阵沿轴0进行降维以生成输出向量,因此输入轴0的维数将会在输出形状中消失。

指定axis=1即为对所有列元素进行求和降维。
沿着行和列求和,等价于对矩阵所有元素进行求和。

一个与求和相关的量是平均值(mean或average)。我们通过将总和除以元素总数来计算平均值。在代码中,我们可以调用函数来计算任意形状张量的平均值。
同样,计算平均值的函数也可以沿指定轴降低张量维度。

8.非降维求和
有时,调用函数来计算总和或平均值时保持轴数不变很有用。
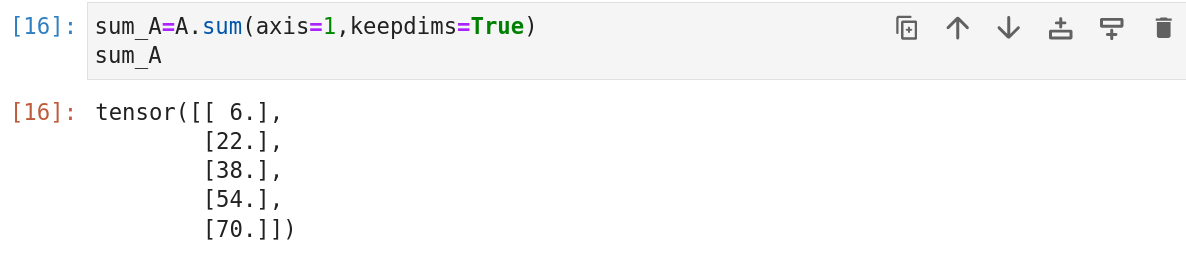
例如,由于sum_A在对每行进行求和后仍然保持两个轴,我们可以通过广播将A除以sum_A。

如果我们沿某个轴计算A的元素的累积总和,如axis=0,可以调用cumsum函数。此函数不会沿任何轴降低输入张量的维度。

9.点积
给定两个向量,它们的点积是相同位置按元素乘积的和:
\[x^Ty=\sum_{i=0}^dx_iy_i
\]

我们也可以通过执行按元素乘法,然后求和来表示两个向量的点积:

10.矩阵-向量积
我们将前面的矩阵A用它的行向量来表示:
\[A= \left[ \begin{matrix} a_1^T \\ a_2^T \\ \vdots \\ a_m^T \end{matrix} \right]
\]
其中,每个aiT表示矩阵第i行,矩阵向量积是一个长度为m的列向量,其第i个元素是点积aiTx:
\[Ax=\left[ \begin{matrix} a_1^T \\ a_2^T \\ \vdots \\ a_m^T \end{matrix} \right]x=\left[ \begin{matrix} a_1^Tx \\ a_2^Tx \\ \vdots \\ a_m^Tx \end{matrix} \right]
\]
在代码中,我们使用张量表示矩阵-向量积。我们使用mv函数。注意A的列维数必须与x的维数相同。

11.矩阵-矩阵乘法
假设有两个矩阵A(n,k),B(k,m):
\[A = \left[ \begin{matrix} a_{11} & a_{12} & a_{13} & \cdots & a_{1k} \\ a_{21} & a_{22} & a_{13} & \cdots &a_{2k}\\ \vdots & \vdots & \vdots & \ddots & \vdots \\ a_{n1} & a_{n2} & a_{n3} & \cdots &a_{nk} \end{matrix} \right],
B = \left[ \begin{matrix} b_{11} & b_{12} & b_{13} & \cdots & b_{1m} \\ a_{21} & b_{22} & b_{13} & \cdots &b_{2m}\\ \vdots & \vdots & \vdots & \ddots & \vdots \\ b_{k1} & b_{k2} & b_{k3} & \cdots &b_{km} \end{matrix} \right]
\]
用行向量aiT表示矩阵A的第i行,并用bj表示矩阵B的第二列。要生成矩阵积C=AB,最简单的方法是考虑A的行向量和B的列向量:
\[A= \left[ \begin{matrix} a_1^T \\ a_2^T \\ \vdots \\ a_m^T \end{matrix} \right],
B= \left[ \begin{matrix} b_1^T & b_2^T & \dots & b_m^T \end{matrix} \right]
\]
当我们简单地将每个元素cij计算为点积aiTbj:
\[C=AB=\left[ \begin{matrix} a_1^T \\ a_2^T \\ \vdots \\ a_m^T \end{matrix} \right]\left[ \begin{matrix} b_1^T & b_2^T & \dots & b_m^T \end{matrix} \right]=\left[ \begin{matrix} a_{1}^Tb_1 & a_{2}^Tb_2 & \cdots & a_{1}^Tb_m \\ a_{2}^Tb_1 & a_{2}^Tb_2 & \cdots &a_{2}^Tb_m\\ \vdots & \vdots & \ddots & \vdots \\ a_{n}^Tb_1 & a_{n}^Tb_2 & \cdots &a_{n}^Tb_m \end{matrix} \right]
\]
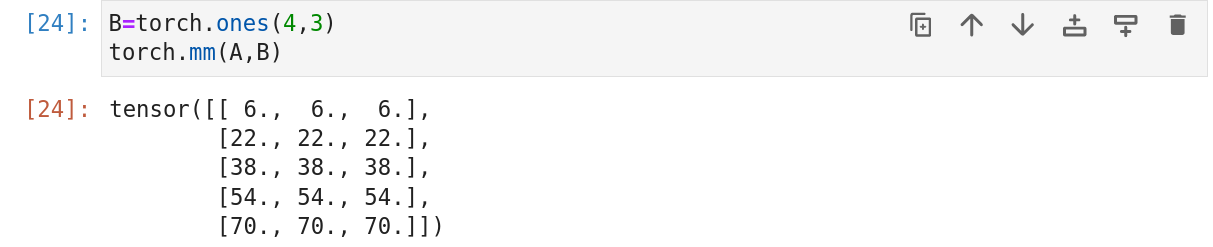
矩阵-矩阵乘法可以简单称为矩阵乘法,不要与哈达玛积混淆。
12.范数
非正式地说,向量的范数表示一个向量的大小,这里的大小概念不涉及维度,而是分量的大小。
在线性代数中,向量范数是将向量映射到标量的函数f,给定任意向量x,向量范数具有一些性质。
第一个性质是:如果我们按照常数因子a缩放向量的所有元素,其范数也会按照相同常数因子的绝对值缩放:
\[f(ax)=|a|f(x)
\]
第二个性质是三角不等式:
\[f(x+y)\leqslant f(x)+f(y)
\]
第三个性质简单来说范数必须是非负的:
\[f(x) \geq 0
\]
因为在大多数情况下,任何数最小的大小是0.最后一个性质要求范数最小为0,当且仅当向量全由0组成:
\[\forall i,[x]_i=0\iff f(x)=0
\]
范数可以类比于距离的度量。事实上,欧几里得距离是一个L2范数。假设n维向量x中元素是x1...,xn,其L2范数范数是向量元素平方和的平方根
\[||x||_2= \sqrt{\sum_{i=1}^nx_i^2}
\]
其中,L2范数常常省略下标2,也就是说||x||等同于||x||2,在代码中我们可以按如下方式计算向量的L2范数:

深度学习中常使用L2范数的平方,也会遇到L1范数,它表示为向量元素的绝对值的和:
\[||x||_1=\sum_{i=1}^n|x_i|
\]
与L2范数相比,L1范数收异常值影响较小。为计算L1范数,我们将绝对值函数和按照元素求和组合起来。
L2和L1范数都是更一般的Lp范数特例:
\[||x||_p=(\sum_{i=1}^n|x_i|^p)^{1/p}
\]
类似于L2范数,矩阵(m,n)的弗罗贝尼乌斯范数是矩阵总元素平方和的平方根:
\[||x||_F=\sqrt{\sum_{i=1}^m\sum_{j=1}^nx_{ij}^2}
\]
弗罗贝尼乌斯范数具有向量范数的所有性质,它就像是矩阵形向量的L2范数,调用以下函数将计算矩阵的弗罗贝尼乌斯范数。

在深度学习中,我们经常试图解决优化问题:最大化分配给观测数据的概率;最小化预测函数值与真实观测值之间的距离。用向量表示物品,以便最小化相似项目之间的距离。除了数据目标或许是深度学习算法最重要的组成部分,通常被表达为范数。



























