[KDD 2023] All in One- Multi-Task Prompting for Graph Neural Networks
总结
提出了个多任务prompt学习框架,扩展GNN的泛化能力:
- 统一了NLP和图学习领域的prompt格式,包括prompt token、token structure、inserting pattern
- 构建诱导子图,将点级和边级任务改造为图级任务,统一不同级别的图任务
- 引入元学习技术学习更可靠的多任务prompt,适应多种图任务。
动机
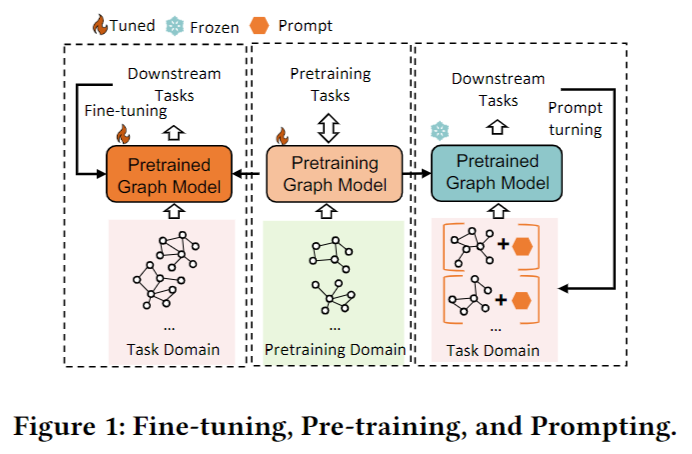
NLP中的prompt learning的思路能够利用预训练语言模型处理经过改编的文本输入,从而将预训练模型泛化到广泛的下游语言任务中。本文希望利用这个思想来实现一个泛化的GNN模型。
概念解释:
-
预训练: 使用大规模无标注数据先训练一个模型,得到一个泛化的特征提取器或编码器,再应用于下游的特定任务中。
-
经过改编的文本输入: 利用额外的prompt,在输入后面添加额外的提示词或短语,从而将下游任务改编为更贴近预训练任务的形式。如再情感分析任务中在句子后面追加“I feel so [MASK]”转化为词预测任务。
-
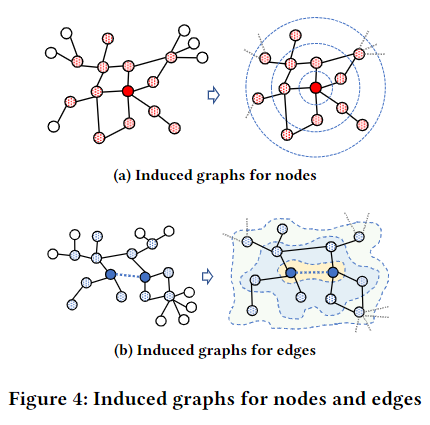
引诱图(induced graph): 指以一点为中心,选择k跳邻居,提取子图,并继承原图中的这些点和边的所有特征
-
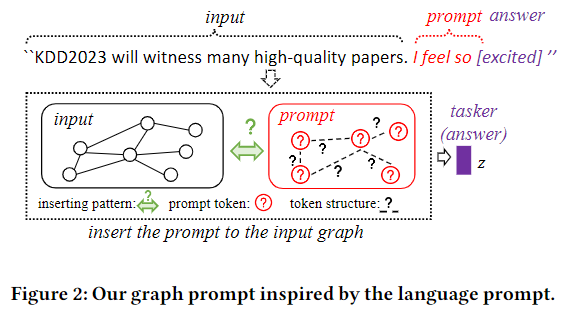
prompt token、token structure、inserting pattern:prompt token是向量化的prompt,token structure表示不同token之间的连接,在language promtp中通常是线性的,graph prompt是非线性的。inserting pattern表示将prompt插入到原始输入中的方式,language里是后面,graph里不定。
这里有个示意图:
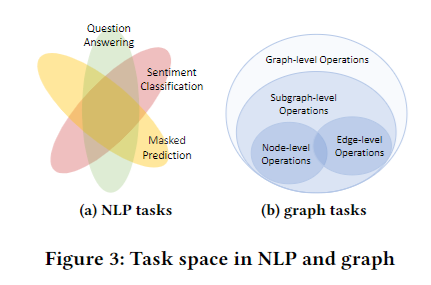
NLP里的大量任务都有共通的部分,因此可以很好地用一个大模型泛化大量任务。而graph的问题中,点和边的问题几乎没有交集,因此作者选用了graph-level的问题作为对齐所有问题的task。
图上的预训练
- 基于节点对比的预训练,如GCA(WWW 2021),通过最大化节点表示的一致性来学习节点特征。
- 基于边预测的预训练
- 基于对比学习的整图预训练,如GraphCL(NIPS 2020),SimGRACE(WWW 2022),通过不同增强的同一图之间表示的一致性来学习整体图知识。
预训练的好处: 利用先验知识降低对label的依赖
预训练的缺陷: 毕竟不是为具体的下游任务设计的,难以有效迁移图知识。
解决方法: 预训练泛化图知识,微调最后一层应用于下游任务。
预训练算法的概括
-
GCA:根据中心性(度、特征向量模长加权度中心性、pagerank,边的中心性取两点均值,最终的分数要取对数做归一,使用时三选一),越不重要的边/点被删去/mask特征的概率越大
- PageRank: \(\sigma = \alpha AD^{-1} \sigma + (1 - \alpha) I\)。其中\(\sigma\)是点的分数,\(\alpha\)是重启概率(阻尼因子),GCA中是0.85,表示随机跳到其他任意点的概率。
-
边预测的预训练:随机游走得到序列,采样点对,有边的正样本,没边的负样本。
-
GraphCL、SimGRACE:前者会使用节点删除、边扰动、属性遮挡和子图提取增强数据集,后者则是不处理数据集直接扰动GNN编码器本身。
存在的问题
希望将提示学习的思想引入图中,实现类似的一个泛化的模型支持多种下游任务。为此需要解释prompt内容、prompt结构组织、prompt插入原图等问题。
整体框架

目标: 学习一个可插入到原图中的提示图,进一步弥合图预训练策略于多个下游任务之间的差距,减轻先验知识到不同域的转移困难。
方法:
1. 统一各种图任务同格式的图级任务
2. 基于统一的图级实例,使用包含科学系token,内部结构和自适应插入模式的提示图,进一步弥合多任务之间的差距
3. 建立元学习过程,学习对多任务设置更加适配的图提示
4. 详细设计prompt图和token、结构和插入模式
5. 引入元学习优化提示图参数
改成图级别任务的原因:
1. 点、边操作是图操作的基本组成
2. 图级别的任务更泛化
3. 整图对比学习模型如GraphCL已经被广泛采用
Prompt Graph
给以graph \(G = (V, E)\),prompt graph\(G_p = (P, S)\),其中\(P =\{p_1, p_2, \dots, p_{|P|}\}\),其中\(p_i \in \mathbb{R}^{1 \times d}\),维度和输入的点特征维度一样,其中\(|P| \ll N\),\(|P| \ll d_h\),\(d_h\)是hidden layer的维度。将prompt加到输入特征上构成prompt特征,再输入预训练模型。\(S\)中保存token之间的连接关系(prompt structre)。
token structure建模方法:
- \(A = \cup^{|P| - 1}_{i = 1, j = i+1}\{a_{ij}\}\),其中\(a_{ij}\)是可调参数(tunable parameter),表示\(p_i\),\(p_j\)的连接概率。
- 直接根据内积判断连接概率
- 直接认为所有token不连接
inserting patterns:
定义插入函数\(\psi\),将\(G_p\)插入到\(G\)中得到改造后的图\(G_m\):
\(\hat{x}_i = x_i + \sum^{|P|}_{k=1}w_{ik}P_k\)
其中\(w_{ik}\)是用于修剪不必要连接的权重:
\(w_{ik} = \left\{ \begin{array}{ll} \sigma(P_k \cdot x^T_i) &,\ if\ \sigma(P_k \cdot x^T_i) \gt \delta \\ 0 &,\ otherwise \\ \end{array} \right.\)
作为替代和特殊情况,也可以使用简化版本:\(\hat{x}_i = x_i + \sum^{|P|}_{k=1}P_k\)
使用Meta Learning的Multi-task Prompting
- 定义任务\(\tau_i\),包含支持集\(D^{s}_{\tau_i}\)和查询集\(D^q_{\tau_i}\)
- 对于图分类,支持集和查询集包含带标签的图,对于点分类,为每个点构建诱导子图,子图标签为目标点的标签。对于边分类,先构建边诱导子图,子图标签为边的标签
- 定义图参数\(\theta\),预训练模型固定参数\(\pi^*\),下游任务参数\(\phi\),将一个任务的pipline定义为\(f_{\theta, \phi|\pi^*}\),使用\(\mathcal{L}_{D}(f)\)作为在数据\(D\)上的\(f\)任务的损失函数,对应参数可以用以下公式更新:\[\theta^k_i = \theta^{k-1}_i - \alpha \nabla_{\theta^{k-1}_i}\mathcal{L}_{D^s_{\tau_i}}(f_{\theta^{k-1}_i, \phi^{k-1}_i|\pi^*}) \\ \phi^k_i = \phi^{k-1}_i - \alpha \nabla_{\phi^{k-1}_i}\mathcal{L}_{D^s_{\tau_i}}(f_{\theta^{k-1}_i, \phi^{k-1}_i|\pi^*}) \]其中\(\theta^0_i = \theta\),\(\phi^0_i=\phi\),元学习的目标函数:\[\theta^*, \phi^* = \arg \min_{\theta, \phi} \sum_{\tau_i \in \mathcal{T}}\mathcal{L}_{D^q_{\tau_i}}(f_{\theta_i, \phi_i|\pi^*}) \]得到元损失后用二阶梯度更新初始的\(\theta, \phi\):\[\begin{align} \theta & \leftarrow \theta - \beta \cdot g^{second}_{\theta}\\ & =\theta - \beta \cdot \sum_{\tau_{i} \in \mathcal{T}} \nabla_{\theta} \mathcal{L}_{D_{q}^{\tau_{i}}}\left(f_{\theta_{i}, \phi_{i} | \pi^{*}}\right) \cdot \nabla_{\theta}\left(\theta_{i}\right)\\ & =\theta - \beta \cdot \sum_{\tau_{i} \in \mathcal{T}} \nabla_{\theta_{i}} \mathcal{L}_{D^{q}_{\tau_{i}}}\left(f_{\theta_{i}, \phi_{i} | \pi^{*}}\right) \cdot\left(I-\alpha H_{\theta}\left(\mathcal{L}_{D^{s}_{\tau_{i}}}\left(f_{\theta_{i}, \phi_{i} | \pi^{*}}\right)\right)\right) \end{align} \]其中\(H_{\theta}(\mathcal{L})\)是Hessian matrix,也就是二阶偏导数矩阵,对于其中的每一个值:\((H_{\theta}(\mathcal{L}))_{ij} = \partial^2\mathcal{L}/\partial\theta_i\theta_j\)。
因此这个式子的意思是:对于每一个任务,计算query data对于该任务而优化的参数的偏导乘以support data对于所有任务的参数的二阶偏导
对于\(\phi\)的更新方式相同。
这里可以看出,supporting data从初始参数出发,更新适配每一个任务的参数模型,而query data用于评估适配后的模型在各任务上的泛化能力,并计算元损失,优化初始参数。
Why It Works?
\(\phi^{*} (A, X + p^{*}) = \phi^{*} (g(A, X)) + O_{p\phi}\)
这段代码是已有工作证明过了的一个结论,其中\(\phi^{*}\)是固定的预训练图模型,\(p^{*}\)是优化后的prompt token,\(g\)是任意图级别的变换,\(O_{p\phi}\)是误差界。也就是说,利用prompt token其实是在模拟图级别变换。
然而,prompt token的质量难以保证,因此作者希望直接通过对图进行扰动来得到最后的结果:
\(\phi^{*} (\psi (G, G^{*}_{p})) = \phi^{*} (g(A, X)) + O^{*}_{p\phi}\)
因为\(\psi\)的操作中同时包含prompt token、token structure和inserting patterns,最终能够得到一个误差更小的结果。
实验
数据集
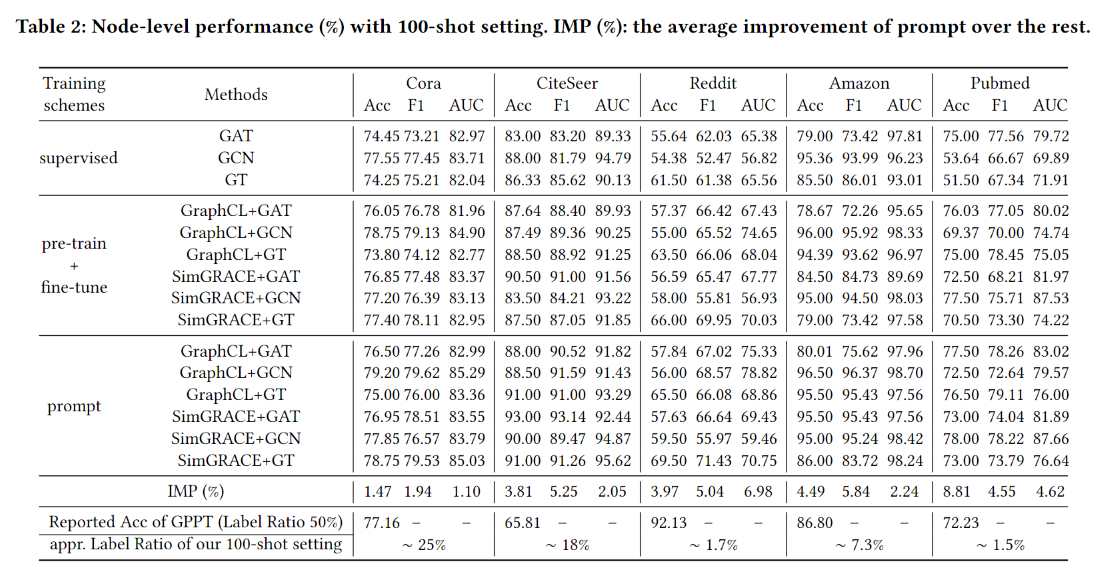
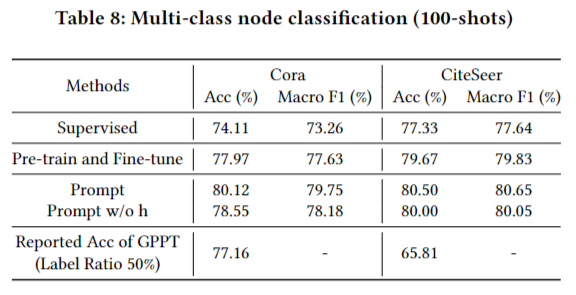
精度实验
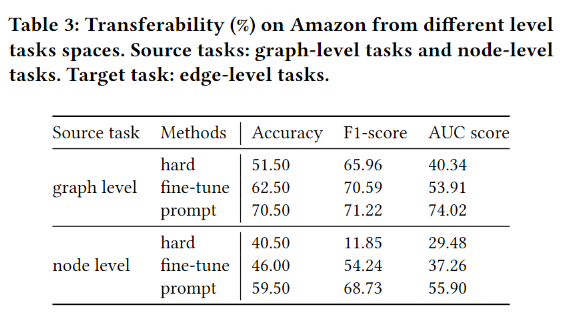
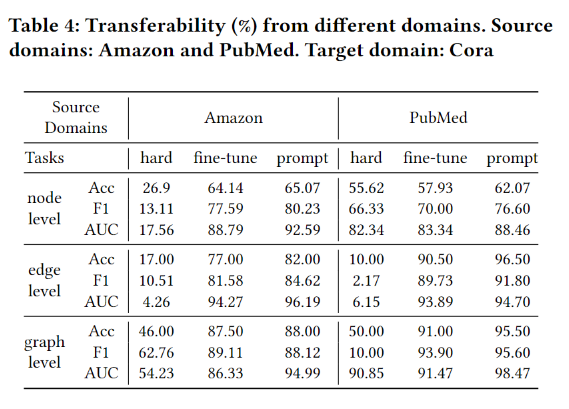
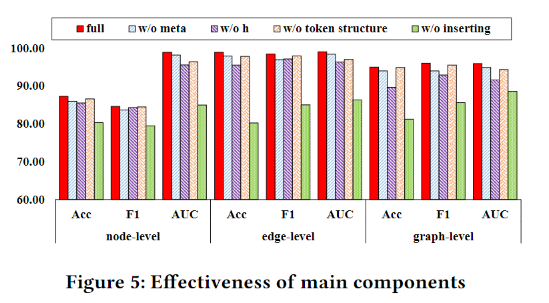
效率实验
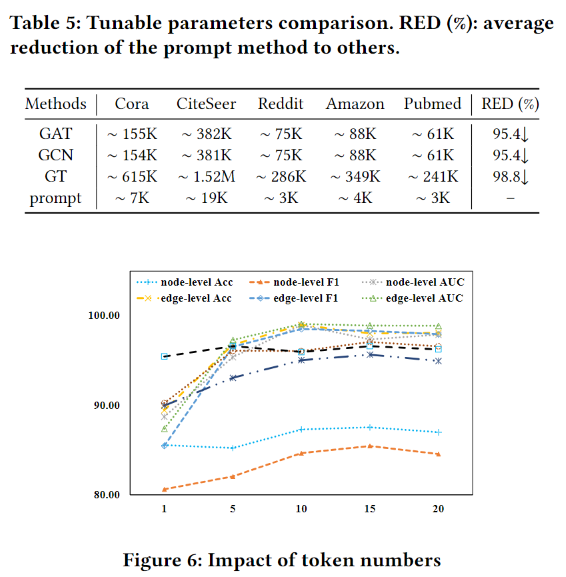
Flexibility

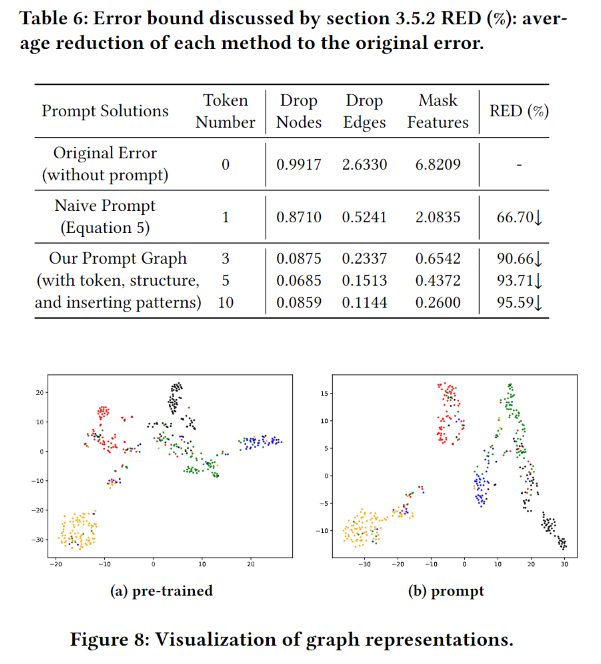
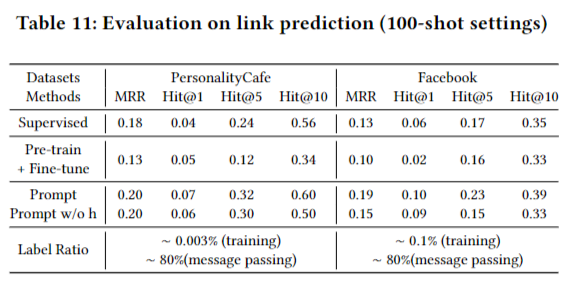
更多的任务测试
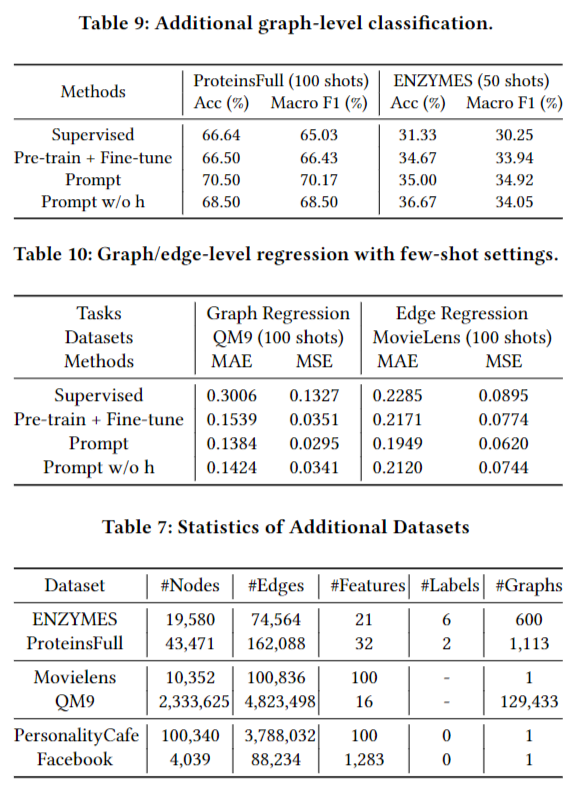
附录
使用海森矩阵(Hessian matrix)实现的二阶优化:
在给出的梯度更新函数中,\(I - \alpha H_{\theta}(\mathcal{L})\)部分涉及到使用单位矩阵减去二阶导数的结果。这个部分可以被理解为对二阶导数进行阻尼修正的一种形式。
通常情况下,二阶优化方法中的更新规则可以表示为:
\(\theta_{\text{new}} = \theta_{\text{old}} - \alpha \cdot H^{-1}_{\theta}(\mathcal{L}) \cdot \nabla_{\theta} \mathcal{L}\)
其中,\(H_{\theta}(\mathcal{L})\)是损失函数\(\mathcal{L}\)关于参数\(\theta\)的海森矩阵,\(\nabla_{\theta} \mathcal{L}\)是损失函数关于参数\(\theta\)的梯度,\(\alpha\)是学习率。
然而,在实际应用中,计算和存储海森矩阵的逆矩阵\(H^{-1}_{\theta}(\mathcal{L})\)的开销很大,并且在某些情况下,海森矩阵可能不是正定的,导致逆矩阵不存在。
为了避免这些问题,可以使用阻尼修正来调整更新步长。其中一种常见的阻尼修正方法是使用单位矩阵减去二阶导数的结果,即\(I - \alpha H_{\theta}(\mathcal{L})\)。这个修正项将二阶导数的影响降低到一阶导数的更新中,起到了一种阻尼的作用。
通过引入阻尼修正项,更新规则可以改写为:
\(\theta_{\text{new}} = \theta_{\text{old}} - \beta \cdot \left(I - \alpha H_{\theta}(\mathcal{L})\right) \cdot \nabla_{\theta} \mathcal{L}\)
其中,\(\beta\)是一个调整阻尼程度的超参数。
这样做的目的是在保持更新步长的方向性的同时,通过调整阻尼因子\(\beta\)来控制更新步长的大小,以避免算法不稳定或发散。
需要注意的是,具体使用哪种阻尼修正方法以及如何选择阻尼因子\(\beta\)取决于具体的应用和算法。在实践中,通常需要进行一些实验和调整来找到合适的超参数值,以获得更好的优化结果。
关于为什么通常形式中采用海森矩阵的逆:
当我们考虑优化问题时,我们希望找到使目标函数(例如损失函数)最小化或最大化的参数值。为了实现这一目标,我们使用梯度和海森矩阵的逆矩阵来指导参数的更新方向。
首先,我们来看一下梯度的含义和推导:
梯度是一个向量,由目标函数关于参数的偏导数组成。对于一个多元函数 \(f(\theta)\),其中 \(\theta\) 是参数向量,梯度表示为 \(\nabla_{\theta} f(\theta)\)。梯度的每个分量表示了函数在对应参数上的变化率。
梯度的方向指示了函数在当前参数点上升或下降最快的方向。因此,我们可以使用梯度的负方向来更新参数,以使函数的值减小。参数的更新公式可以表示为:
\(\theta_{\text{new}} = \theta_{\text{old}} - \alpha \cdot \nabla_{\theta} f(\theta)\)
其中,\(\alpha\) 是学习率,用于控制参数更新的步长。
接下来,我们将介绍海森矩阵的逆矩阵的含义和推导:
海森矩阵是目标函数关于参数的二阶偏导数矩阵。对于一个多元函数 \(f(\theta)\),其中 \(\theta\) 是参数向量,海森矩阵表示为 \(H(\theta)\)。海森矩阵的每个元素是函数的二阶偏导数。
海森矩阵的逆矩阵 \(H^{-1}(\theta)\) 是海森矩阵的逆运算。海森矩阵的逆矩阵在优化算法中常用于调整参数更新的步长,以更快地收敛到最优解。
为了理解为什么海森矩阵的逆矩阵能够更好地表示参数更新方向,我们可以考虑泰勒展开式。泰勒展开式可以将目标函数在某个点处进行局部近似。
复习一下泰勒展开的一般形式:
\(f(x) = f(a) + (x-a)f'(a) + \frac{(x-a)^2}{2!}f''(a) + \frac{(x-a)^3}{3!}f'''(a) + \dots\)
对于一个标量函数 \(f(\theta)\),我们可以使用泰勒展开式来近似函数在参数点 \(\theta_{\text{old}}\) 处的值:
\(f(\theta_{\text{new}}) \approx f(\theta_{\text{old}}) + (\theta_{\text{new}} - \theta_{\text{old}})^T \nabla_{\theta} f(\theta_{\text{old}}) + \frac{1}{2} (\theta_{\text{new}} - \theta_{\text{old}})^T H(\theta_{\text{old}}) (\theta_{\text{new}} - \theta_{\text{old}})\)
这些式子都是最一个向量进行的操作,因此\(\theta\)是个列向量,所以\((\theta_{\text{new}} - \theta_{\text{old}})\)的结果是列向量,需要将他转化为行向量,才能和接下来的求导结果(列向量)相乘。
和泰勒展开的一般形式不同,这边和二阶导相乘的是一次的,这是因为海森矩阵本身就是一个二阶信息矩阵(其中的内容不是数,而是二阶导的公式),因此不需要再对前者进行平方操作。
我们希望找到使得 \(f(\theta_{\text{new}})\) 最小化的参数 \(\theta_{\text{new}}\)。为了实现这一目标,我们可以将上述式子取负号,并忽略高阶项,得到近似的损失函数:
\(\mathcal{L}(\theta_{\text{new}}) \approx -f(\theta_{\text{old}}) - (\theta_{\text{new}} - \theta_{\text{old}})^T \nabla_{\theta} f(\theta_{\text{old}}) - \frac{1}{2} (\theta_{\text{new}} - \theta_{\text{old}})^T H(\theta_{\text{old}}) (\theta_{\text{new}} - \theta_{\text{old}})\)
我们的目标是最小化损失函数 \(\mathcal{L}(\theta_{\text{new}})\)。为了找到最小值,我们可以对损失函数关于参数的偏导数进行求解:
对于 \(\mathcal{L}(\theta_{\text{new}}) \approx -f(\theta_{\text{old}}) - (\theta_{\text{new}} - \theta_{\text{old}})^T \nabla_{\theta} f(\theta_{\text{old}}) - \frac{1}{2} (\theta_{\text{new}} - \theta_{\text{old}})^T H(\theta_{\text{old}}) (\theta_{\text{new}} - \theta_{\text{old}})\),我们将其对 \(\theta_{\text{new}}\) 进行求导。
首先,我们对 \(-f(\theta_{\text{old}})\) 求导,由于 \(\theta_{\text{old}}\) 是常数,导数为零。
然后,我们对 \((\theta_{\text{new}} - \theta_{\text{old}})^T \nabla_{\theta} f(\theta_{\text{old}})\) 求导。这里需要使用矩阵微积分中的链式法则。由于 \(\theta_{\text{old}}\) 是常数,我们可以将 \(\nabla_{\theta} f(\theta_{\text{old}})\) 视为常数向量。因此,对于 \((\theta_{\text{new}} - \theta_{\text{old}})^T \nabla_{\theta} f(\theta_{\text{old}})\) 的导数,我们可以将其视为向量对向量的导数,即 \(\nabla_{\theta_{\text{new}}} [(\theta_{\text{new}} - \theta_{\text{old}})^T \nabla_{\theta} f(\theta_{\text{old}})] = \nabla_{\theta_{\text{new}}} (\theta_{\text{new}} - \theta_{\text{old}})^T \nabla_{\theta} f(\theta_{\text{old}}) = \nabla_{\theta} f(\theta_{\text{old}})\)。
接下来,我们对 \(\frac{1}{2} (\theta_{\text{new}} - \theta_{\text{old}})^T H(\theta_{\text{old}}) (\theta_{\text{new}} - \theta_{\text{old}})\) 求导。
在求导过程中,\(\theta_{\text{new}}^T H \theta_{\text{old}}\) 和 \(\theta_{\text{old}}^T H \theta_{\text{new}}\) 这两项进行了合并,这是因为海森矩阵 \(H\) 是一个对称矩阵,即 \(H = H^T\)。
因此有:
\(\theta_{\text{new}}^T H \theta_{\text{old}} = (\theta_{\text{new}}^T H \theta_{\text{old}})^T = \theta_{\text{old}}^T H^T \theta_{\text{new}} = \theta_{\text{old}}^T H \theta_{\text{new}}\)
两项是完全相同的。
利用矩阵的对称性,我们可以合并这两个相同的项,仅保留其中之一,在求导时就可以一并消去。
可以看到\(\theta_{\text{new}}\)仅出现在第一项和第二项中。
对\(\theta_{\text{new}}\)求导,应用矩阵向量求导法则,有:
因此,对\(\theta_{\text{new}}\)的求导结果为:
\(\frac{\partial}{\partial \theta_{\text{new}}} \left[\frac{1}{2} (\theta_{\text{new}} - \theta_{\text{old}})^T H(\theta_{\text{old}}) (\theta_{\text{new}} - \theta_{\text{old}})\right] = H\theta_{\text{new}} - H\theta_{\text{old}}\)
将以上结果相加,我们得到 \(\nabla_{\theta_{\text{new}}} \mathcal{L}(\theta_{\text{new}}) = -\nabla_{\theta} f(\theta_{\text{old}}) - H(\theta_{\text{old}}) (\theta_{\text{new}} - \theta_{\text{old}})\)。
令上式等于零,我们可以解得:
\(\theta_{\text{new}} = \theta_{\text{old}} - H^{-1}(\theta_{\text{old}}) \nabla_{\theta} f(\theta_{\text{old}})\)
这就是使用海森矩阵的逆矩阵来更新参数的公式。
从使用海森矩阵的逆到使用单位矩阵做差:
首先,我们有原始的更新式 \(\theta_{\text{new}} = \theta_{\text{old}} - H^{-1}(\theta_{\text{old}}) \nabla_{\theta} f(\theta_{\text{old}})\),其中 \(H(\theta_{\text{old}})\) 是海森矩阵。
由于海森矩阵往往是非正定的,且逆运算需要更多额外开销,我们使用近似来替代 \(H^{-1}(\theta_{\text{old}})\)。
我们将其近似为 \(\left(I - \alpha H_{\theta}(\mathcal{L})\right)\),其中 \(H_{\theta}(\mathcal{L})\) 是关于参数 \(\theta\) 的损失函数 \(\mathcal{L}\) 的海森矩阵。能这么干的原因是\(\alpha\)取0时能把式子退化成一阶优化,而保留海森矩阵能增加二阶导数信息。另外,这里使用了差的形式,在保留原本的逆的单调递减的同时,能够更好地限制步长。
接下来,我们引入一个步长参数 \(\beta\),用于控制每次更新的步长大小。
将近似后的海森矩阵逆和步长参数代入原始的更新式,我们得到 \(\theta_{\text{new}} = \theta_{\text{old}} - \beta \cdot \left(I - \alpha H_{\theta}(\mathcal{L})\right) \cdot \nabla_{\theta} \mathcal{L}\)。
这个替代式的原理是通过近似海森矩阵逆来简化计算,并使用步长参数来控制每次更新的步长大小。这种近似可以在实际应用中减少计算复杂度,并在一定程度上保持更新的方向和速度。然而,需要注意的是,这个替代式是一个近似解,可能会引入一定的误差。
- Multi-Task Prompting Networks Neural Graphmulti-task prompting networks neural graph condensation networks neural learning networks neural hello understanding plasticity networks neural networks neural bigdataaiml-ibm-a introduction decoupling networks neural depth powerful networks spectral neural pre-train learning networks neural convolutional networks neural cnn networks learning neural comp