526互联

计算机图形：二维几何变换(2)

发布时间 2023-10-20 22:14:22作者: 明明1109

目录

二维几何变换，分2部分：
计算机图形：二维几何变换(1)
计算机图形：二维几何变换(2) 审核中

平移、旋转、缩放这些属于基本变换，还有一些特殊二维变换如反射、错切。本文讲特殊二维变换。

特殊二维变换

反射

产生对象镜像的变换，称为反射（reflection）。

反射镜像如何得到？
通过将对象绕反射轴旋转180°。反射轴（axis of reflection）可以是xy平面内一条直线，或垂直于xy平面的一条直线。
当反射轴在xy平面内时，绕该轴旋转的路径在垂直于xy平面的平面中；
当反射轴⊥xy平面时，旋转路径在xy平面内。

特殊情况：

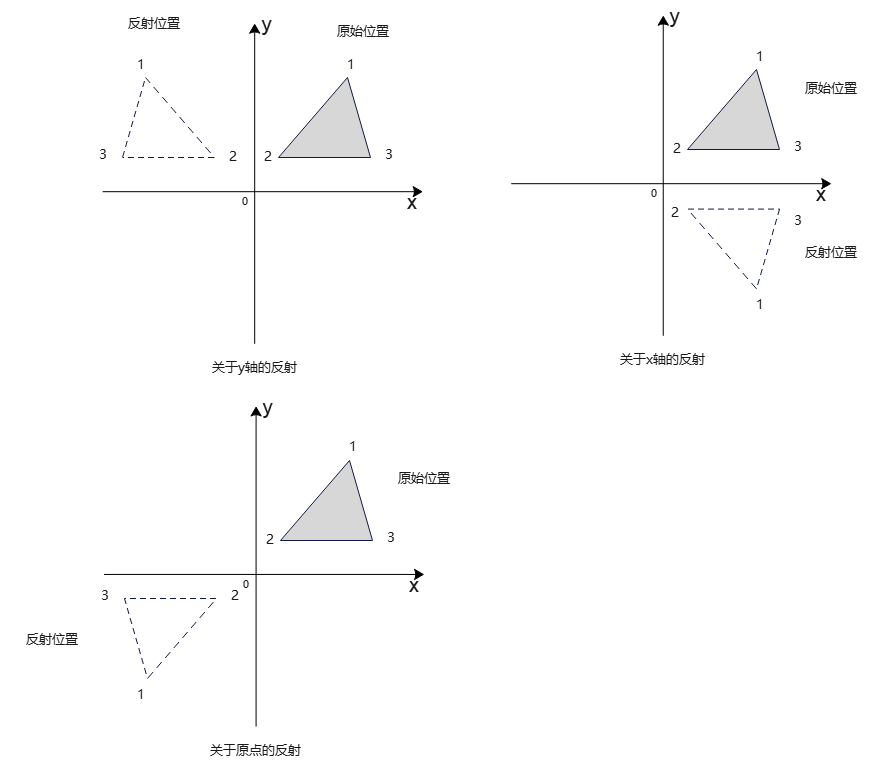
  1. 反射轴是x轴，即直线y=0

x值保持不变，y值为原来反号。于是，反射变换矩阵：

\[\tag{1} \begin{bmatrix} 1 & 0 & 0\\ 0 & -1 & 0\\ 0 & 0 & 1 \end{bmatrix} \]

  1. 反射轴是y轴，即直线x=0

y值保持不变，x值为原来反号。于是，反射矩阵：

\[\tag{2} \begin{bmatrix} -1 & 0 & 0\\ 0 & 1 & 1\\ 0 & 0 & 1 \end{bmatrix} \]

  1. 同时翻转x、y坐标，即相对于原点的反射

反射矩阵：

\[\tag{3} \begin{bmatrix} -1 & 0 & 0\\ 0 & -1 & 0\\ 0 & 0 & 1 \end{bmatrix} \]

相当于θ=180°的旋转矩阵R(θ)，即将xy平面内的对象绕原点旋转180°。

关于y轴、x轴、原点反射示意图：

  1. 反射轴为直线y=x

反射矩阵：

\[\tag{4} \begin{bmatrix} 0 & 1 & 0\\ 1 & 0 & 0\\ 0 & 0 & 1 \end{bmatrix} \]

两种方法：
Ⅰ 根据y=x对称性

任一点(x,y)关于y=x对称点为(y,x)，于是

\[y'=x\\ x'=y \]

可得变换矩阵。

Ⅱ 复合变换

分三步：
①将直线y=x顺时针旋转45°（θ=45°），到x轴上，变换矩阵R(-θ)；
②按x轴反射，变换矩阵\(R_{y=0}\)（式(1)）；
③逆时针旋转45°，将直线y=x旋转回原始位置，变换矩阵R(θ)。

复合变换矩阵：

\[\tag{5} \begin{bmatrix} 0 & 1 & 0\\ 1 & 0 & 0\\ 0 & 0 & 1 \end{bmatrix} \]

  1. 关于任意直线y=mx+b的反射

可以用平移-旋转-反射的复合变换来完成：
先平移到经过原点，再旋转到x轴，进行x轴反射，最后逆旋转、逆平移回原位置。

错切

错切（shear）是一种使对象形状发生变化的变换，经过错切的对象好像是由已经相互滑动的内部夹层组成。

2种常用错切：
1）移动x坐标值的错切；
2）移动y坐标值的错切。

  • 相对于x轴的x方向错切

变换矩阵：

\[\tag{6} \begin{bmatrix} 1 & sh_x & 0\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{bmatrix} \]

对应坐标变换：

\[\tag{7} x'=x+sh_x\cdot y, y'=y \]

\(sh_x\)可以是任意实数。

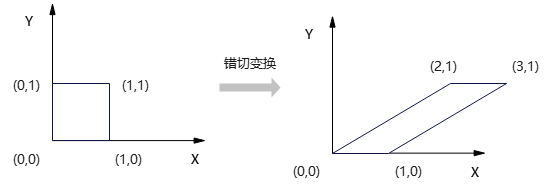
例，\(sh_x=2\)，正方形错切变换成平行四边形，如下图：

  • 相对于其他参考线的x方向错切

错切矩阵：

\[\tag{8} \begin{bmatrix} 1 & sh_x & -sh_x\cdot y_{ref}\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{bmatrix} \]

对应坐标变换：

\[\tag{9} x'=x+sh_x(y-y_{ref}), y'=y \]

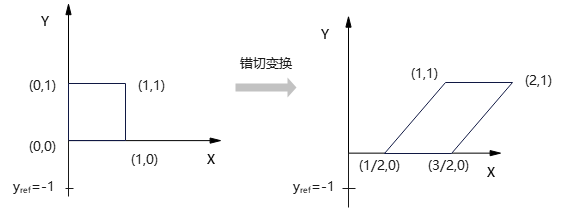
例，错切参数\(sh_x={1\over 2}\)、相对于直线\(y_{ref}=-1\)的错切：

  • 相当于\(x=x_{ref}\)的y方向错切

错切矩阵：

\[\tag{10} \begin{bmatrix} 1 & 0 & 0\\ sh_y & 1 & -sh_y\cdot x_{ref}\\ 0 & 0 & 1 \end{bmatrix} \]

对应坐标变换：

\[\tag{11} x'=x, y'=y+sh_y(x-x_{ref}) \]

小结

错切能将正方形变换成梯形，这在后面的透视投影的斜透视投影棱台中会有应用。