https://blog.csdn.net/weixin_45697774/article/details/104274160
知识

需要注意的是,\(P(A|B)P(B)=P(AB)\),这个东西并没有要求 \(A,B\) 独立。感性理解一下,两件事情同时发生即在发生事件 \(B\) 的情况下,发生 \(A\),若没发生 \(A\),则显然 A,B 不可能同时发生。显然这个式子等价于 \(P(B|A)P(A)\),即在发生 \(A\) 的情况下,发生 \(B\),同样也是 \(A,B\) 同时发生。

期望的线性性证明。
其中一步挺重要的。
最后一步是因为 \(\sum\limits_{y}P(Y=y|X=x)=1\),即在事件 \(X\) 发生 \(x\) 下 \(Y\) 事件无论发生啥,所有概率和一定为 \(1\)。
同理,另一部也可证明。
注意到,我们并没有利用到两个事件的独立性,因此 \(X,Y\) 之间可以不独立。
期望 dp
首先,往往是设 \(f(x)\) 为从 \(x\) 出发的期望。
然后转移利用全期望公式。

即枚举下一步的事件,然后其期望已经求好了,乘上其概率即可。
但在 [PKUWC2018]随机游走 中,存在 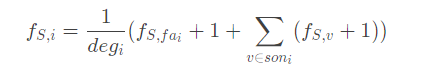
这个 \(+1\) 是为什么呢?
感谢 wxy 老师的教导。
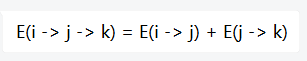
考虑我们求得是 \(E(X|Y=y)\),即下一步走到某个点,当前节点的期望。
考虑 \(E(Y=y)\) 那么一定是 \(\sum\limits_i p_i v_i\) 的形式,现在多走了一步,那么一定是 \(\sum_i p_i(v_i+1)=\sum\limits_i p_iv_i+\sum\limits_i p_i=E(Y=y)+1\)。
同理,你也可以用期望的线性性来解决。
原先的东西你可以看成是 \(x\to n\),那么你钦定 \(y\),变成了在从 \(x\) 走到 \(y\) 的情况下,求 \(E(x\to y\to n)=E(x\to y)+E(y\to n)=1+E(y\to n)\)。
CF280C Game on Tree
我认为题解大多都很抽象。
考虑本质上是在干什么,求操作次数的期望。
那我本质上是不是可以看成,有一个排列,这个排列钦定的是操作顺序,你需要按照这个操作顺序去染色,当然,有些点可能到它的时候没得染,然后你要通过所有的排列来求出本质不同的染色方案,仅此而已。
那么,题目求得即 \(E(\sum_i [i 在其所有祖先前操作])=\sum_i E([i在其所有的祖先前操作])=\sum_i P(i在其所有的祖先前操作)\),至此我们已分离出每一个点。
考虑单独求出来,既然要求 \(i\) 在其所有的祖先前操作,则要求 \(i\) 在排列中的顺序先于其祖先,设共 \(m\) 个点。即总方案数 \(m!\),其中固定住 \(i\) 在第一位,则有 \((m-1)!\),即概率为 \(\dfrac{(m-1)!}{m!}=\dfrac{1}{m}\),然后直接相加起来即可。