[HNOI2016] 网络
题目描述
一个简单的网络系统可以被描述成一棵无根树。每个节点为一个服务器。连接服务器与服务器的数据线则看做一条树边。两个服务器进行数据的交互时,数据会经过连接这两个服务器的路径上的所有服务器(包括这两个服务器自身)。
由于这条路径是唯一的,当路径上的某个服务器出现故障,无法正常运行时,数据便无法交互。此外,每个数据交互请求都有一个重要度,越重要的请求显然需要得到越高的优先处理权。现在,你作为一个网络系统的管理员,要监控整个系统的运行状态。系统的运行也是很简单的,在每一个时刻,只有可能出现下列三种事件中的一种:
- 在某两个服务器之间出现一条新的数据交互请求;
- 某个数据交互结束请求;
- 某个服务器出现故障。系统会在任何故障发生后立即修复。也就是在出现故障的时刻之后,这个服务器依然是正常的。但在服务器产生故障时依然会对需要经过该服务器的数据交互请求造成影响。
你的任务是在每次出现故障时,维护未被影响的请求中重要度的最大值。注意,如果一个数据交互请求已经结束,则不将其纳入未被影响的请求范围。
输入格式
第一行两个正整数 \(n,m\),分别描述服务器和事件个数。服务器编号是从 \(1\) 开始的,因此 \(n\) 个服务器的编号依次是 \(1,2,3,\cdots,n\)。
接下来 \(n-1\) 行,每行两个正整数 \(u,v\),描述一条树边。\(u\) 和 \(v\) 是服务器的编号。
接下来 \(m\) 行,按发生时刻依次描述每一个事件;即第 \(i\) 行(\(i=1,2,3,...,m\))描述时刻 \(i\) 发生的事件。每行的第一个数 \(\mathrm{type}\) 描述事件类型,共 \(3\) 种类型:
- 若 \(\mathrm{type}=0\),之后有三个正整数 \(a,b,v\),表示服务器 \(a,b\) 之间出现一条重要度为 \(v\) 的数据交互请求;
- 若 \(\mathrm{type}=1\),之后有一个正整数 \(t\),表示时刻 \(t\)(也就是第 \(t\) 个发生的事件)出现的数据交互请求结束;
- 若 \(\mathrm{type}=2\),之后有一个正整数 \(x\),表示服务器 \(x\) 在这一时刻出现了故障。
对于每个 \(\mathrm{type}\) 为 \(2\) 的事件,就是一次询问,即询问“当服务器 \(x\) 发生故障时,未被影响的请求中重要度的最大值是多少?”注意可能有某个服务器自身与自身进行数据交互的情况。\(2 \le n \le 10^5\),\(1 \le m \le 2\times 10^5\),其他的所有输入值不超过 \(10^9\)。
输出格式
对于每个 \(\mathrm{type}=2\) 的事件,即服务器出现故障的事件,输出一行一个整数,描述未被影响的请求中重要度的最大值。如果此时没有任何请求,或者所有请求均被影响,则输出 \(-1\)。
样例 #1
样例输入 #1
13 23
1 2
1 3
2 4
2 5
3 6
3 7
4 8
4 9
6 10
6 11
7 12
7 13
2 1
0 8 13 3
0 9 12 5
2 9
2 8
2 2
0 10 12 1
2 2
1 3
2 7
2 1
0 9 5 6
2 4
2 5
1 7
0 9 12 4
0 10 5 7
2 1
2 4
2 12
1 2
2 5
2 3
样例输出 #1
-1
3
5
-1
1
-1
1
1
3
6
7
7
4
6
提示
样例给出的树如下所示:
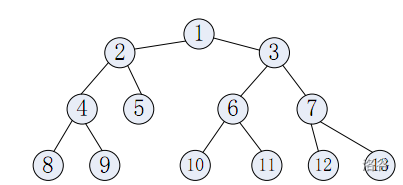
解释其中的部分询问;下面的解释中用 \((a,b;t,v)\) 表示在 \(t\) 时刻出现的服务器 \(a\) 和 \(b\) 之间的重要度为 \(v\) 的请求:
对于第一个询问(在时刻 \(1\)),此时没有任何请求,输出 \(-1\)。
对于第四个询问(在时刻 \(6\)),此时有两条交互\((8,13;2,3),(9,12;3,5)\),所有询问均经过 \(2\) 号服务器,输出 \(-1\)。
对于第五个询问(在时刻 \(8\)),此时有三条交互 \((8,13;2,3),(9,12;3,5),(10,12;7,1)\),只有交互 \((10,12;7,1)\) 没有经过 \(2\) 号服务器,因此输出其重要度 \(1\)。
对于最后一个询问(在时刻 \(23\)),此时有三条交互 \((9,5;12,6),(9,12;16,4),(10,5;17,7)\)。当 \(3\) 号服务器出现故障时,只有交互 \((9,5;12,6)\) 没有经过 \(3\) 号服务器,因此输出 \(6\)。
\(\text{upd 2016.5.20}\):新加一组 \(\text{Hack}\) 数据。
考虑二分答案,现在要求是否所有的经过权值超过 md 的点都经过 \(x\)
离散化,注意要把所有权值离散化成互不相同的数,方便删除。
维护权值线段树,每个节点维护权值在这个区间内的所有链的链交。容易发现,链的链交要不不存在,要不也是一条链。可以用线段树维护。
然后在线段树上二分即可。如果用 \(O(1)\) lca 的话,总复杂度 \(O(q\log q)\)。
这里写一下求链交的方法。
要求 \((a,b)\) 和 \((c,d)\) 的链交,先找到 \(lca(a,c),lca(a,d),lca(b,c),lca(b,d)\) 中深度较大的两个点(深度一样任取),设为 \(e\) 和 \(f\).
如果 \(e\ne f\),那么链交就是 \((e,f)\)。
否则如果 \(e\) 的深度等于 \(lca(a,b),lca(c,d)\) 的最大深度,链交依然为 \(e,f\)。
否则链交不存在。
#include<bits/stdc++.h>
using namespace std;
const int N=2e5+5;
int n,m,lg[N],idx,in[N],k,lsh[N],mp[N],dep[N],op[N],a[N],b[N],v[N];
pair<int,int>tr[N<<2];
vector<int>g[N];
struct node{
int mn,wh;
node operator+(const node&n)const{
return mn<n.mn? (node){mn,wh}:n;
}
}st[20][N];
int lca(int x,int y)
{
if(in[x]>in[y])
swap(x,y);
int k=lg[in[y]-in[x]+1];
return (st[k][in[x]]+st[k][in[y]-(1<<k)+1]).wh;
}
pair<int,int>mge(pair<int,int>u,pair<int,int>v)
{
if(!u.first||!v.first)
return make_pair(0,0);
if(u.first==-1)
return v;
if(v.first==-1)
return u;
int p1=lca(u.first,v.first);
int p2=lca(u.first,v.second);
int p3=lca(u.second,v.first);
int p4=lca(u.second,v.second);
int f0=p1,f1=0;
if(dep[p2]>dep[f0])
f1=f0,f0=p2;
else if(dep[p2]>dep[f1])
f1=p2;
if(dep[p3]>dep[f0])
f1=f0,f0=p3;
else if(dep[p3]>dep[f1])
f1=p3;
if(dep[p4]>dep[f0])
f1=f0,f0=p4;
else if(dep[p4]>dep[f1])
f1=p4;
// printf("%d %d\n`",f0,f1);
if(f1^f0||dep[f0]==max(dep[lca(u.first,u.second)],dep[lca(v.first,v.second)]))
return make_pair(f0,f1);
return make_pair(0,0);
}
void yu(int x,int y)
{
dep[x]=dep[y]+1;
st[0][in[x]=++idx]=(node){dep[x],x};
for(int v:g[x])
if(v^y)
yu(v,x),st[0][++idx]=(node){dep[x],x};
}
void build(int o,int l,int r)
{
tr[o]=l? make_pair(-1,-1):make_pair(0,0);
if(l==r)
return;
int md=l+r>>1;
build(o<<1,l,md);
build(o<<1|1,md+1,r);
}
void upd(int o,int l,int r,int x,pair<int,int>p)
{
if(l==r)
{
tr[o]=p;
return;
}
int md=l+r>>1;
if(md>=x)
upd(o<<1,l,md,x,p);
else
upd(o<<1|1,md+1,r,x,p);
tr[o]=mge(tr[o<<1],tr[o<<1|1]);
}
int ask(int o,int l,int r,pair<int,int>p)
{
if(l==r)
{
// printf("qzm:%d %d %d %d %d\n",l,tr[o].first,tr[o].second,mge(tr[o],p).first);
return l;
}
int md=l+r>>1;
if(mge(tr[o<<1|1],p).first)
return ask(o<<1,l,md,p);
return ask(o<<1|1,md+1,r,p);
}
int main()
{
for(int i=2;i<N;i++)
lg[i]=lg[i>>1]+1;
scanf("%d%d",&n,&m);
for(int i=1,u,v;i<n;i++)
scanf("%d%d",&u,&v),g[u].push_back(v),g[v].push_back(u);
yu(1,0);
for(int i=1;i<20;i++)
for(int j=1;j+(1<<i)-1<=idx;j++)
st[i][j]=st[i-1][j]+st[i-1][j+(1<<i-1)];
for(int i=1;i<=m;i++)
{
scanf("%d%d",op+i,a+i);
if(!op[i])
{
scanf("%d%d",b+i,v+i);
lsh[++k]=v[i];
}
}
sort(lsh+1,lsh+k+1);
lsh[0]=-1;
build(1,0,k);
pair<int,int>h=mge(make_pair(2,2),make_pair(9,12));
// printf("%d\n",lca(9,2));
// printf("%d %d\n",h.first,h.second);
// exit(0);
for(int i=1;i<=m;i++)
{
if(!op[i])
{
v[i]=lower_bound(lsh+1,lsh+k+1,v[i])-lsh;
++mp[v[i]];
v[i]+=mp[v[i]]-1;
upd(1,0,k,v[i],make_pair(a[i],b[i]));
}
else if(op[i]^2)
upd(1,0,k,v[a[i]],make_pair(-1,-1));
else
printf("%d\n",lsh[ask(1,0,k,make_pair(a[i],a[i]))]);
}
}