2023-06-16《计算方法》- 陈丽娟 - 插值法(一)
本章给出了一些基本的插值法理论和算法,附带解决部分习题。
一、拉格朗日插值
为了直观,这里部分符号和书中不一致,但是得到的形式更优美。
1. 一次拉格朗日插值
在给定区间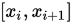 上,已知
上,已知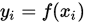 ,
, 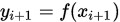 , 一次拉格朗日插值要求插值函数
, 一次拉格朗日插值要求插值函数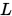 满足
满足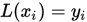 ,
,  .
.
由两点确定一条直线,显然可以得到如下的一个可行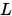
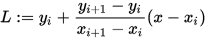
改写为两点式,可得

上述函数可以看作是
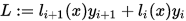
其中
 称为线性插值基函数,且满足
称为线性插值基函数,且满足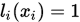 ,
,  ,
, 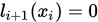 , 和
, 和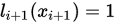 .
.
2. 二次拉格朗日插值
根据上述一次拉格朗日插值方法,我们可以构建对于3个点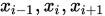 和对应值
和对应值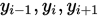 的二次拉格朗日插值法。
的二次拉格朗日插值法。
首先给出二次拉格朗日插值线性插值基函数的条件:
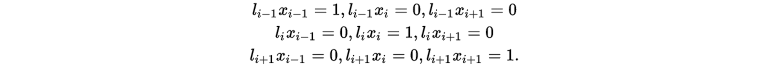
由于三个点可以确定一条二次函数,设
 , 可以分别得到
, 可以分别得到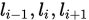 为
为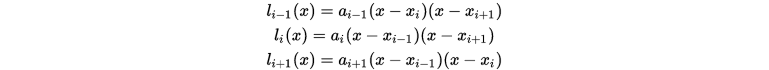
注意到
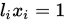 , 带入上式可得
, 带入上式可得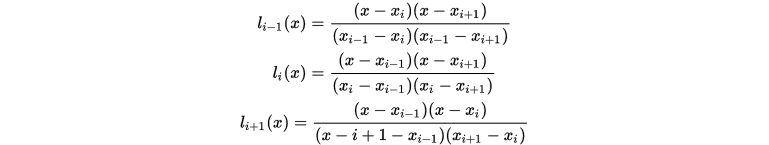
立即可得到二次拉格朗日插值公式

3. 多次拉格朗日插值
下面直接给出多次拉格朗日插值法的形式。
对于一个含有n个点 和对应的值
和对应的值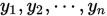 的拉格朗日插值问题,我们有下述解析函数
的拉格朗日插值问题,我们有下述解析函数

其中
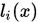 定义为(拉格朗日插值基函数)
定义为(拉格朗日插值基函数)
- 唯一性定理
- 在次数不超过
 的几何多项式
的几何多项式 中,满足插值条件的插值多项式
中,满足插值条件的插值多项式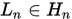 是存在的,且是唯一的。
是存在的,且是唯一的。
证明: 存在性由拉格朗日插值法可得。唯一性可假设存在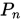 是另一个满足条件的多项式,则
是另一个满足条件的多项式,则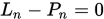 对所有
对所有 个点成立,但由
个点成立,但由 次多项式最多只有
次多项式最多只有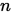 个根得到矛盾。
个根得到矛盾。
最后在本节我们给出拉格朗日插值的Matlab程序:
- % 拉格朗日插值,传入x_i, y_i, 和待求点x,返回x对应的插值和系数Lx
- function [y Lx] = LagInsert(x, xi, yi)
- %若x是数组,则对每个x返回值,以及系数组(如果需要返回的矩阵太大,则不返回)
- Lx = [];
- y = 0;
- n = length(xi);
- isReturnLx = true;
- if n * length(x) > 1e5
- isReturnLx = false;
- end
- for i = 1:n
- lx = 1;
- for j = 1:n
- if j ~= i
- lx = lx .* (x - xi(j))/ (xi(i) - xi(j));
- end
- end
- y = y + lx * yi(i);
- if isReturnLx
- Lx = [Lx;lx];
- end
- end
- end
对 进行测试
进行测试
- xi = 1:10;
- yi = sin(xi);
- x = 0:0.1:10;
- [y Lx] = LagInsert(x, xi, yi);
- plot(x,y)
- hold on
- scatter(xi,yi)
得到结果

书中也有拉格朗日插值的代码,处理上有些微不同。
二、差商与牛顿插值
拉格朗日插值当插值点增加或者减少时,需要重新开始所有计算,牛顿法可以解决这个问题。
考虑对于 个点的
个点的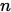 次多项式插值:
次多项式插值:

首先给出差商的定义:
- 差商
- 函数
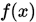 关于点
关于点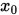 ,
, 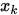 的一阶差商
的一阶差商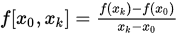 ; 关于
; 关于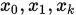 的二阶差商
的二阶差商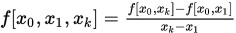 ; 以及
; 以及 阶差商
阶差商

不知怎么的#F44336反正就有
- 差商与节点的位置无关

- 注意到位置无关性和差商定义,有

- 差商与导数之间的关系

- 若
 , 则
, 则 .
. - 若
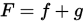 , 则
, 则 .
.
差商的计算-- 差商表。注意差商表中比如第四行第三列的计算方式为
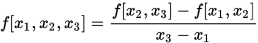

我们给出差商表的计算程序:
- %根据一组数据,计算对应的差商表(differience quotients)
- function [dq] = DQ(x, fx, dq)
- %x 是横坐标值
- %fx 是对应的函数值
- %首先判断dq是否是一张dq表
- if length(dq) == 1
- n = length(x);
- dq = zeros(n, n);
- dq(:,1) = fx;
- for i = 2:n %列
- for j = i:n %行
- dq(j,i) = (dq(j,i-1) - dq(j-1,i-1))/(x(j)-x(j-i+1));
- end
- end
- else
- %在表后面添加值
- m = length(dq);
- n = length(x);
- dq_temp = dq;
- dq = zeros(n,n);
- dq(1:m,1:m) = dq_temp;
- dq(:,1) = fx;
- for i = 2:n
- for j = (max(m,i)):n
- dq(j,i) = (dq(j,i-1) - dq(j-1,i-1))/(x(j)-x(j-i+1));
- end
- end
- end
- end
该算法可以处理当差商表存在时快速计算新加入的点的差商。
得到差商表后,我们可以根据下述牛顿插值法:

结合差商程序,我们给出下列牛顿插值法的程序:
- function [NI] = NewtonInsert(tx, x, fx, dq)
- %计算dq表
- [dq] = DQ(x, fx, dq);
- %计算插值的结果, 可以是向量
- NI = dq(1,1);
- for i = 2:length(dq)
- tq = 1;
- for j = 1:(i-1)
- tq = tq .* (tx-x(j));
- end
- NI = NI + dq(i,i) * tq;
- end
- end
最后依然给出实例代码:
- % 测试生成的差商表
- x = 1:10;
- fx = sin(x);
- [dq] = DQ(x, fx, 1);
- % 增加x的数量
- y = [x x+0.1];
- fy = sin(y);
- tx = (-1):0.1:10;
- [NI1] = NewtonInsert(tx, x, fx, dq);
- [NI2] = NewtonInsert(tx, y, fy, dq);
- plot(tx,NI1)
- hold on
- plot(tx, NI2)
- hold on
- scatter(x, fx)
插值结果如下图所示

可以看到在插值区间内的拟合效果很好,但是在插值区间外没有限制。