1. 机器学习定义
Field of study that gives computers the ability to learn without being explicitly programmed. -- Arthur Samuel(1959)
如果只能进行少数训练,该模型将比同等情况下,进行大量训练的表现更差。
机器学习最常用的两种类型:
- 监督学习(Supervised Learning)
现实世界中应用最为广泛,涵盖于本课程第一、第二部分 - 非监督学习(Unsupervised Learning)
涵盖于本课程第三部分 - 强化学习(Reinforcement Learning)
本课程暂不多作介绍。
2. 监督学习
监督学习的关键特征是给予学习算法一些示例去学习,包括正确的和错误的示例。

2.1 回归(Regression)
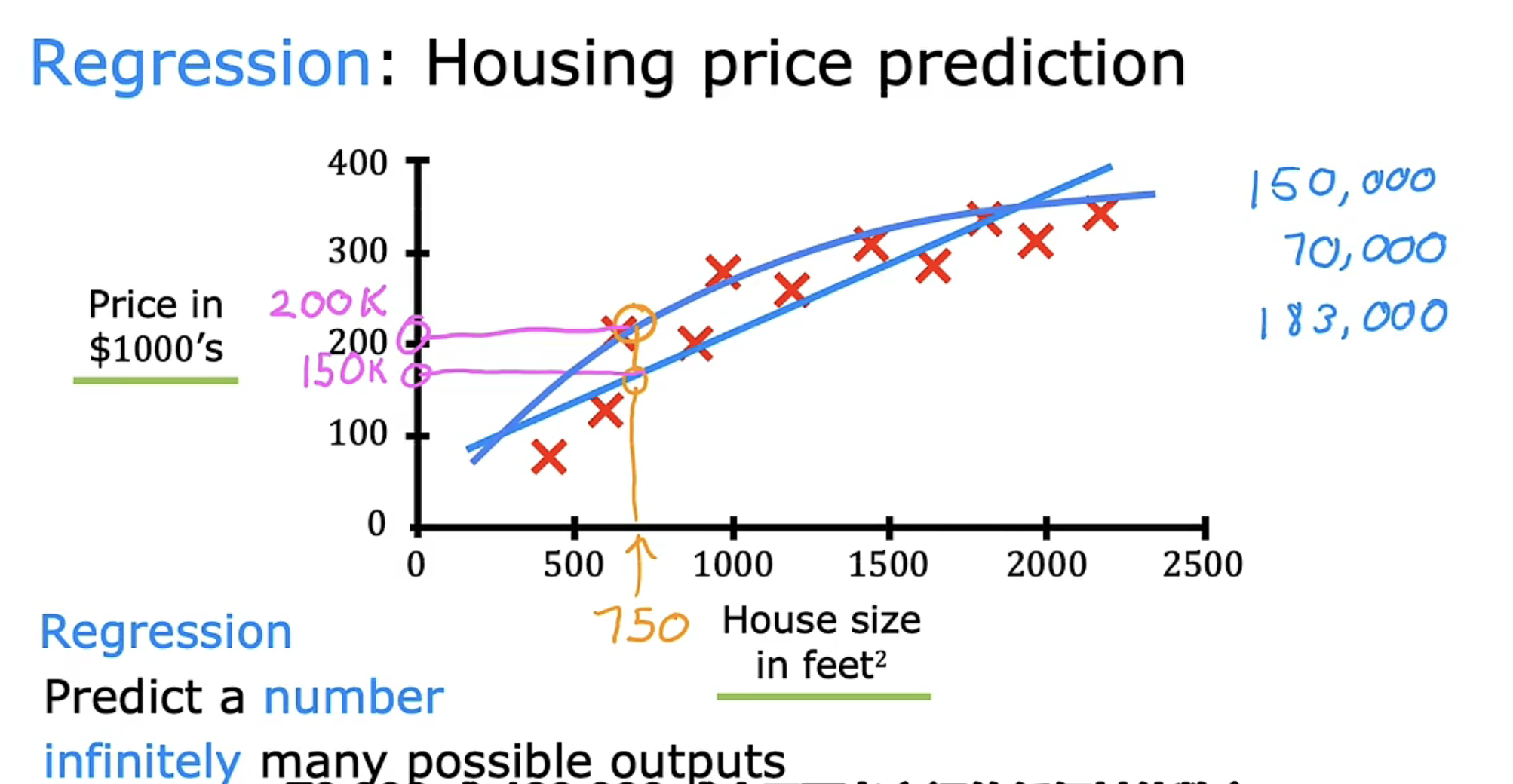
根据图中所展示的相应数据点,简单粗暴给出一条拟合的直线也能给出预测。
但若是能够拟合一条曲线,相比于直线能更符合现有数据的表现,即预测的 label 会更加精确。
因此对于回归问题,我们需要决定是拟合直线、曲线、还是一些更复杂的其他函数。
- 我们可以理解监督学习:
learn to predict input, output or X to Y mapping. - 我们可以定义回归:
Regression: Predict a number out of infinitely many possible outputs.
2.2 分类(Classification)
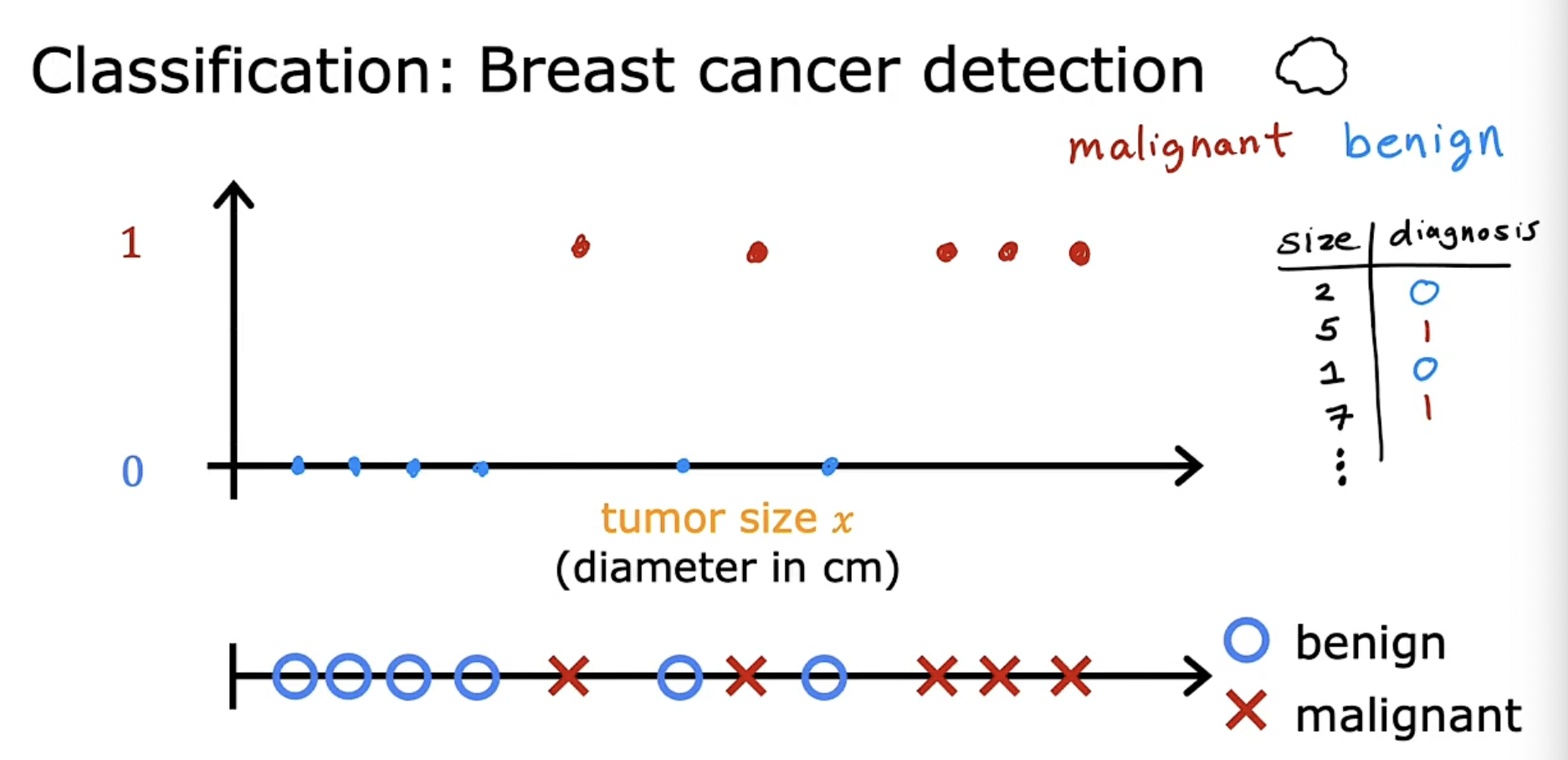
示例的肿瘤检测,是一个二分类问题,即只需要判断为 0/1,代表良性/恶性。
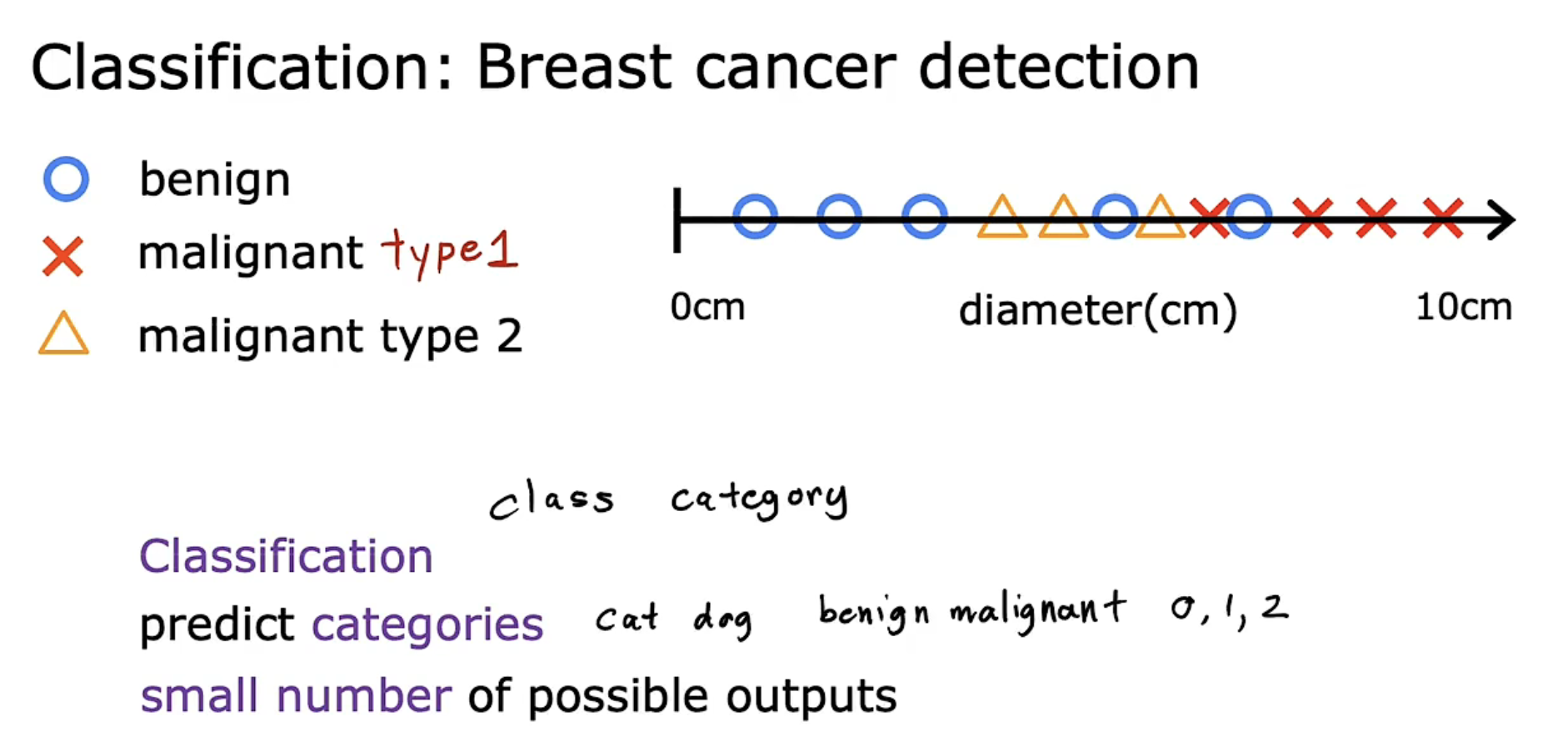
以此进行推广,我们可以判断一个多分类问题,在此处为判断 0/1/2。
上述例子只使用了一个特征,我们可以使用更多的输入值(two or more inputs)进行判断,如添加年龄属性。
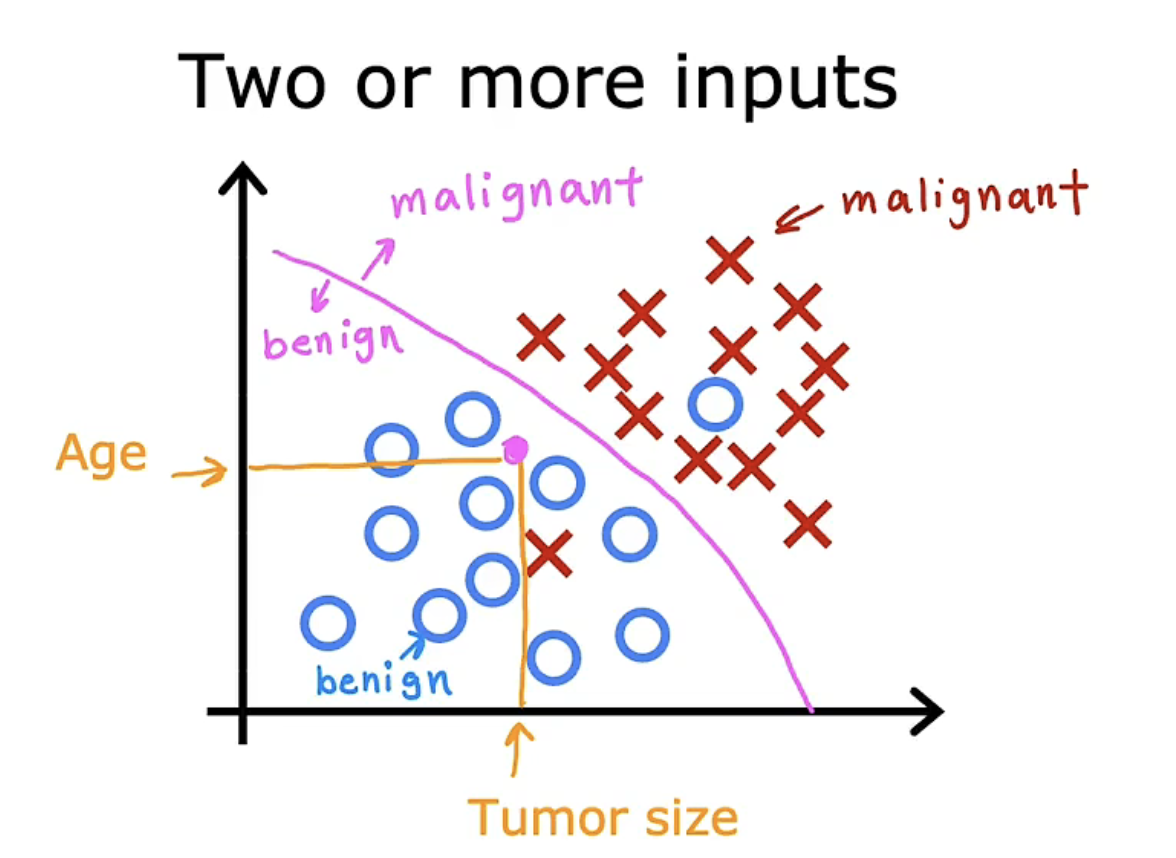
现实生活中我们处理分类问题时,往往需要使用许多特征(inputs)进行判断。
- 我们可以定义分类:
Classification: predict categories which can be small finite number of possible outputs
2.3 小结

3. 非监督学习(Unsupervised Learning)
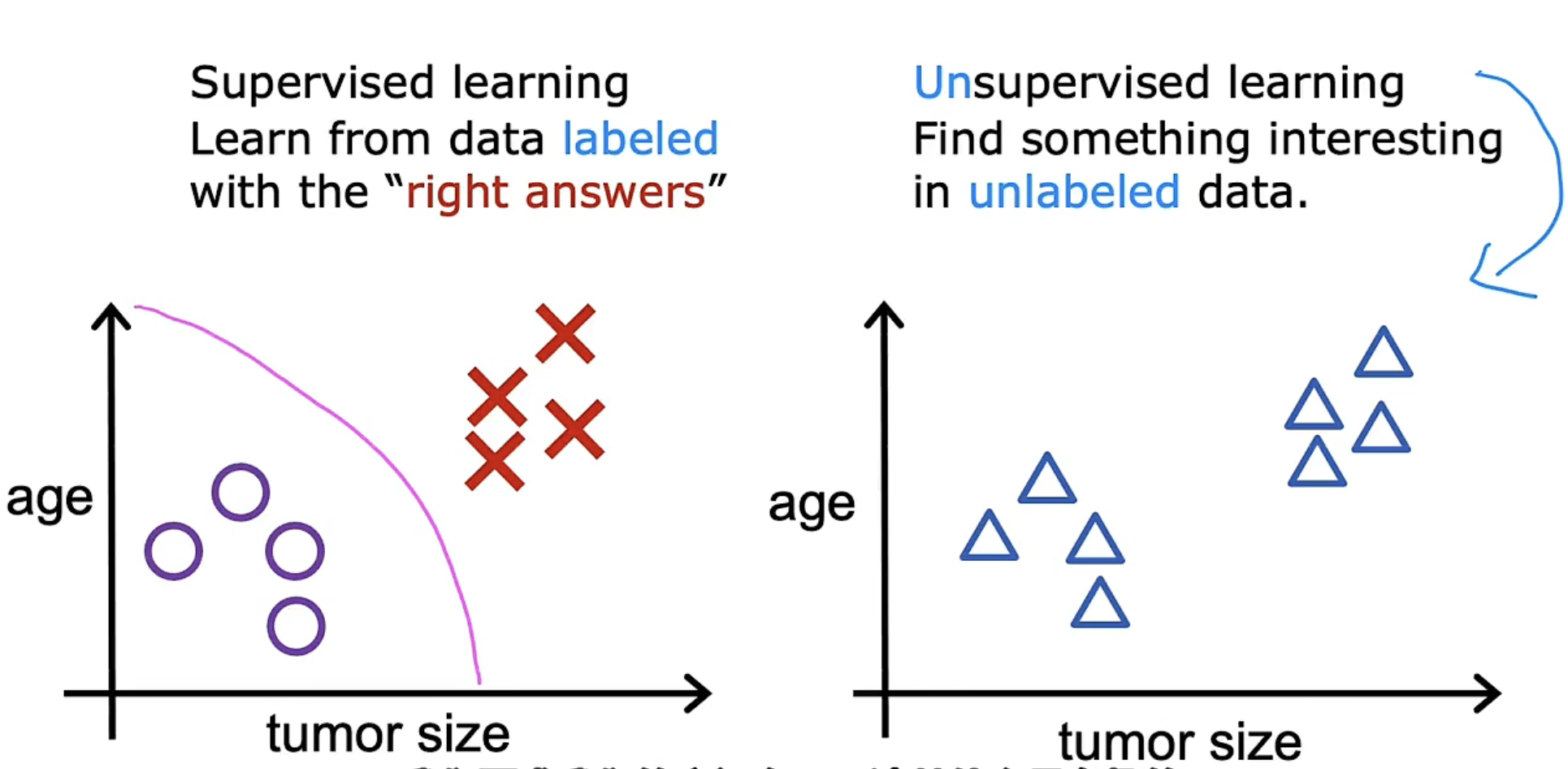
对于监督学习,相应的数据集中我们可以得到每条样例数据对应的标签(label);而在非监督学习中,不存在这样一个标签(label)。
这意味着我们可能需要使用算法去自行寻找一个标签,或者我们可以使用样例数据进行探索,自行发现规律。
3.1 聚类(Clustering)
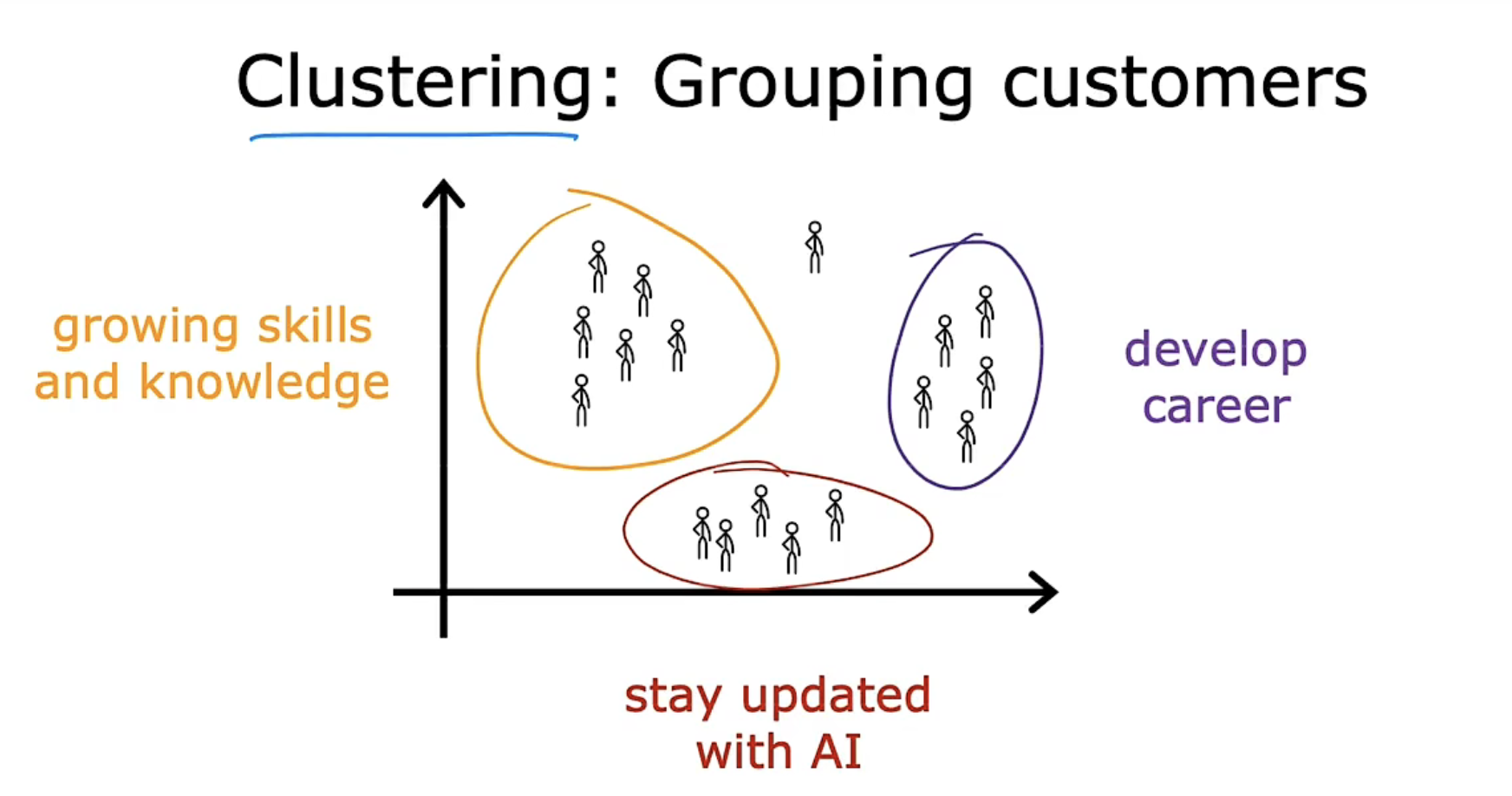
聚类是获取没有标签的数据集,并尝试将它们自动分组到集群中。
如图所示,我们可能可以将顾客划分为三类群体。
3.2 另两种非监督学习方法

- 聚类(Clustering)
Group similar data points together. - 异常检测(Anomaly Detection)
Find unusual data points. - 降维(Dimensionality reduction)
Compress data using fewer numbers.
4. 线性回归(Linear Regression)
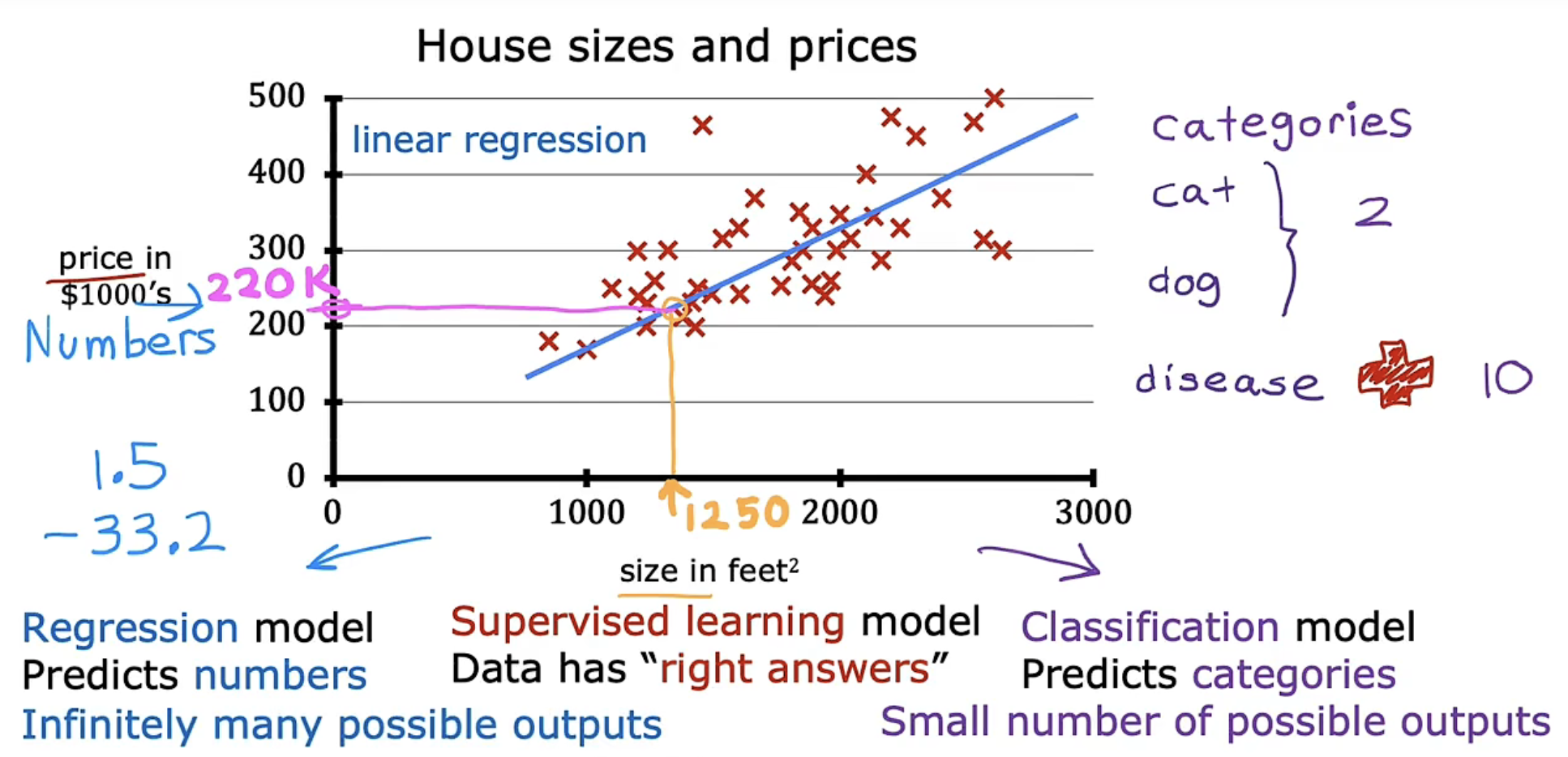
线性回归是回归的一个例子,它搭建一个线性模型,从而预测回归问题。
这里我们可以回顾一下概念
- 回归模型(Regression model)predicts numbers
Infinitely many possible outputs - 分类模型(Classification model)predicts categories
Only small number of possible outputs
4.1 机器学习中常用术语(terminology)

| 术语 | 说明 |
|---|---|
| Training Set | 训练集,即 Data used to train the model |
| x | 输入变量,即 input variable,或 feature |
| y | 输出变量,即 output variable,或 target |
| m | 训练集样本数量,即 number of training examples |
| (x, y) | 单个训练样本,即 single training example |
| \((x^{(i)}, y^{(i)})\) | 第 i 个训练样本,即 \(i^{(th)}\) training example |
| \(\widehat{y}\) | 预测标签,即 estimated output |
| parameter | 模型的参数,即 the variables you can adjust during training in order by improve the model |
4.2 函数表达
总得来说,借用机器学习的技术,我们将训练集数据结合相应的学习算法,从而生成一个函数f,以此表达输入变量与输出变量间的关系。从而,对任意给定的输入变量,我们可以借助 f 输出一个预测的输出变量(estimated)。
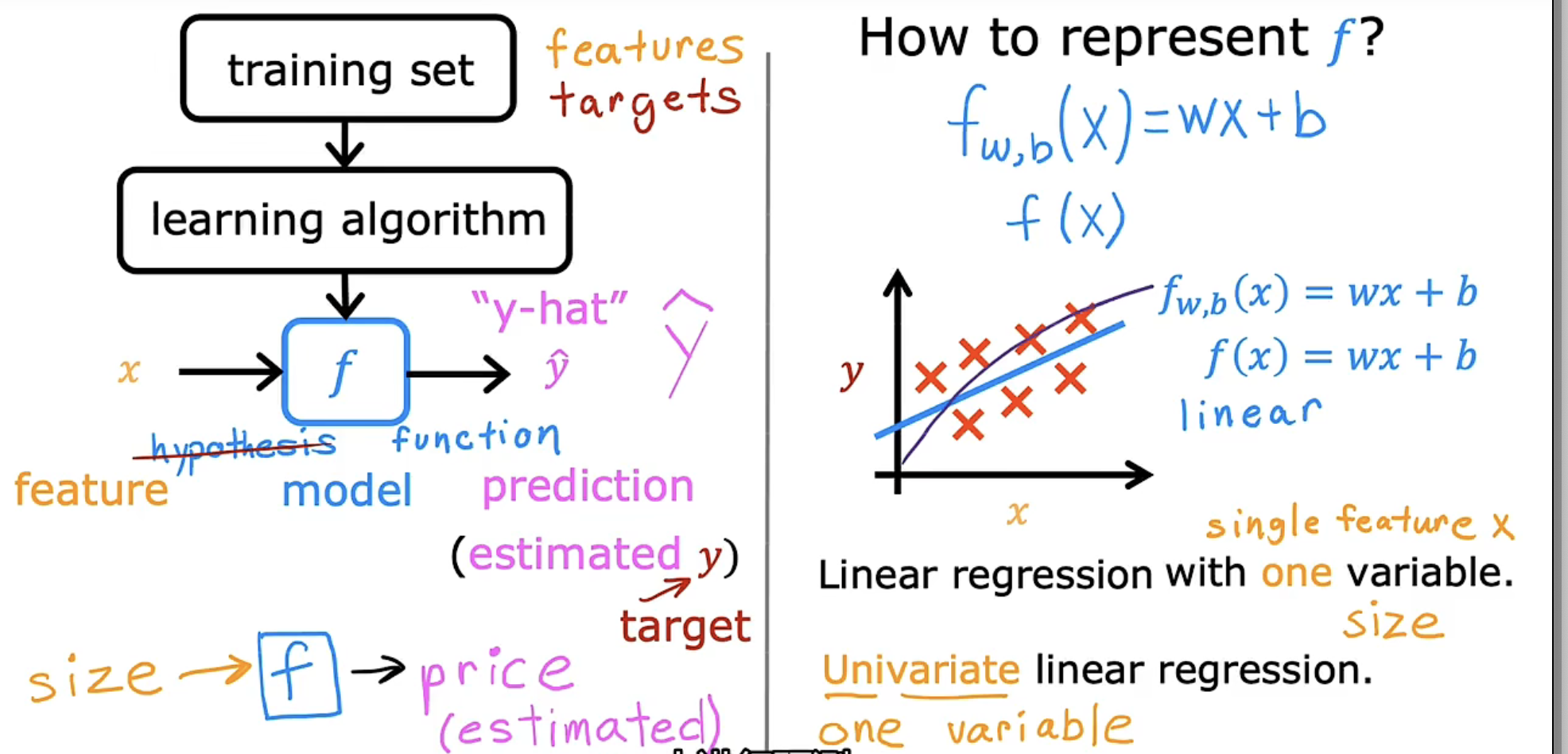
此处我们假设 f 为一个线性函数,它包括两个参数,w 代表权重(weights),b 表示偏差(bias)。
完整的表述如下:
实际使用时常简述为:
如上这种只有一个变量 x 的线性回归,称作单变量线性回归(univariate linear regression),后续我们会接触具有更多变量的线性回归,称为多变量线性回归。
4.3 代价函数(Cost function)
w 和 b 的取值可以有任意个,那究竟什么样的取值更符合我们的数据集,或者说更符合我们希望搭建的模型,我们需要相应的评价指标,即从任意取值中选取最优的取值。
以此我们可以定义线性回归的代价函数,即我们希望搭建的模型最符合我们想要的结果,预测的输出值与给定的输出值差异最小。

这里的 $ \widehat{y}^{(i)} - y^{(i)} $ 即为第 i 条样例数据对应的预测的输出值与给定的输出值的差异(error)。
为了避免代价函数取值过大,我们将每个样例数据的差异取平均处理。
这里对误差项取 $ \frac{1}{2} $ 的目的是为了方便求导,去除 $ \frac{1}{2} $ 也不影响代价函数的表达。
4.3.1 代价函数的直观理解
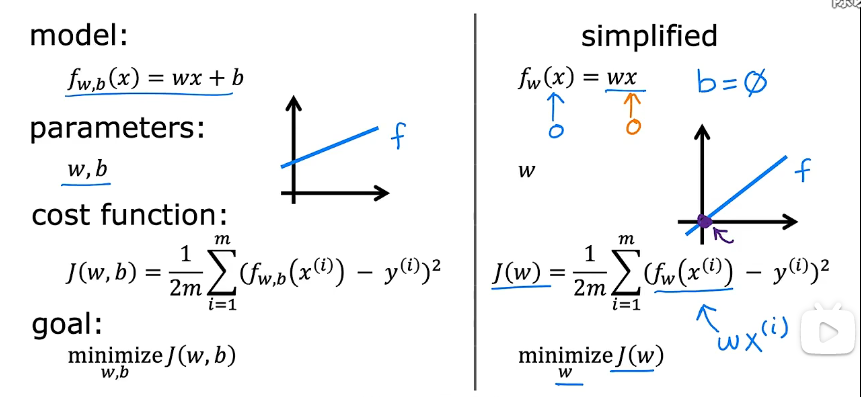
代价函数的目的是为模型找到一组合适的参数,从而使得拟合结果最符合数据表现,拟合得到的差异(error)最小。
即对于模型 $ f_{w,b}(x) = wx+b $,找到相应的参数 w、b,目标是最小化代价函数 $ J(w,b) $。
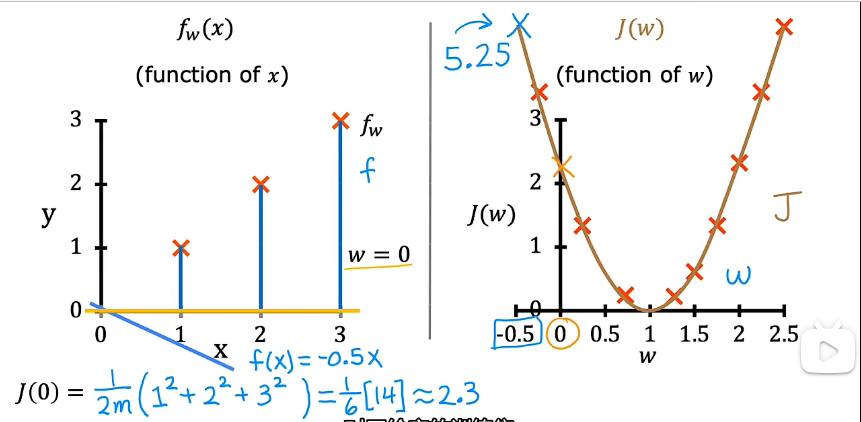
这一部分主要是详细示范了,在 b=0 的情况下,不同参数 w 的选择给代价函数带来的影响。
4.3.2 代价函数的可视化
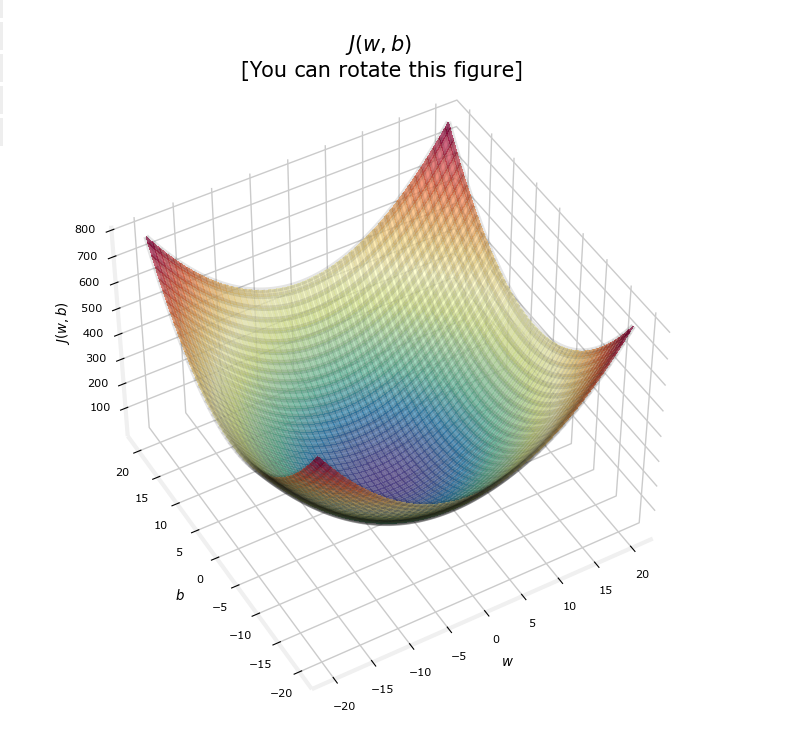
对于线性回归,代价函数是一个碗状的凸函数,这意味着存在全局最小值。
4.4 梯度下降(Gradient Descent)
梯度下降是极为常见的优化方法。
对于线性回归的代价函数 $ J(w,b) $,我们想要使得 $ J(w,b) $ 最小化。
实际上梯度下降可以推广至任意函数的优化问题上,如 $ \min_{w_1,...,w_n,b}J(w_1, w_2,..., w_n, b) $。
算法大致步骤如下:
- 初始化w,b(如设置为 0,0)
- 改变 w,b的取值,以使得 $ J(w,b) $ 减少
- 在 $ J(w,b) $ 达到或接近最小值时停止
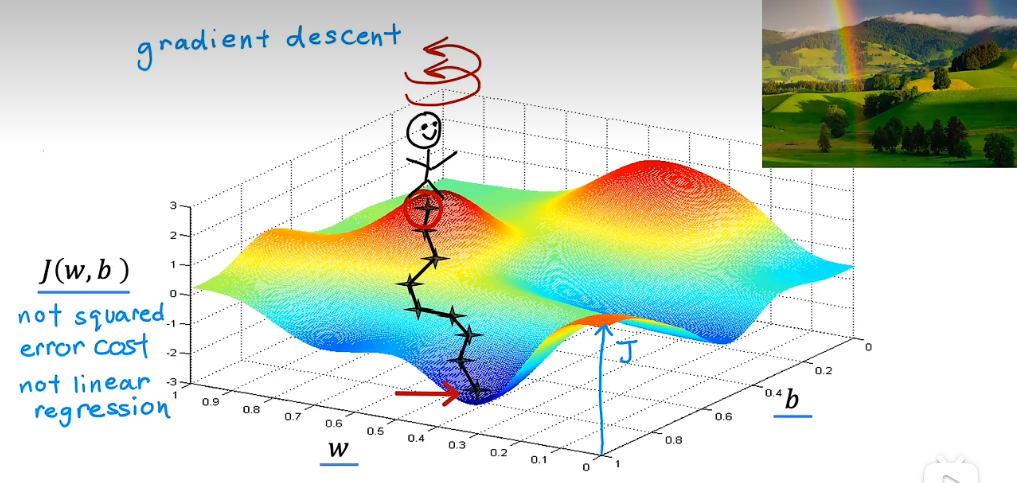
如图,可以理解成为站在山顶,每一次都朝着下山最快的方向走一小步,直至达到当前路径下的最低点。
需要注意的是,梯度下降不能保证可以达到全局最小值,有可能会陷入局部最优(local minima)。这需要依照损失函数的具体情况进行考虑。
4.4.1 梯度下降算法(Algorithm)
So far in this course, you have developed a linear model that predicts \(f_{w,b}(x^{(i)})\):
In linear regression, you utilize input training data to fit the parameters \(w\),\(b\) by minimizing a measure of the error between our predictions \(f_{w,b}(x^{(i)})\) and the actual data \(y^{(i)}\). The measure is called the \(cost\), \(J(w,b)\). In training you measure the cost over all of our training samples \(x^{(i)},y^{(i)}\)

In lecture, gradient descent was described as:
where, parameters \(w\), \(b\) are updated simultaneously.
The gradient is defined as:
Here simultaniously means that you calculate the partial derivatives for all the parameters before updating any of the parameters.
因为代价函数存在两个参数 w 与 b,因此在每一次朝着梯度最大方向移动时,这两个参数需要保持同时更新,即在进行下一次移动前更新 w 和 b。
4.4.2 学习率(learning rate)
这里引入新的概念:
- 学习率(Learning Rate)
用 $ \alpha $ 表示,可以理解成为朝着梯度最大的方向,移动时每梯度的单位距离。
$ \frac{\partial J(w,b)}{\partial w} $ 为当前梯度大小
$ \alpha \frac{\partial J(w,b)}{\partial w} $ 二者相乘,即为每次移动的实际步长。
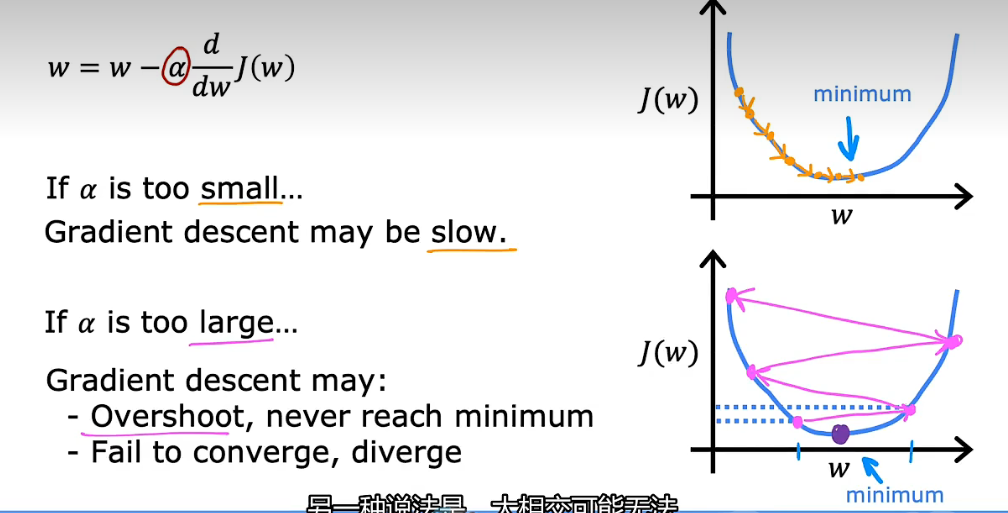
- 如果学习率太小,每次移动的步长会很小,从而代价函数收敛太慢
- 如果学习率太大,每次移动的步长太大,可能会在最小值周围反复横跳,无法收敛到最小值
当处于代价函数的局部极小值(local minimum)时,该点对应偏导数为0,从而参数 w 将不再更新。
但这也使得代价函数无法优化至全局最小值(global minimum)。
4.4.3 用于线性回归的梯度下降
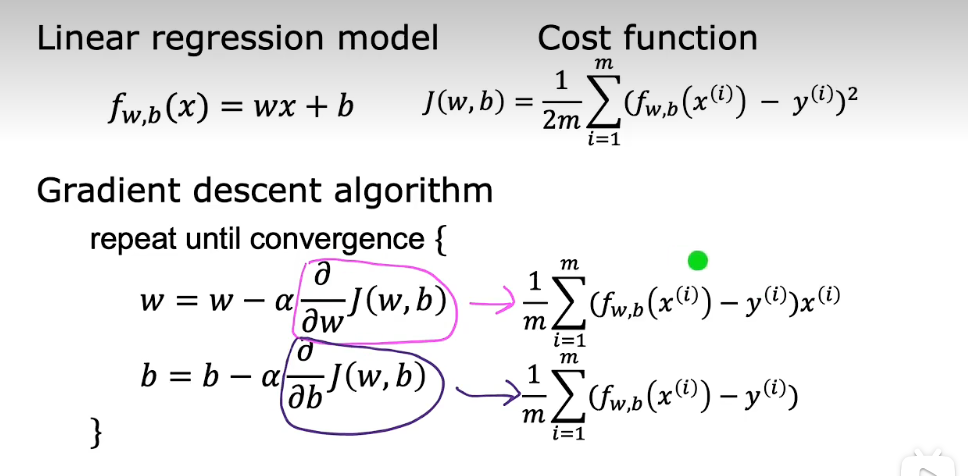
这一步主要介绍对应公式的推导过程。
接下来补充了一个新的概念:
- 批梯度下降(batch Gradient Descent)
每次更新参数时,都需要使用全部的训练数据,即为 m 条训练数据都需要参与代价函数的计算,这会使得计算量大大增加。
each step of gradient descent, uses all the training examples.
5. Optional Lab
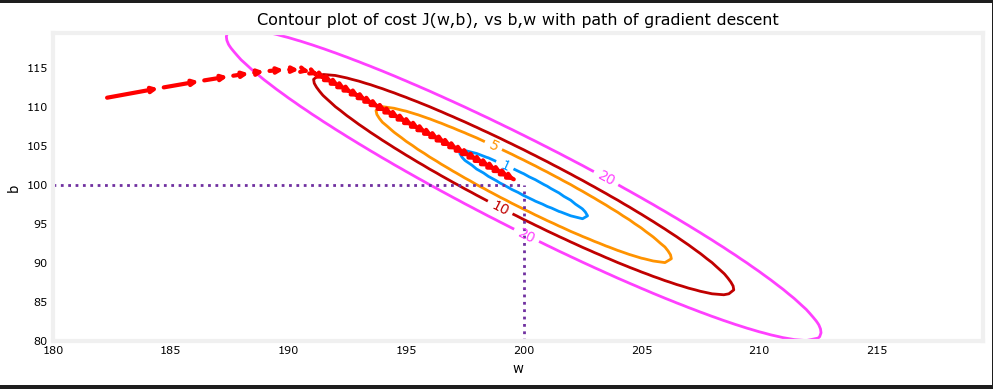
课后代码中展示了一个样例,在梯度下降过程中 w 与 b 的变化趋势。
这很符合我们的直观理解,即随着参数的更新,代价函数逐渐降低至极小值。
- Classification Supervised Regression Learning Machineclassification supervised regression learning semi-supervised cluster-guided classification semi-supervised classification adversarial supervised classification regression trees cart self-supervised classification distillation learning机器machine self-supervised bidirectional supervised learning classification learning-based fine-grained segmentation semi-supervised supervised laplacian learning clustering algorithm learning machine