description
正确的树状数组是:
void add1(int pos,int val){
while(pos<=n) c[pos]+=val,pos+=pos&-pos;
}
int ask1(int pos){
if(!pos) return 0;
int ret=0;
while(pos) ret+=c[pos],pos-=pos&-pos;
return ret mod 2;
}
一种错误的树状数组是:
void add2(int pos,int val){
while(pos) c[pos]+=val,pos-=pos&-pos;
}
int ask2(int pos){
if(!pos) return 0;
int ret=0;
while(pos<=n) ret+=c[pos],pos+=pos&-pos;
return ret mod 2;
}
注意,本题中除下标外的数值是模 2 意义下的。
给定 \(n,m\),有 \(m\) 个操作,操作有两类。
-
第一种操作,给定 \(l,r\),从 \([l,r]\) 内等概率随机出来一个点 \(x\),分别在正确的和错误的树状数组上执行 \(\text{add1(x,1)}\) 和 \(text{add2(x,1)}\)。
-
第二种操作,给定 \(l,r\),询问此时 \(\text{ask1(r)-ask1(l-1)}=\text{ask2(r)-ask2(l-1)}\) 的概率。(注意,值是模 2 意义下的,\(\text{ask}\) 的返回值只可能是 0 或 1)
solution
我们先来研究一下错误的树状数组到底干了什么。
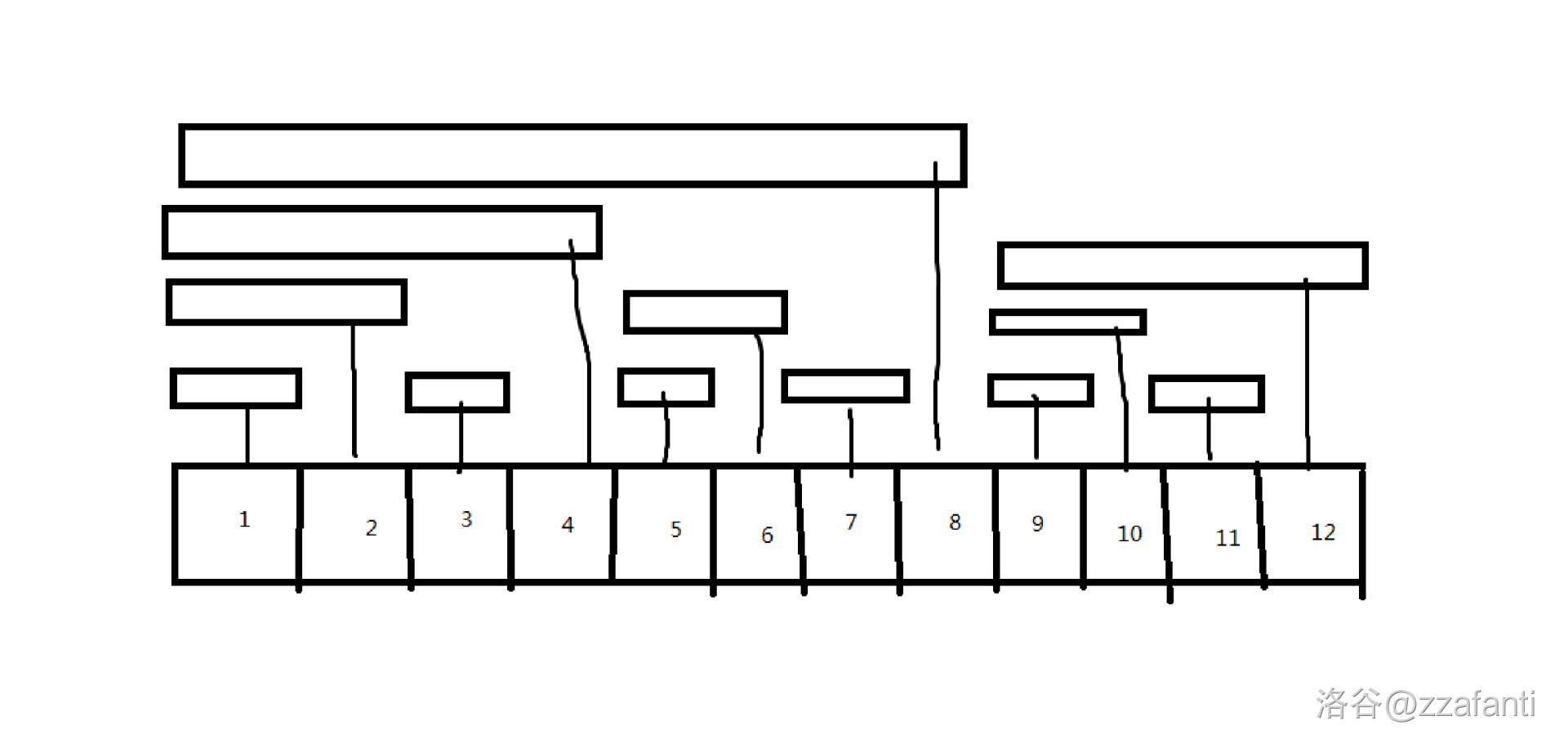
如图,我们调用 \(\text{ask2(pos)}\),它会返回覆盖了 \(pos\) 这个位置的所有节点的值的和,比如 \(\text{ask2(3)}\) 就会返回 3、4、8 号节点的值的和。
观察到 3、4、8 这样覆盖了一个位置的全部节点中一定不存在 \(x\neq y\) 使得 \(x=y-\text{lowbit(y)}\),所以每次 \(\text{add2}\) 操作至多只会对询问造成 1 的贡献,我们来观察 \(x\) 在什么情况下 \(\text{add2(x,1)}\) 能对 \(\text{ask2(pos)}\) 造成贡献。
容易观察到,只要 \(pos\ge x\) 即可。因为能贡献到 \(P\) 的 \(x\) 需 \(\in [P,P+\text{lowbit(P)}-1]\),而所有覆盖 \(pos\) 的节点能被贡献的区间的并就比较容易看出来是 \([pos,n]\) 了。
综上,我们得出结论:
对正整数 \(pos\),错误的树状数组执行 \(\text{ask2(pos)}\) 的到的结果是 \([pos,n]\) 的和;特别地,当 \(pos=0\) 时,\(\text{ask2(pos)}=0\)。
这是个非常可爱的结论,问题瞬间看上去容易了许多。
先不考虑 \(l=1\),也就是,正确的树状数组求出的是 \([l,r]\) 的和,而错误的树状数组求出的是 \([l-1,r-1]\) 的和。
如果 \(l=1\),正确的树状数组求出了 \([l,r]\) 的和,而错误的求出了 \([r,n]\) 的和。
对两种情况分别 dp 一下,就得到了 \(O(m^2+m\log V)\) 的算法。(\(\log V\) 是求逆元,实际实现成 \(O(m^2\log V)\) 也可以拿满这档部分分)
具体地,我们先把所有询问的区间左端点减 1,这么处理后,对于询问 \([l,r]\),\(f_{i,0}\) 表示考虑前 \(i\) 个类型 1 的操作,正确和错误的树状数组得到的结果相同的概率,\(f_{i,1}\) 表示不相同的概率,设第 \(i\) 个类型 1 的操作的操作区间是 \([L,R]\),则有转移:
-
\(f_{i,0}=\dfrac{1}{R-L+1}(f_{i,1}([L\leq l\leq R]+[L\leq r\leq R])+f_{i,0}(R-L+1-[L\leq l\leq R]-[L\leq r\leq R]))\),\(l\neq 0\)
-
\(f_{i,1}=\dfrac{1}{R-L+1}(f_{i,0}([L\leq l\leq R]+[L\leq r\leq R])+f_{i,1}(R-L+1-[L\leq l\leq R]-[L\leq r\leq R]))\),\(l\neq 0\)
-
\(f_{i,0}=\dfrac{1}{R-L+1}(f_{i,1}(R-L+1-[L\leq r\leq R])+f_{i,0}[L\leq r\leq R])\)
-
\(f_{i,1}=\dfrac{1}{R-L+1}(f_{i,0}(R-L+1-[L\leq r\leq R])+f_{i,1}[L\leq r\leq R])\)
有 50 分。
来做正解!
先考虑询问都在类型 1 后面怎么做。
我们对每个类型 1 的操作用三棵分别维护两种 \(l\) 不等于 0 和一种 \(l\) 等于 0 的矩阵。(\(l\neq 0\) 时如果询问的左右端点都被包含了常数就是 2,否则是 1)
如果 \(l\neq 0\),对于每个询问,我们要知道:
-
包含左端点,但不包含右端点的类型 1 的矩阵乘积。
-
不包含左端点,但包含右端点的类型 1 的矩阵乘积。
-
既包含左端点,又包含右端点的类型 1 的矩阵乘积。
前两种的矩阵相同,常数都是 1,最后一种常数是 2。
如果 \(l=0\),我们要知道所有包含右端点的类型 1 的转移矩阵的乘积,还要知道所有不包含右端点的类型 1 的转移矩阵的乘积(此时矩阵是交换了上下行的 \(2\times 2\) 的单位矩阵的乘积)。
离线排序维护即可。
不保证所有询问在类型 1 后面就套个 CDQ 分治。
时间复杂度 \(O(m\log m\log n)\)
注意常数!
建议把矩阵直接用 \(a,b,c,d\) 存,相较数组效率有极显著的提高。
code
#include<bits/stdc++.h>
using namespace std;
using E=long long;
constexpr E mod=998244353;
E ksm(E a,E b){
E ret=1;
while(b){
if(b&1) ret=ret*a%mod;
a=a*a%mod;
b>>=1;
}
return ret;
}
struct fenwick{
vector<int> c;
fenwick(int sz=0){
c=vector<int>(sz+1,0);
}
void add(int pos,int val){
if(!(pos&&pos<c.size())) return ;
while(pos<c.size()) c[pos]+=val,pos+=pos&-pos;
}
int ask(int pos){
if(!pos) return 0;
int ret=0;
while(pos) ret+=c[pos],pos-=pos&-pos;
return ret;
}
};
struct matrix{
E a,b,c,d;
matrix(int n=0,int m=0,int v=0){
a=b=c=d=0;
if(v) a=d=v;
}
friend matrix operator * (const matrix &x,const matrix &y){
matrix z(2,2);
z.a=x.b*y.c%mod+x.a*y.a%mod;
if(z.a>=mod) z.a-=mod;
z.b=x.b*y.d%mod+x.a*y.b%mod;
if(z.b>=mod) z.b-=mod;
z.c=x.d*y.c%mod+x.c*y.a%mod;
if(z.c>=mod) z.c-=mod;
z.d=x.d*y.d%mod+x.c*y.b%mod;
if(z.d>=mod) z.d-=mod;
return z;
}
};
struct segment{
vector<matrix> sum;
segment(int sz){
sum=vector<matrix>(sz*4+1,matrix(2,2,1));
}
void reset(int u,int l,int r,int pos){
if(l==r){
sum[u]=matrix(2,2,1);
return ;
}
int mid=(l+r)>>1;
if(pos<=mid) reset(u<<1,l,mid,pos);
else reset(u<<1|1,mid+1,r,pos);
sum[u]=sum[u<<1]*sum[u<<1|1];
}
void add(int u,int l,int r,int pos,const matrix &val){
if(l==r){
sum[u]=sum[u]*val;
return ;
}
int mid=(l+r)>>1;
if(pos<=mid) add(u<<1,l,mid,pos,val);
else add(u<<1|1,mid+1,r,pos,val);
sum[u]=sum[u<<1]*sum[u<<1|1];
}
matrix query(int u,int l,int r,int L,int R){
if(L<=l&&r<=R) return sum[u];
int mid=(l+r)>>1;
if(L<=mid&&mid<R) return query(u<<1,l,mid,L,R)*query(u<<1|1,mid+1,r,L,R);
if(mid<R) return query(u<<1|1,mid+1,r,L,R);
return query(u<<1,l,mid,L,R);
}
};
struct querys{
int op,l,r,idx;
};
int n,m;
vector<matrix> res1,res2,res3;
vector<querys> Q;
segment seg1(0),seg2(0),seg3(0);
fenwick tr;
void solve(int ll,int rr){
if(ll==rr){
return ;
}
int mid=(ll+rr)>>1;
solve(ll,mid);
vector<querys> pt;
for(int i=ll; i<=rr; i++){
if((i<=mid)^(Q[i].op==2)) pt.emplace_back(Q[i]);
}
sort(pt.begin(),pt.end(),
[&](const querys &x,const querys &y){
return x.r==y.r?(x.op<y.op):x.r>y.r;
});
vector<int> stk;
for(auto p:pt){
int i=p.idx,l=p.l,r=p.r;
if(p.op==1){
stk.emplace_back(l);
E P=ksm(r-l+1,mod-2);
matrix trans(2,2);
trans.a=trans.d=(r-l)*P%mod;
trans.b=trans.c=P;
seg1.add(1,1,n,l,trans);
trans.a=trans.d=P;
trans.b=trans.c=(r-l)*P%mod;
seg3.add(1,1,n,l,trans);
if(l==r) continue;
trans.a=trans.d=(r-l-1)*P%mod;
trans.c=trans.b=2*P%mod;
seg2.add(1,1,n,l,trans);
}
else{
if(l) res2[i]=res2[i]*seg1.query(1,1,n,l+1,r);
else res2[i]=res2[i]*seg3.query(1,1,n,l+1,r);
if(l) res3[i]=res3[i]*seg2.query(1,1,n,1,l);
}
}
sort(stk.begin(),stk.end());
stk.erase(unique(stk.begin(),stk.end()),stk.end());
for(auto p:stk){
seg1.reset(1,1,n,p);
seg2.reset(1,1,n,p);
seg3.reset(1,1,n,p);
}
sort(pt.begin(),pt.end(),
[&](const querys &x,const querys &y){
return x.l==y.l?(x.op<y.op):x.l<y.l;
});
stk.clear();
for(auto p:pt){
int l=p.l,r=p.r,i=p.idx;
if(p.op==1){
E P=ksm(r-l+1,mod-2);
stk.emplace_back(r);
matrix trans(2,2);
trans.a=trans.d=(r-l)*P%mod;
trans.c=trans.b=P;
seg1.add(1,1,n,r,trans);
}
else{
if(!l) continue;
res1[i]=res1[i]*seg1.query(1,1,n,l,r-1);
}
}
for(auto p:stk){
seg1.reset(1,1,n,p);
}
solve(mid+1,rr);
};
int main(){
#ifdef zzafanti
freopen("in.in","r",stdin);
#endif // zzafanti
cin.tie(nullptr),cout.tie(nullptr)->sync_with_stdio(false);
cin>>n>>m;
Q=vector<querys>(m+1);
res1=res2=res3=vector<matrix>(m+1);
seg3=seg1=seg2=segment(n);
tr=fenwick(n);
int cc=0;
vector<int> tag(m+1);
for(int i=1; i<=m; i++){
cin>>Q[i].op>>Q[i].l>>Q[i].r;
Q[i].idx=i;
if(Q[i].op==2){
Q[i].l--;
if(!Q[i].l) tag[i]=cc-tr.ask(Q[i].r);
res1[i]=res2[i]=res3[i]=matrix(2,2,1);
}else cc++,tr.add(Q[i].l,1),tr.add(Q[i].r+1,-1);
}
solve(1,m);
for(int i=1; i<=m; i++){
if(Q[i].op==1) continue;
matrix init(2,2,0);
init.a=1,init.b=0;
init=init*res1[i]*res2[i]*res3[i];
if(Q[i].l==0&&tag[i]%2==1) cout<<init.b<<'\n';
else cout<<init.a<<'\n';
}
return 0;
}