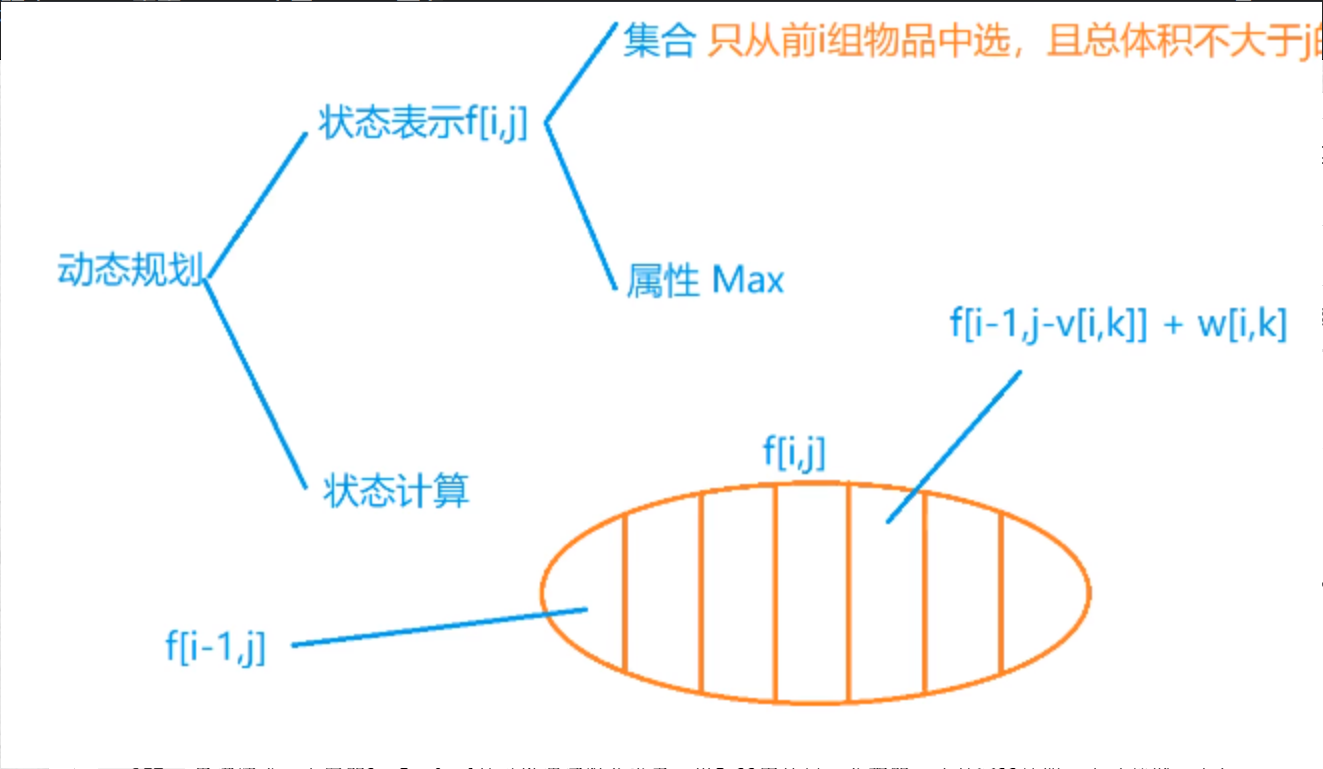
（1） 01背包

01背包
二维

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 1010;

int n, m;
int v[N], w[N];//v 保存体积，w 保存价值
int f[N][N];//保存所有集合最值状态

int main()
{
    cin >> n >> m;

    for (int i = 1; i <= n; i ++ )
        cin >> v[i] >> w[i];

    for(int i = 0; i <= m; i++)//初始化，前 0 中物品中选择
    {
        f[0][i] = 0;
    }

    for (int i = 1; i <= n; i ++ )
    {
        for (int j = 1; j <= m; j ++)
        {
            if(v[i] <= j)//能放入第 i 件物品的情况下，求f[i][j]
                f[i][j] = max(f[i - 1][j], f[i - 1][j - v[i]] + w[i]);
            else//不能放入第 i 件物品的情况下，求f[i][j]
                f[i][j] = f[i - 1][j];
        }

    }
    cout << f[n][m] << endl;//f[n][m] 就是答案

    return 0;
}

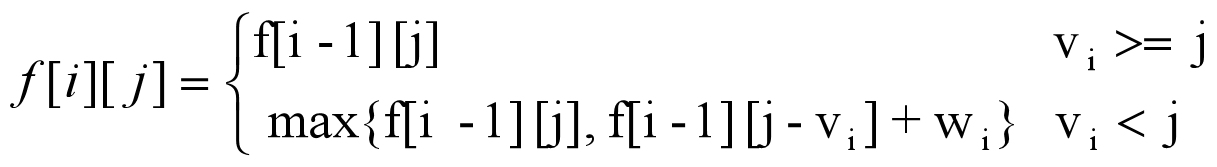
从计算公式可以看出，f[i][j] 是由 f[i - 1][j -vi] 和 wi计算出来的。也就是f[i][j]的值是可以从前面已经计算出的 f 值求出来。如果我们能确定 f[i][j] 的一部分初始值，就能通过该公式，一步步计算得出 f[N][V]，也就是我们要找的答案。
一维优化

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
int n,m;
const int N=1010;
int dp[N],w[N],v[N];

int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++) cin>>v[i]>>w[i];

    for(int i=1;i<=n;i++)
    {
        for(int j=m;j>=v[i];j--)
            dp[j]=max(dp[j],dp[j-v[i]]+w[i]);
    }
    cout<<dp[m];
}

为什么逆序
若j从小到大，f[j-v[i]]中，由于j-v[i]小于j，f[j-v[i]]已经在i这层循环被计算了，而我们想要的f[j-v[i]]应该是i-1层循环里面的，所以j从大到小的话保证此时的f[j-v[i]]还未被计算，也就是第i-1层的数据

举例

4 5
1 2
2 4
3 4
4 5

最大方案是选2和3

如果从前往后遍历，遍历到dp[3]时，dp[3]！＝4，而是在前面被更新为6，所以要从后往前遍历，
也就是第i-1层的数据没有被”污染“

(2) 完全背包

完全背包
没优化前代码

#include<iostream>
using namespace std;
const int N = 1010;
int f[N][N];
int v[N],w[N];
int main()
{
    int n,m;
    cin>>n>>m;
    for(int i = 1 ; i <= n ;i ++)
    {
        cin>>v[i]>>w[i];
    }

    for(int i = 1 ; i<=n ;i++)
    for(int j = 0 ; j<=m ;j++)
    {
        for(int k = 0 ; k*v[i]<=j ; k++)
            f[i][j] = max(f[i][j],f[i-1][j-k*v[i]]+k*w[i]);
    }

    cout<<f[n][m]<<endl;
}

优化思路
更新次序的内部关系：

f[i , j ] = max( f[i-1,j] , f[i-1,j-v]+w ,  f[i-1,j-2*v]+2*w , f[i-1,j-3*v]+3*w , .....)
f[i , j-v]= max(            f[i-1,j-v]   ,  f[i-1,j-2*v] + w , f[i-1,j-3*v]+2*w , .....)
由上两式，可得出如下递推关系： 
			     f[i][j]=max(f[i,j-v]+w , f[i-1][j]) 

有了上面的关系，那么其实k循环可以不要了(喜新厌旧hh)，核心代码优化成这样：

for(int i = 1 ; i <=n ;i++)
for(int j = 0 ; j <=m ;j++)
{
    f[i][j] = f[i-1][j];
    if(j-v[i]>=0)
        f[i][j]=max(f[i][j],f[i][j-v[i]]+w[i]);
}

这个代码和01背包的非优化写法很像!!!对比一下，下面是01背包的核心代码

for(int i = 1 ; i <= n ; i++)
for(int j = 0 ; j <= m ; j ++)
{
    f[i][j] = f[i-1][j];
    if(j-v[i]>=0)
        f[i][j] = max(f[i][j],f[i-1][j-v[i]]+w[i]);
}

两个代码其实只有一句不同（注意下标）

f[i][j] = max(f[i][j],f[i-1][j-v[i]]+w[i]);//01背包

f[i][j] = max(f[i][j],f[i][j-v[i]]+w[i]);//完全背包问题

因为和01背包代码很相像，我们很容易想到进一步优化。核心代码可以改成下面这样

 for(int i = 1 ; i<=n ;i++)
    for(int j = v[i] ; j<=m ;j++)//注意了，这里的j是从小到大枚举，和01背包不一样
    {
            f[j] = max(f[j],f[j-v[i]]+w[i]);
    }

优化后代码如下

#include<iostream>
using namespace std;
const int N = 1010;
int f[N];
int v[N],w[N];
int main()
{
    int n,m;
    cin>>n>>m;
    for(int i = 1 ; i <= n ;i ++)
    {
        cin>>v[i]>>w[i];
    }

    for(int i = 1 ; i<=n ;i++)
    for(int j = v[i] ; j<=m ;j++)
    {
            f[j] = max(f[j],f[j-v[i]]+w[i]);
    }
    cout<<f[m]<<endl;
}

(3) 多重背包

1> 未优化

多重背包1
状态转移方程

f[i][j] = max(f[i - 1][j],f[i - 1][j - k * v[i]] + w[i] * k);

和完全背包差不错

#include <iostream>
#include <algorithm>
using namespace std;
const int N = 110;
int n,m;
int v[N],w[N],s[N];
int f[N][N];
int main(){
    cin>>n>>m;
    for(int i = 1;i <= n;i ++) cin>>v[i]>>w[i]>>s[i];
    for(int i = 1;i <= n;i ++){
        for(int j = 0;j <= m;j ++){
            for(int k = 0;k <= s[i];k ++){
                if(j >= v[i] * k) f[i][j] = max(f[i][j],f[i - 1][j - k * v[i]] + w[i] * k);
            }
        }
    }
    cout<<f[n][m]<<endl;
    return 0;
}

2>按01背包的扩展来写

多重背包是选一个，两个...到s个，01背包是选和不选

(按01背包写)

for(int i=0;i<n;i++)
    {
        int v,w,s;
        cin>>v>>w>>s;
        for(int j=m;j>=0;j--)
            for(int k=1;k<=s;k++)
            if(j>=k*v)
            f[j]=max(f[j],f[j-k*v]+k*w);
    }

可以把多重背包中选几个看作为01背包的第i项目选不选
例如
1 2 3
2 4 1
3 4 3
4 5 2
就可以看作为第一个物品选一个，选两个，选三个。三种方案，体积就对应为k*v，价值就是k*w,此时就可当作01背包（后面三个依然如此）

(按正常三重循环)

for(int i = 1;i <= n;i ++){
        for(int j = 0;j <= m;j ++){
            for(int k = 0;k <= s[i];k ++){
                if(j >= v[i] * k) f[i][j] = max(f[i][j],f[i - 1][j - k * v[i]] + w[i] * k);
            }
        }
    }

#include<iostream>
#include<cstring>
#include<cstring>

using namespace std;

const int N=110;
int n,m;
int f[N];

int main()
{
    cin>>n>>m;
    for(int i=0;i<n;i++)
    {
        int v,w,s;
        cin>>v>>w>>s;
        for(int j=m;j>=0;j--)
            for(int k=1;k<=s;k++)
            if(j>=k*v)
            f[j]=max(f[j],f[j-k*v]+k*w);
    }
    cout<<f[m];
}

3> 优化版本

#include<iostream>
using namespace std;
const int N=25000;
int f[N],v[N],w[N];
int n,m;
int main()
{
    cin>>n>>m;
    int cnt=0;
    for(int i=1;i<=n;i++)
    {
        int a,b,s;//体积，价值，数量
        cin>>a>>b>>s;
        int k=1;
        while(k<=s)
        {
            cnt++;
            v[cnt]=a*k;
            w[cnt]=b*k;
            s-=k;
            k*=2;
        }
        if(s>0)
        {
            cnt++;
            v[cnt]=s*a;
            w[cnt]=s*b;
        }
    }
    
    n=cnt;
    
    for(int i=1;i<=n;i++)
    {
        for(int j=m;j>=v[i];j--)
        {
            f[j]=max(f[j],f[j-v[i]]+w[i]);
        }
    }
    cout<<f[m];
}

优化多重背包的优化
首先，我们不能用完全背包的优化思路来优化这个问题，因为每组的物品的个数都不一样，是不能像之前一样推导不优化递推关系的。（因为多重背包数量是有限的）
我们列举一下更新次序的内部关系：

f[i , j ] = max( f[i-1,j] ,   f[i-1,j-v]+w ,    f[i-1,j-2v]+2*w , f[i-1,j-3v]+3*w , .....,f[i-1,j-Sv]+S*w)
f[i , j-v]= max(              f[i-1,j-v] ,      f[i-1,j-2v] + w , f[i-1,j-3v]+2*w , .....,f[i-1,j-Sv]+(S-1)*w,f[i-1,j-(S+1)v]+S*w)
由上两式，可得出如下递推关系：
f[ i ][ j ] = max(f[i,j-v]+w , f[i-1][j])

接下来，我介绍一个二进制优化的方法，假设有一组商品，一共有11个。我们知道，十进制数字 11 可以这样表示

11=1011(B)=0111(B)+(11−0111(B))=0111(B)+0100(B)

正常背包的思路下，我们要求出含这组商品的最优解，我们要枚举12次（枚举装0，1，2....12个）。

现在，如果我们把这11个商品分别打包成含商品个数为1个，2个，4个，4个（分别对应0001,0010,0100,0100）的四个”新的商品 “, 将问题转化为01背包问题，对于每个商品，我们都只枚举一次，那么我们只需要枚举四次 ，就可以找出这含组商品的最优解。 这样就大大减少了枚举次数。

这种优化对于大数尤其明显，例如有1024个商品，在正常情况下要枚举1025次 ， 二进制思想下转化成01背包只需要枚举10次。

优化的合理性的证明
先讲结论：上面的1，2，4，4是可以通过组合来表示出0~11中任何一个数的，还是拿11证明一下（举例一下）：

首先，11可以这样分成两个二进制数的组合：
11=1011(B)=0111(B)+(11−0111(B))=0111(B)+0100(B)
其中0111通过枚举这三个1的取或不取（也就是对0001(B)，0010(B)，0100(B)的组合），可以表示十进制数0~7( 刚好对应了 1，2，4 可以组合出 0~7 ) , 0~7的枚举再组合上0100(B)( 即 十进制的 4 ) ，可以表示十进制数 0~11。其它情况也可以这样证明。这也是为什么，这个完全背包问题可以等效转化为01背包问题，有木有觉得很奇妙
怎么合理划分一个十进制数?
上面我把11划分为

  	     11=1011(B)=0111(B)+(11−0111(B))=0111(B)+0100(B)

是因为 0111(B)刚好是小于11的最大的尾部全为1的二进制 ( 按照上面的证明，这样的划分没毛病 ) , 然后那个尾部全为1的数又可以 分解为 0000....1 , 0000....10 , 0000....100 等等。

(4) 分组背包

分组背包

	#include<bits/stdc++.h>
	using namespace std;
	const int N=110;
	int f[N][N];  //只从前i组物品中选，当前体积小于等于j的最大值
	int v[N][N],w[N][N],s[N];   //v为体积，w为价值，s代表第i组物品的个数
	int n,m,k;
	
	int main(){
    cin>>n>>m;
    for(int i=1;i<=n;i++){
        cin>>s[i];
        for(int j=0;j<s[i];j++){
            cin>>v[i][j]>>w[i][j];  //读入
        }
    }
    for(int i=1;i<=n;i++){
        for(int j=0;j<=m;j++){
            f[i][j]=f[i-1][j];  //不选
            for(int k=0;k<s[i];k++){
                if(j>=v[i][k])     f[i][j]=max(f[i][j],f[i-1][j-v[i][k]]+w[i][k]);  
            }
        }
    }
    cout<<f[n][m]<<endl;
	}

因为数据只用到i-1行的数据，所以要效仿01背包逆序枚举

	#include<bits/stdc++.h>
	using namespace std;
	
	const int N=110;
	int f[N];
	int v[N][N],w[N][N],s[N];
	int n,m,k;
	
	int main(){
    cin>>n>>m;
    for(int i=0;i<n;i++){
        cin>>s[i];
        for(int j=0;j<s[i];j++){
            cin>>v[i][j]>>w[i][j];
        }
    }
	
    for(int i=0;i<n;i++){
        for(int j=m;j>=0;j--){
            for(int k=0;k<s[i];k++){    //for(int k=s[i];k>=1;k--)也可以
                if(j>=v[i][k])     f[j]=max(f[j],f[j-v[i][k]]+w[i][k]);  
            }
        }
    }
    cout<<f[m]<<endl;
	}

本栏目推荐文章
• 解决 DELPHI 中执行外部命令出现屏幕一闪的问题的方法
• 从C++CLI工程的依赖库引用问题看.Net加载程序集机制
• Maven常见问题与原理技巧
• Hive常见问题
• VIM/NeoVIM：解决LuaSnip下Tab按键跳转冲突问题
• 【Leetcode 2474. 购买量严格增加的客户】MySQL用户变量编程解决严格递增连续子序列问题
• 【LeetCode 2494. 合并在同一个大厅重叠的活动】MySQL用户变量编程解决区间合并问题
• Spark版本不兼容导致Standalone集群无法连接问题
• 2d物理引擎学习 - 基于约束的公式解决接触稳定性问题
• 深拷贝和浅拷贝的问题 [补档-2022-10-22]

背包 问题背包 问题 背包 动态 问题 背包acwing问题 算法 背包 问题 背包acwing问题ii 背包 模板 问题 背包continued问题to 背包 随想录 子集 问题 问题 背包 结构 限界 分支 背包 问题