T1 无聊的草稿 GMOJ 1752
Description
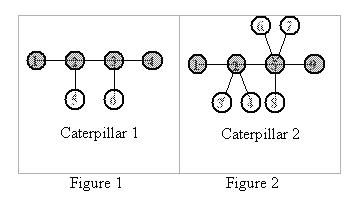
图中有N个点,每两点间只有唯一的路径,对于这样一个给定的图,最大的“毛毛虫”会有多大。毛毛虫包含一条主链,毛毛虫中的节点,要不在主链上,要么和主链上某节点相邻,如下图所示有两只合法的毛毛虫,点数越多,毛毛虫越大。
Input
输入文件第一行两个整数N,M(N≤1000000)
接下来M行,每行两个整数a, b(a, b≤N)
你可以假定没有一对相同的(a, b)会出现一次以上。Output
一个整数ans,表示最大的毛毛虫的大小。
Sample Input
5 4 1 2 1 3 4 1 5 1Sample Output
5Data Constraint
Hint
【数据规模】
1. 对于20%的数据,N≤200
2. 对于40%的数据,N≤5000
3. 对于100%的数据,N≤10^6
比赛时一眼直径。可惜我不会……
下次一定把“树上问题”给看完。
然后我就在比赛时想到一个方法(好似就是用树形dp求直径)
下面定义 \(\text{child}\) 为儿子数量
定义 \(f[i]\) 表示以 \(i\) 为毛毛虫端点的最大毛毛虫大小,可以分为两种情况:
-
自己是毛毛虫起点
\[f[i]=\text{child}+1 \] -
自己继承儿子的毛毛虫
\[f[i]=\max(child-1+1+f[j],f[i]) \]意思表示当前的毛毛虫大小为儿子的数量,减去继承的那个儿子的1,加上自己的1,加上继承那个儿子的子树大小。
然后就快乐的对拍啦!
然后还好我对拍了,我就发现上面的做法并不可行。
如果出现了:
我们会发现,最好的毛毛虫是整棵树,但是在这里,我们计算出来的只有是1的两个子树中的毛毛虫大小,即5。
怎么解决呢?所以我定义了 \(g[i]\) 表示以 \(i\) 为承接点(例如上面的 \(1\))的最大毛毛虫大小。
这样理解可能会很困难,所以我可以这么理解:
- \(f[i]\) : \(i\) 为毛毛虫中一个节点,且 \(i\) 的父亲(根节点除外)也为毛毛虫的最大毛毛虫大小
- \(g[i]\) : \(i\) 为毛毛虫中一个节点,但 \(i\) 的父亲(根节点除外)不为毛毛虫的最大毛毛虫大小
附上 \(g\) 的计算方式:
可能很难理解,我附上说明:意思是当前的毛毛虫大小为最大子树和次大子树大小之和,加上包括父亲(根节点除外)的周围节点数量,再减去两个子节点,再加上自己。
总结:
树上问题完全没有看完,遇到只能完蛋。
#include <cstdio>
#define ll long long
int n, m;
int ans;
int f[1000010];
int g[1000010];
int head[2000010];
int nxt[2000010];
int to[2000010], cnt;
void addEdge(int u, int v) {
cnt++;
to[cnt] = v;
nxt[cnt] = head[u];
head[u] = cnt;
}
inline int max(int x, int y) {
return x>y?x:y;
}
void dfs(int u, int fa) {
bool isFa = fa;
int child = 0;
for(int i = head[u]; i; i = nxt[i]) {
int v = to[i];
if(v != fa) child++;
}
// 方案1:把自己看作新链
f[u] = child + 1;
int mx1 = 0, mx2 = 0;
for(int i = head[u]; i; i = nxt[i]) {
// 方案2:选择儿子的一条新链
int v = to[i];
if(v == fa) continue;
dfs(v, u);
f[u] = max(f[u], child + f[v]);
if(f[v] > mx1) {
mx2 = mx1;
mx1 = f[v];
} else if(f[v] > mx2) {
mx2 = f[v];
}
}
// 方案3:选择两个大儿子配对
if(mx1 && mx2) {
// 自己 两个大儿子 包括父亲在内的相邻节点减去两个大儿子
g[u] = 1 + mx1 + mx2 + (child + isFa) - 2;
}
}
int main() {
scanf("%d %d", &n, &m);
for(int i = 1; i <= m; i++) {
ll u, v;
scanf("%lld %lld", &u, &v);
addEdge(u, v);
addEdge(v, u);
}
dfs(1,0);
for(int i = 1; i <= n; i++) {
ans = max(ans, max(f[i], g[i]));
// printf("g[%lld]=%lld\n",i,g[i]);
}
printf("%d", ans);
}
T2 资源勘探 GMOJ 1282
Description
教主要带领一群Orzer到一个雄奇地方勘察资源。
这个地方可以用一个n×m的矩阵A[i, j]来描述,而教主所在的位置则是位于矩阵的第1行第1列。
矩阵的每一个元素A[i, j]均为一个不超过n×m的正整数,描述了位于这个位置资源的类型为第A[i, j]类。教主准备选择一个子矩阵作为勘察的范围,矩阵的左上角即为教主所在的(1, 1)。若某类资源k在教主勘察的范围内恰好出现一次。或者说若教主选择了(x, y)即第x行第y列作为子矩阵的右下角,那么在这个子矩阵中只有一个A[i, j](1≤i≤x,1≤j≤y)满足A[i, j]=k,那么第k类资源则被教主认为是稀有资源。
现在问题是,对于所有的(x, y),询问若(x, y)作为子矩阵的右下角,会有多少类不同的资源被教主认为是稀有资源。Input
输入的第一行包括两个正整数n和m,接下来n行,每行m个数字,描述了A[i, j]这个矩阵。
Output
为了照顾Vijos脑残的输出问题,设B[i, j]表示仅包含前i行与前j列的子矩阵有多少个数字恰好出现一次,那么你所要输出所有B[i, j]之和mod 19900907。
Sample Input
2 3 1 2 3 3 1 2Sample Output
10Data Constraint
Hint
【样例说明】
对于右下角为(1,1)的子矩阵,仅包含数字1,所以答案为1。
对于右下角为(1,2)的子矩阵,数字1、2各出现一次,所以答案为2。
对于右下角为(1,3)的子矩阵,数字1、2、3各出现一次,所以答案为3。
对于右下角为(2,1)的子矩阵,数字1、3各出现一次,所以答案为2。
对于右下角为(2,2)的子矩阵,数字2、3各出现一次,但是数字1出现了两次,所以数字1不统计入答案,答案为2。
对于右下角为(2,3)的子矩阵,数字1、2、3均出现了两次,所以答案为0。
【数据说明】
对于10%的数据,有N,M≤10;
对于20%的数据,有N,M≤20;
对于40%的数据,有N,M≤150;
对于50%的数据,A[I, J]≤1000;
对于70%的数据,有N,M≤800;
对于100%的数据,有N,M≤1100,A[I, J] ≤N×M。
比赛时不会,现在会了也很蒙?
维护 \(b[j]\) 为第j列对答案的贡献。
那么贡献分为几类:
- 第一次出现,对答案贡献为 \(1\)
- 第二次出现,对答案贡献为 \(-1\)
- 第n>2次出现,对答案贡献为 \(0\)
我们分别考虑这三种情况,然后计算答案就行了。
总结:这种分别计算各元素对答案的贡献的思想不了解,导致本可以想到上面的(但是能不能打出来是另一码事)
#include <cstdio>
#define ll long long
#define P 19900907
ll a[1110][1110]; // QWQ
ll b[1110]; // b 储存某一列的贡献
ll v1[1110*1110]; // v1 储存最左出现的列数
ll v2[1110*1110]; // v2 储存第二左出现
ll n, m;
ll cnt, ans;
int main() {
scanf("%lld %lld", &n, &m);
for(ll i = 1; i <= n; i++) {
for(ll j = 1; j <= m; j++) {
scanf("%lld", &a[i][j]);
}
}
for(ll i = 1; i <= n; i++) {
cnt = 0; // 更新寄存器
for(ll j = 1; j <= m; j++) {
if(!v1[a[i][j]]) { // 如果这个点没访问过
b[j]++; // 更新该列贡献
v1[a[i][j]] = j; // 并更新最左侧的位置
} else if(v1[a[i][j]] && v1[a[i][j]] <= j) { // 如果这个位置访问过而且列数在子矩阵之内(对这次答案有贡献)
if(v2[a[i][j]]) { // 如果访问过第二次,说明这是第n>2次
if(v2[a[i][j]] > j) { // 判断这个第二次不是在子矩阵之内
b[v2[a[i][j]]]++; // 如果不是,贡献位置修改
b[j]--; // 因为不是第一或二次,贡献没用
v2[a[i][j]] = j; // 修改访问位置,确保v2最左
} // 判断这个第二次是在子矩阵之内,没关系,不用修改贡献
} else { // 判断没有访问过第二次,说明这是第二次
b[j]--; // 贡献没掉
v2[a[i][j]] = j; // 添加最左位置
}
} else if(v1[a[i][j]] && v1[a[i][j]] > j) { // 如果这个位置访问过而且列数在子矩阵之外(对这次答案无贡献)
b[j]++; // 说明这次就要有贡献了
b[v1[a[i][j]]] -= 2; // 子矩阵之外的就是第二次了,所以需要从+1变成-1
b[v2[a[i][j]]]++; // 如果有第n>2次,那么它的-1在现在的第二次减过了,补回来
v2[a[i][j]] = v1[a[i][j]]; // 更新
v1[a[i][j]] = j;
}
(cnt += b[j]) %= P;
(ans += cnt) %= P;
}
}
printf("%lld", ans);
}
T3 排列统计 GMOJ 1283
Description
对于给定的一个长度为n的序列{B[n]},问有多少个序列{A[n]}对于所有的i满足:A[1]~A[i]这i个数字中有恰好B[i]个数字小等于i。其中{A[n]}为1~n的一个排列,即1~n这n个数字在序列A[I]中恰好出现一次。
数据保证了至少有一个排列满足B序列。Input
输入的第1行为一个正整数N,表示了序列的长度。
第2行包含N个非负整数,描述了序列{B[i]}。Output
输出仅包括一个非负整数,即满足的{A[i]}序列个数。
Sample Input
3 0 1 3Sample Output
3Data Constraint
Hint
【样例说明】
对于A序列为1~3的全排列分别对应的B序列如下(冒号左边为A序列,冒号右边为对应B的序列)
1 2 3:1 2 3
1 3 2:1 1 3
2 1 3:0 2 3
2 3 1:0 1 3
3 1 2:0 1 3
3 2 1:0 1 3
所以有3个满足的A序列。
【数据说明】
对于20%的数据,有N≤8;
对于30%的数据,有N≤11且答案不大于20000;
对于50%的数据,有N≤100;
对于100%的数据,有N≤2000。
比赛考虑 dp,然后不会转移。
把题目转为矩阵就很明显了。
\(a[i]=j\) 表示为矩阵 \(A[i][j]=1\)
然后就是要求满足 \(A[1][1]\) 到 \(A[i][i]\) 有 \(b[i]\) 个 1 的矩阵个数。
这么一转换就很明显了。
因为矩阵的定义,一行一列不能有两个 1。这是很明显的。
假设我们填到:
1,0,?
0,1,?
?,?,?
需要补充上面的问号,就可以发现\(b[i]-b[i-1]\) 不能大于2,否则不能满足 一行一列不能有两个 1。
然后分类讨论dp即可。
这种转换题目的题考思维量,实在不会,就打个暴力吧……
#include <cstdio>
#include <cstring>
#include <algorithm>
#define ll long long
#define MX 100000000
using namespace std;
ll n;
ll a[2010];
ll b[2010];
struct node {
ll a[100010], len;
friend node operator *(const node &x, const int &y) {
node c;
memset(&c, 0, sizeof(c));
c.len = x.len;
for(ll i = 1; i <= c.len; i++) {
c.a[i] += x.a[i] * y;
if(c.a[i] >= MX) {
c.a[i + 1] += c.a[i] / MX;
c.a[i] %= MX;
c.len = max(c.len, i + 1);
}
}
for(ll i = c.len; i >= 1; i--) {
if(c.a[i] == 0) c.len--;
else break;
}
return c;
}
} ans;
int main() {
ans.a[1] = 1;
ans.len = 1;
scanf("%lld", &n);
for(ll i = 1; i <= n; i++) {
scanf("%lld", &b[i]);
ll delta = b[i] - b[i - 1];
if(delta == 0) {
ans = ans * 1;
} else if(delta == 1) {
ans = ans * (2 * i - 1 - 2 * b[i - 1]);
} else if(delta == 2) {
ans = ans * (i - 1 - b[i - 1]) * (i - 1 - b[i - 1]);
}
}
for(ll i = ans.len; i >= 1; i--) {
if(i == ans.len) printf("%lld", ans.a[i]);
else printf("%.8lld", ans.a[i]);
}
}
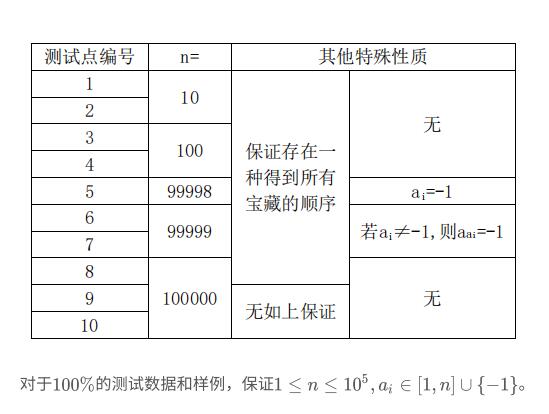
T4 近海之主(treasure) GMOJ 6363
肯定是数学题啦,我怎么可能会。
题目的样例都没有懂,如果会应该可以多水几分。(事实最后输出样例交到T2导致T2爆零555)
几次比赛前有一道题:搞笑的代码,中提到“数学期望=sigma(概率*权值)”
当时没有在意,这道题样例其实就是概率乘以权值:
然后就可以暴力了(为什么比赛时忘记了)
然后正解其实很简单,一个环肯定无解,然后一个树的某一个点如果能被打开,肯定是要按照:
祖先-祖先的儿子-祖先的儿子的儿子-祖先的儿子的儿子的儿子-……-这个点的父亲-这个点
要一环扣一环,如果一步走错,那么它的某一个孙子的门就打不开了……
那么这些点走下去总共有 \(A_n^n\) 种情况。
那么一环扣一环刚好走到这个点的概率为:
所以枚举每一个点走下去就行了。
总结:概率是什么?为什么一直考概率?
我要恶补。
#include <cstdio>
#define P 998244353
#define ll long long
ll n;
ll a[100010];
ll head[100010];
ll nxt[100010];
ll to[100010], cnt;
ll ans;
ll inv[100010];
ll fact[100010];
void addEdge(ll u, ll v) {
++cnt;
to[cnt] = v;
nxt[cnt] = head[u];
head[u] = cnt;
}
void dfs(ll u, ll dep) {
(ans += fact[dep]) %= P;
for(ll i = head[u]; i; i = nxt[i]) {
ll v = to[i];
dfs(v, dep + 1);
}
}
int main() {
// freopen("treasure.in", "r", stdin);
// freopen("treasure.out", "w", stdout);
scanf("%lld", &n);
inv[1] = 1;
fact[1] = 1;
for(ll i = 2; i <= n; i++) {
inv[i] = (((P - P / i) * inv[P % i]) % P + P) % P;
fact[i] = fact[i - 1] * inv[i] % P;
}
for(ll i = 1; i <= n; i++) {
scanf("%lld", &a[i]);
if(a[i] != -1) {
addEdge(a[i], i);
}
}
for(ll i = 1; i <= n; i++) {
if(a[i] == -1) {
dfs(i, 1);
}
}
printf("%lld", ans);
}