526互联

自底向上语法分析之 LR parser

发布时间 2023-08-14 01:37:47作者: shiys22

原博客发表于 \(\text{2022-12-02 19:28:50}\)。

自底向上（Bottom-Up）语法分析

短语：\(S\stackrel{*}{\Longrightarrow} \alpha A \delta, A \stackrel{+}{\Longrightarrow} \beta\)，则称 \(\beta\) 为句型 \(\alpha\beta\delta\) 相对于非终结符 \(A\) 的短语。

（句型：\((V_N \cup V_T)^*\)，句子：\(V_T^*\)）

直接短语：\(A \stackrel{+}{\Longrightarrow} \beta\) 改为 \(A \Longrightarrow \beta\)。

句柄：直接短语的 \(S\stackrel{*}{\Longrightarrow} \alpha A \delta\) 改为 \(S\overset{*}{\underset{rm}{\Longrightarrow}} \alpha A \delta\underset{rm}{\Longrightarrow} \alpha \beta \delta\)。不难发现，此时 \(\delta\) 一定是一个句子。

Lemma. 对一个文法来说，被这个文法识别的某个句型的句柄不唯一当且仅当文法是二义的。

归约：在当前串中找到某个与产生式右部相匹配的子串，将其用左部替换。经过若干次归约后，我们想要将输入串归约到开始符号 \(S\)。

Lemma. 一个句型可归约的子句型一定是其直接短语。

自底向上分析的实现技术：移进−归约（shift-reduce）分析技术。基本想法如下：

  • 从左到右扫描，依次读入字符。

  • 在合适的时候对当前的一个后缀进行归约。可知这样归约的一定是句柄，故得到的一定是一个最右推导。满足上两条的分析过程我们称为 \(\operatorname{LR}\) 分析（Left to right, Rightmost）。

  • 通过一个仅根据文法（故可以预处理）确定的特殊下推自动机来决定操作。根据当前状态、栈顶元素和剩余单词序列有如下操作

    • Reduce 对栈顶的短语进行归约。

    • Shift 从输入中读入一个字符放入栈顶。

    • Error 报错。

    • Accept 成功。

常用的 \(\operatorname{LR}\) 分析技术有：\(\operatorname{LR}(0), \operatorname{SLR}(1), \operatorname{LR}(1), \operatorname{LALR}(1)\)，我们之后会证明他们在文法能力上的一些性质，从而说明他们中每一个存在的意义。

不难发现，我们的处理方式是简单与直接的，这要求我们的文法有一些限制。下面介绍在不同限制的文法中我们如何得到这张分析表。

\(\operatorname{LR}(0)\) 文法

我们知道，我们想找到的实际上是每一个产生式的的句柄以及它们的归约关系。当我们完全匹配了一个句柄时立即归约，故其叫做 \(\operatorname{LR}(0)\) 文法。（提前预告，\(\operatorname{LR}(1)\) 便是在匹配了句柄时再多加一些考虑再归约）

所以我们需要进行维护的，是句柄的每一个前缀的匹配状态，也即，目前匹配到了哪些句柄的哪些前缀。为此我们引入活前缀（viable prefix）的概念。

\(S\overset{*}{\underset{rm}{\Longrightarrow}} \alpha A \delta, A \Rightarrow \beta\)，则 \(\alpha\beta\) 的任何前缀 \(\gamma\) 均为文法 \(G\) 的活前缀。

如果我们从反方向看，活前缀即，从 \(S\) 开始，每次仅展开一个非终结符，并把从这个位置开始的后缀全部删除，并保留之前的部分，这样递归若干轮。也就是说，由于每次只展开一个，这实际上是一个线性的而非嵌套的过程。从语法树上说，他和从根开始的一条链对应，内容便是这条链左边的并且是未被展开的东西。由此我们有

Lemma. 活前缀的集合是正规语言。

Prove by construction. 为了构造能够识别活前缀的自动机，我们来模拟这个反过程。

称 \(\operatorname{LR}(0)\) 项目表示在右侧某一位置添加一个圆点（某一种特殊字符）的产生式，表示已经分析过的串与该产生式匹配的位置。

如 \(A \to aBc\) 就有项目 \(A \to .aBc\)，表示还没有匹配，\(A \to a.Bc\)，表示匹配了 \(a\)，\(A \to aB.c\)，表示匹配了 \(aB\)，\(A \to aBc.\) 表示匹配完成。

那么，我们一步一步匹配活前缀，有两种情况

  • 匹配一个字符。它可能是终结符也可能不是。在语法树上体现为，将链向左挪。

  • 展开一个字符。在语法树上体现为，向儿子深入一步。

当然，我们要意识到一点，第二种操作，由于不需要输入，所以可能在一轮执行若干次。也即我们要将所有展开的可能全部放到一个状态里。这个过程叫做闭包。

比如有以下文法：

\[\begin{aligned} S &\to B \mid C \\ B &\to D \mid aE \\ C &\to F \mid bG \\ D &\to c \\ F &\to d \\ E &\to \ldots \\ G &\to \ldots \\ \end{aligned}\]

那么，\(a, b, c, d\) 都能够作为被接收的第一个字符。所以我们定义

一个项目集合 \(S\) 的闭包 \(\operatorname{CLOSURE}(S)\) 为以下操作生成的所有项目的集合

  • 若 \(A \to \alpha.B\beta\) 在集合中，则将所有的项目 \(\{B \to .\gamma\}\) 加入集合，\(\alpha, \beta, \gamma \in (V_N \cap V_T)^*\)，重复这一条直至不再有新项目产生。

我们在每一次执行了第一种操作时就做一次闭包，这样就完成了第二种操作。

并且，如果是 \(\operatorname{LR}(0)\) 文法，也即不向前查看字符的文法，我们可以发现一个项目与其闭包生成的项目是不可区分的，也即，执行多少次第二种操作是不可区分的。所以他们会在同一个状态里。

方便起见，在文法中新增一种非终结符 \(S'\)，新增一条文法 \(S' \to S\#\)，其中 \(\#\) 为字符串结束符号。将 \(S'\) 视作起始符号，防止 \(S\) 在文法中多次出现造成循环。这样的文法叫做增广文法。

那么，DFA 有一个初态，表示 \(S' \to .S\#\)。在语法树上，表示根。

之后我们执行如下步骤，生成 DFA 的其他状态

  • \(\operatorname{GO}(I, X)\)，表示 DFA 的第 \(I\) 个状态接受符号 \(X\) 后转移到的状态，为 \(J = \operatorname{CLOSURE}\left(\{A \to \alpha X.\beta \mid A \to \alpha.X \beta \in I\}\right)\)。

也就是说，如果两个项目是无法区分的，并且他们都要一个 \(X\)，那他们还是无法区分的。但是他们和那些不要 \(X\) 的区分开了。

我们不停地生成新的 \(J\)，直到不再生成了为止。除了表示空集合的那个状态，其他状态都是终态。这样我们就有了一个 DFA。

Theorem. 该 DFA 的语言是所有活前缀。

我们在前面已经以直观的形式说明了，这个 DFA 相当于不断执行两种操作，而执行两种操作和活前缀是等价的。

老师的 ppt 里的例子：

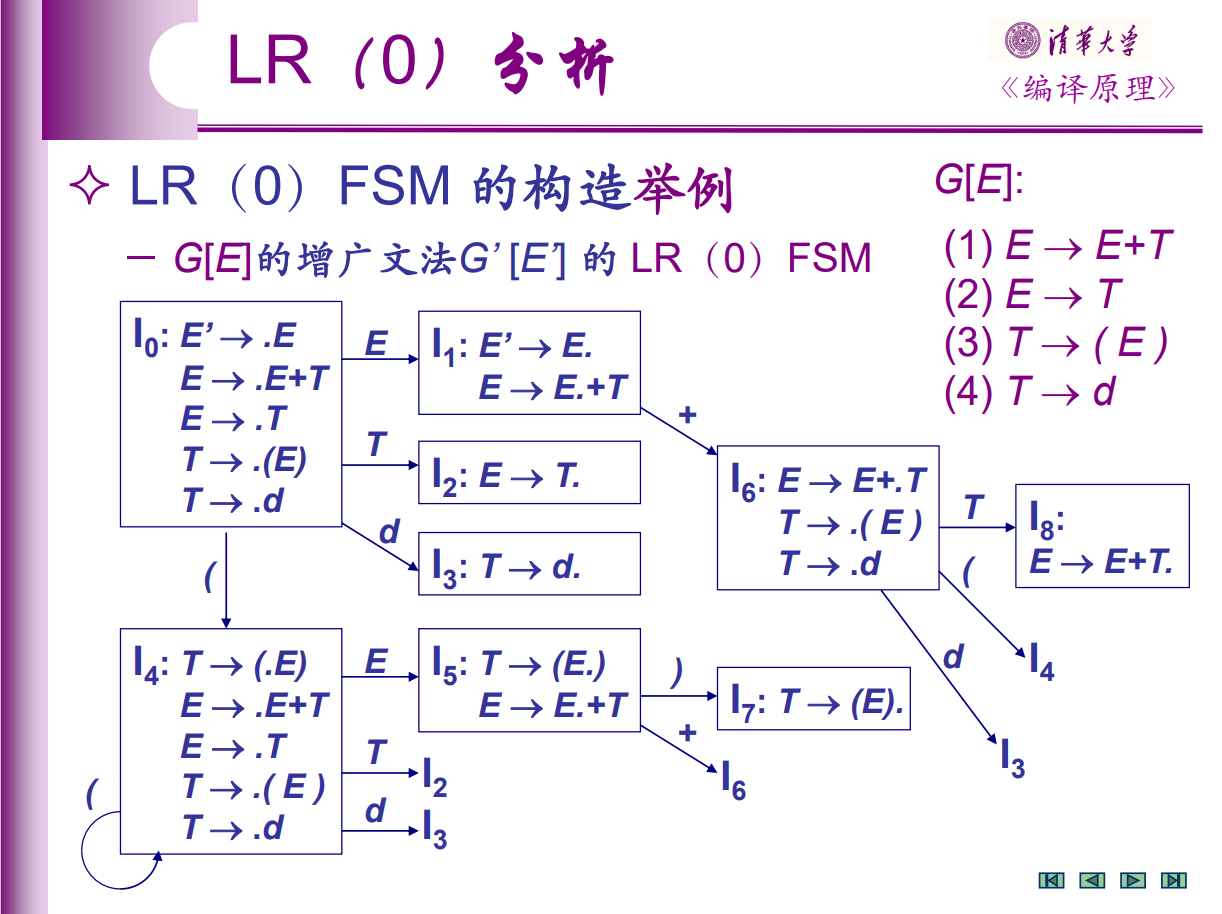
最后，关于这个自动机的状态，很可惜，它是指数级的。Ukkonen 给出的一个例子是

\[\begin{aligned} S' &\to A_0 \\ A_0 &\to 2 \\ A_{i-1} &\to 1A_ia_{i-1} & 1 \leq i \leq n \\ A_n &\to 1A_0a_n \\ A_i &\to 0A_ia_i & 1 \leq i \leq n \\ A_i &\to 0A_0a_i & 1 \leq i \leq n\end{aligned} \]

这样，DFA 的状态有 \(\Theta(2^n)\) 个。

在实践中，正常语言的 DFA，增长速度也就 \(O(n)\) 左右。

那么，我们回到最初的下推自动机那里。

  • Reduce 如果当前我们获得了一个句柄，那就立刻对栈顶的短语进行归约。此策略称作 \(\operatorname{LR}(0)\)，也即不顾及后面的任何符号就做出判断，与 \(\operatorname{LR}(k)\) 相对。后者顾及后 \(k\) 个字符再做出判断。之后，若我们使用了 \(A \to \beta\) 归约，我们把在 DFA 上走的最后 \(|\beta|\) 步撤回，并再在 DFA 上走出 \(A\) 这一步。

  • Shift 否则，从输入中读入一个字符放入栈顶。

  • Error 一旦 DFA 走到了空状态，报错。

  • Accept 成功。

我们用一张 \(\operatorname{LR}\) 分析表来描述这个下推自动机。

分析表分为两部分，\(\operatorname{ACTION}\) 表和 \(\operatorname{GOTO}\) 表。

\(\operatorname{ACTION}:(S \times V_T) \to P\)，其中 \(S\) 为栈的状态数，也即 DFA 的状态数；\(V_T\) 为字符，\(P\) 为一个操作。\(\operatorname{ACTION}[k, a]\) 表示栈顶为状态 \(k\)，当前输入字符为 \(a\) 时的操作，若等于 \(\mathbf si\)，表示将状态 \(i\) 移入栈顶，若等于 \(\mathbf rj\)，表示按文法第 \(j\) 条产生式归约，若等于 \(\mathbf{acc}\) 或 \(\mathbf{err}\)，则表示分析结束。

\(\operatorname{GOTO}:(S \times V_N) \to S\)。\(\operatorname{GOTO}[i, A] = j\) 表示归约了 \(A \to \beta\) 后，我们将栈顶的 \(|\beta|\) 个状态弹出，如果目前栈顶元素为 \(i\)，就把新状态 \(j\) 放入栈顶。

也就是说，\(\operatorname{ACTION}\) 描述了走终结符，\(\operatorname{GOTO}\) 描述了走非终结符。（好蠢啊，为什么不放在一起，不过为了符号统一性不得不服从了）

当我们发现，一张表的一个位置会有两种填法时，这个文法不是 \(\operatorname{LR}(0)\) 的。若是多个 \(\mathbf r\) 冲突，则称其为归约−归约冲突，比如 \(S \to aaS | aS | \varepsilon\)。若是 \(\mathbf r\) 和 \(\mathbf s\) 冲突，则称为移进−归约冲突，比如经典的 \(A \to \operatorname{if} A \operatorname{else} A| \operatorname{if} A | \varepsilon\)。

\(\operatorname{SLR}(1)\) 文法

\(\operatorname{LR}(0)\) 文法每当找到一个句柄时立即归约，而 \(\operatorname{SLR}(1)\) 多往前看一个字符，如果我们要归约 \(A \to \gamma\)，那么接下来的这个字符必须得是 \(\operatorname{Follow}(A)\) 里的元素才对。所以我们多加一个判断，即当且仅当接下来的一个字符是 \(\operatorname{Follow}(A)\) 中的，我们才用 \(A \to \gamma\) 进行归约。

\(\operatorname{LR}(1)\) 文法

但问题是，\(\operatorname{Follow}\) 是对非终结符说的，而不是对句柄说的。两个句柄后面可以出现的符号可能不同，即使他们是从同一个非终结符那里推来的。所以 \(\operatorname{SLR}(1)\) 的工作方式有所不妥。我们应该对每一种状态计算其 “\(\operatorname{Follow}\)”。

具体的做法是，我们将每一个项目后面署上可以接受的 \(\operatorname{Follow}\)，形如 \(A \to \alpha.\beta\textbf{, } a\)。

闭包的计算修改为

  • 若 \(A \to \alpha.B\beta\textbf{, }a\) 在集合中，则将所有的项目 \(\{B \to .\gamma\textbf{, }b\}\) 加入集合，其中 \(b=\operatorname{First}(\beta a)\)，\(\alpha, \beta, \gamma \in (V_N \cap V_T)^*\)，重复这一条直至不再有新项目产生。

DFA 的状态与转移修改为

  • \(\operatorname{GO}(I, X)\)，为 \(J = \operatorname{CLOSURE}\left(\{A \to \alpha X.\beta\textbf{, }a \mid A \to \alpha.X \beta\textbf{, }a \in I\}\right)\)。

初态为 \(S' \to S\textbf{, }\#\)，其中 \(\#\) 表示文本终结字符。

分析表修改为

  • Reduce 如果当前我们获得了一个句柄，并且当前的状态署上了向前看的字符，那就立刻对栈顶的短语进行归约。若我们使用了 \(A \to \beta\) 归约，我们把在 DFA 上走的最后 \(|\beta|\) 步撤回，并再在 DFA 上走出 \(A\) 这一步。

  • Shift 否则，从输入中读入一个字符放入栈顶。

  • Error 一旦 DFA 走到了空状态，报错。

  • Accept 成功。

这样，我们就能避免许多可避免的冲突。我们接下来要说明，这样的做法并非简单的剪枝，而是极其有意义的。有三条重要的结论

  • 一个语言的 \(\operatorname{LR}(1)\) 文法的存在性与 \(\operatorname{DPDA}\)（确定下推自动机）的存在性等价。满足存在 \(\operatorname{LR}(1)\) 文法或 \(\operatorname{DPDA}\) 的语言称作确定上下文无关文法（Definite CFG）。

  • 一个语言的 \(\operatorname{LR}(1)\) 文法的存在性与 \(\operatorname{LR}(k)\) 文法的存在性等价。（这一点不难猜出，因为二义文法 \(\operatorname{LR}(k)\) 是怎么也无法解决的，所以）

  • 任何 \(\operatorname{LL}(k)\) 文法都是 \(\operatorname{LR}(k)\) 文法。

这三条的证明，等我会了再说，之后会补上。（或许是期末后？

所以实际上，\(\operatorname{LR}(k)\) 是表示能力相当强的语言了，有许多编程语言都是 \(\operatorname{LR}(k)\) 的（C++ 是著名的一个反例）。