526互联

1483. Kth Ancestor of a Tree Node (Hard)

发布时间 2023-06-18 16:55:38作者: zwyyy456

Description

1483. Kth Ancestor of a Tree Node (Hard) You are given a tree with n nodes numbered from 0 to n - 1 in the form of a parent array parent where parent[i] is the parent of ith node. The root of the tree is node 0. Find the kth ancestor of a given node.

The kth ancestor of a tree node is the kth node in the path from that node to the root node.

Implement the TreeAncestor class:

  • TreeAncestor(int n, int[] parent) Initializes the object with the number of nodes in the tree and the parent array.
  • int getKthAncestor(int node, int k) return the kth ancestor of the given node node. If there is no such ancestor, return -1.

Example 1:

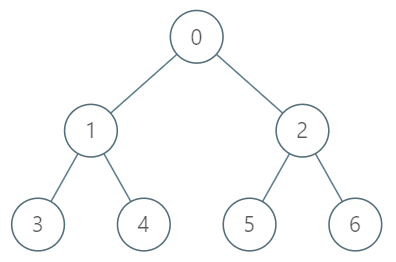
Input
["TreeAncestor", "getKthAncestor", "getKthAncestor", "getKthAncestor"]
[[7, [-1, 0, 0, 1, 1, 2, 2]], [3, 1], [5, 2], [6, 3]]
Output
[null, 1, 0, -1]

Explanation
TreeAncestor treeAncestor = new TreeAncestor(7, [-1, 0, 0, 1, 1, 2, 2]);
treeAncestor.getKthAncestor(3, 1); // returns 1 which is the parent of 3
treeAncestor.getKthAncestor(5, 2); // returns 0 which is the grandparent of 5
treeAncestor.getKthAncestor(6, 3); // returns -1 because there is no such ancestor

Constraints:

  • 1 <= k <= n <= 5 * 10⁴
  • parent.length == n
  • parent[0] == -1
  • 0 <= parent[i] < n for all 0 < i < n
  • 0 <= node < n
  • There will be at most 5 * 10⁴ queries.

Solution

The simplistic notion entails gradually searching for the parent node, resulting in a time complexity of O(n). Therefore, the overall time complexity becomes O(n^2), leading to a potential TLE (Time Limit Exceeded). Thus, we need to devise a more efficient approach for finding the parent node with a lower time complexity of O(log n). This leads us to contemplate a binary-like strategy.

For instance, let's assume we need to find getKthAncestor(1, 8). We can first determine x = getKthAncestor(1, 4) and then compute getKthAncestor(x, 4). This approach bears resemblance to dynamic programming.

Let's define $dp[i][j]$ as the i-th node's ancestor at the $2^j$ position, where $dp[i][j] = dp[dp[i][j-1]][j]$ and $dp[i][0] = parent[i]$.

During initialization, we can initialize the $dp[i][j]$ array. Given that $1 \leq k \leq n \leq 5 * 10^4$, the first dimension of the $dp$ array should have a size of n, and the second dimension's size can be set to logk = 20. In the constructor, we compute the $dp[i][j]$ array, taking care to handle the case when $dp[i][j] = -1$.

In the getKthAncestor() function, we can employ bitwise operations to calculate the parent node: $pa = dp[pa][i]$, provided that $((1 << i) & k) \neq 0$. If we compute $pa = -1$, we simply return pa.

Code

class TreeAncestor {
  public:
    TreeAncestor(int n, vector<int> &parent) :
        cnt_(n), index_(0), dp(n) {
        int x = 0;
        for (int i = 0; i < parent.size(); ++i) {
            parent_.push_back(parent[i]);
        }
        for (int i = 0; i < cnt_; ++i) {
            for (int j = 0; j < logk; ++j) {
                dp[i].push_back(-1);
            }
        }
        for (int i = 0; i < cnt_; ++i) {
            dp[i][0] = parent_[i];
        }
        while (index_ < logk) {
            for (int i = 0; i < cnt_; ++i) {
                if (dp[i][index_] != -1) {
                    dp[i][index_ + 1] = dp[dp[i][index_]][index_];
                }
            }
            x *= 2;
            ++index_;
        }
    }
    int getKthAncestor(int node, int k) {
        int pa = node;
        for (int i = 0; (1 << i) <= k; ++i) {
            if (((1 << i) & k) != 0) {
                pa = dp[pa][i];
                if (pa == -1) {
                    return pa;
                }
            }
        }
        return pa;
    }

  private:
    int cnt_;
    vector<int> parent_;
    int index_;
    vector<vector<int>> dp;
    const int logk = 20;
};