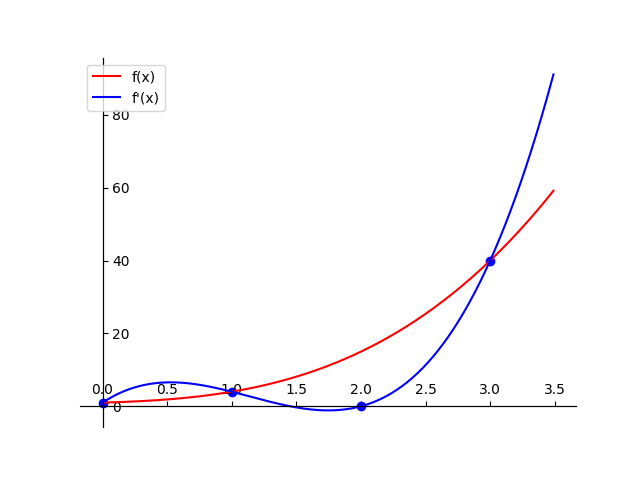
本文主要参考资料:找通项的终极方法!让每个人都能听懂的【拉格朗日插值法】_哔哩哔哩_bilibili
回顾,多项式的系数表示法和点值表示法:FFT(快速傅立叶变换)学习 - Isakovsky - 博客园 (cnblogs.com)
从系数表示法到点值表示法的运算叫做求值运算,从点值表示法到系数表示法的运算叫做插值运算.
假设有$k$个横坐标不同的点,记这$k$个点为$(x_0,y_0),(x_1,y_1),\cdots,(x_{k-1},y_{k-1})$
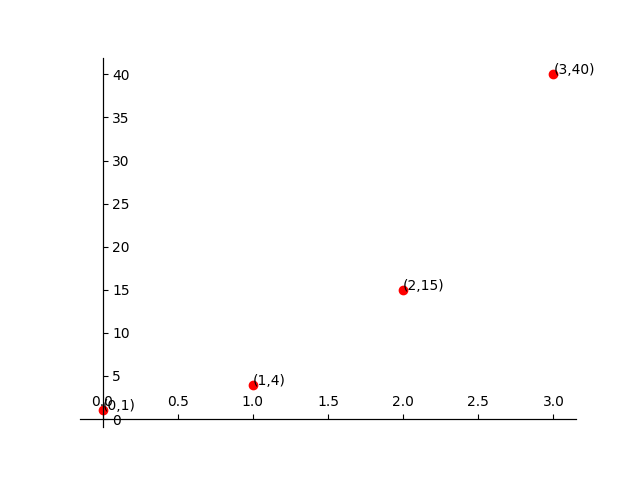
Lagrange插值的功能就是从$k$个横坐标不同的点中唯一确定一条$k-1$次多项式的曲线.$k$个自由变量正好对应着$k-1$次多项式中的$k$个参数.

Lagrange插值的思想是,对于每个$(x_i,y_i)$,找到一条$k-1$次曲线$p_i(x)$,称为插值基函数,使得其在$x=x_i$处的值为$y_i$,$x=x_0,x_1,\cdots,x_{i-1},x_{i+1},\cdots,x_{k-1}$处的值为$0$,

然后将这$k$条曲线相加,
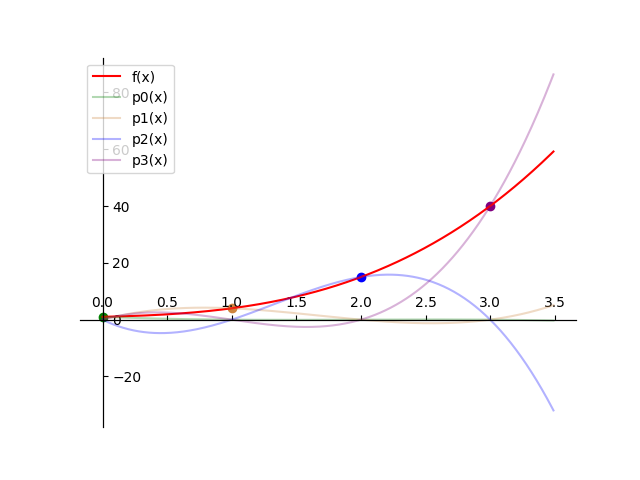
接下来的问题就是,对于每个$(x_i,y_i)$,如何找到插值基函数$p_i(x)$,使得其在$x=x_i$处的值为$y_i$,$x=x_1,x_2,\cdots,x_{i-1},x_{i+1},\cdots,x_k$处的值为$0$呢?
以$x=x_1$为例,要找到曲线$p_1(x)$,使得$p_1(x_0)=p_1(x_2)=p_1(x_3)=0$,$p_1(x_1)=y_1$
观察这个式子:
$$\frac{x-x_0}{x_1-x_0}$$
这个式子在$x=x_1$处的值为$1$,在$x=x_0$处的值为$0$,
类似地,
$$\frac{x-x_2}{x_1-x_2}$$
在$x=x_1$处的值为$1$,在$x=x_2$处的值为$0$,
$$\frac{x-x_3}{x_1-x_3}$$
在$x=x_1$处的值为$1$,在$x=x_3$处的值为$0$,
发现规律没有?
$$\frac{x-x_j}{x_i-x_j}$$
在$x=x_i$处的值为$1$,在$x=x_j$处的值为$0$,
只需要将它们乘起来
$$\Pi_{j=0,1,\cdots,i-1,i+1,\cdots,k-1}\frac{x-x_j}{x_i-x_j}$$
这个式子中,在$x=x_i$处的值为$1$,在$x=x_0,x_1,\cdots,x_{i-1},x_{i+1},\cdots,x_{k-1}$处的值为$0$,
然后再乘上一个$y_i$,便得到了
$$p_i(x)=y_i\cdot\underset{j=0,1,\cdots,i-1,i+1,\cdots,k-1}{\Pi}\frac{x-x_j}{x_i-x_j}$$
由此便得到了Lagrange插值公式:
$$f(x)=\Sigma_{i=0}^{k-1}p_i(x)=\Sigma_{i=0}^{k-1}(y_i\cdot\underset{j=0,1,\cdots,i-1,i+1,\cdots,k-1}{\Pi}\frac{x-x_j}{x_i-x_j})$$
注意,Lagrange插值不允许数据带有噪音,否则会对运算结果产生较大影响,这被称为Runge现象.(或者更笼统地称之为过拟合)