贪心（不同情况下有不同策略）题单报告

书接上回。

感觉这个标题起得云里雾里的颇有上次讲的“反悔自动机”的奇妙风范，坏了会回旋镖插我自己身上了（

感觉这样的贪心很厉害。什么叫不同情况下有不同策略呢？就是说你要分讨，分讨的每一种情况我们都要保证这是当前的最优解。这听起来是不是还是很扯，其实这是为了方便我自己看的，所以我瞎扯瞎扯问题不大(/ω＼)

这个就当是我自己瞎扯的吧(/ω＼)

P2587

田忌赛马，典题。

无论这道题多么经典和简单，如果完全没有接触，我们很难找到解法。所以让我们来发散的思考思考

我们战术分析一下老祖宗流传给我们的田忌赛马策略，假设 A 代表田忌，B 代表齐王

A 0.5 1.5 2.5
B 1 2 3

如果硬碰硬，那么田忌永远打不赢，所以田忌换了一个策略，用 0.5 兑 3，然后用 1.5，2.5 分别赢了 1 和 2。

这告诉我们可以这样来操作，除了一味地要赢以外，还可以用最小的去兑对方最大的。

这样的操作让我们得到一些东西

1. 这道题是贪心没跑了。
2. 我们可以先排个序。
3. 我们有这样的贪心策略

• 要赢最多场次。
• 在当前赢了最多场次的前提下，我们要尽量用最小的代价赢。用上面的例子来说，很显然用 2.5 赢对方的 1 实在是太浪费了。

我们可以维护 \(min1, max1\) 代表当前田忌的最小值最大值的下标（是下标），\(min2, max2\) 代表齐王的最小值最大值下标。

很显然，我们会选择用最小对最小（最大对最大也可以）

如果用最小对最小，那么会有三种情况

1. \(a(min1) > b(min2)\) 要赢就赢，这时候肯定是最小的代价来赢的。
2. \(a(min1) < b(min2)\) 这个时候 \(min1\) 肯定谁都打不过，那么我们怎么办？我们直接让它兑 \(b(max2)\) 吗？不，万一 \(a(max1) > a(max2)\) 呢？能直接赢下一场胜利岂不更好？
   但这也启发我们，来比较 max
   • \(a(max1) > b(max2)\)，那么就赢了它。
   • \(a(max1) < b(max2)\) 那么此时没有选择应为 \(min1\) 谁也打不过，所以我们就用它兑掉 \(max2\)。
   • \(a(max1) = b(max2)\) 这是一个值得玩味的情况，它看上去就没那么显然了。比如说田忌的最小兑齐王的最小，然后我用最大的和齐王的打平？但是这肯定不如我用最小兑最大来的优。还是那个道理，\(min1\) 谁也打不过，所以兑最大比兑最小来的划算，而且此时 \(b(max2)\) 就会更新成 \(b(max2')\) 并且 \(b(max2') \le b(max2)\)。\(max1\) 可能能赢也可能打平，反正不会输，最坏情况下是 \(-1\)，但是更好一点的情况是 \(0\)。所以我们选择兑一局
3. \(a(min1) = b(min2)\)，打平。学习上面的思路，我们比较 max
   • \(a(max1) > b(max2)\)，赢了它。
   • \(a(max1) < b(max2)\)，\(min1\) 谁也打不过。是平局一下还是兑 \(b(max2)\) 呢？
     平局的话，那么 max1 要输，所以是价值是 \(-1\)。
     兑的话，\(min1\) 要输一局，然后 \(max1\) 肯定会赢或平（起码不会输），最坏的话价值是 \(-1\)，最好的话输一局赢一局就刚好是 \(0\) 了，就更优了。
     所以我选择兑一局。
   • \(a(max1) = b(max2)\) 全平。和上面一样，考虑平局一下和兑一下。
     平局的话，那么就价值是 \(0\)。
     兑一下的话，\(min1\) 可能输也可能平，\(max1\) 可能赢也可能平，最坏的话价值是 \(0\)。
     值得一提的是这种情况最好价值也是 \(0\)。因为如果 \(min1\) 平 \(max2\) 说明 \(a\) 和 \(b\) 里面所有元素都相等。这个时候 \(max1\) 是平的，所以最好价值还是 \(0\)。
     其实这两种情况等价，不过为了方便我们还是可以选择兑一局（因为兑一局的情况更多一些）

这是代码

#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
int a[N], b[N];
void init() {
	int n; cin >> n;
	for(int p = 1; p <= n; p++)
		cin >> a[p];
	for(int p = 1; p <= n; p++)
		cin >> b[p];
	sort(a + 1, a + n + 1);
	sort(b + 1, b + n + 1);
	int min1 = 1, min2 = 1, max1 = n, max2 = n, cnt = 0;

	for(int p = 1; p <= n; p++) {
		if(a[min1] > b[min2]) min1++, min2++, cnt += 2;
		else if(a[min1] == b[min2]) {
			if(a[max1] > b[max2]) max1--, max2--, cnt += 2;
			else if(a[max1] < b[max2]) min1++, max2--;
			else {//a[max1] == b[max2]
				if(a[min1] == b[max2]) cnt++;
				min1++, max2--;
			}
		}
		else min1++, max2--;
	}
	cout << cnt << ' ';

	min1 = 1, min2 = 1, max1 = max2 = n, cnt = 0;
	for(int p = 1; p <= n; p++) swap(a[p], b[p]);

	for(int p = 1; p <= n; p++) {
		if(a[min1] > b[min2]) min1++, min2++, cnt += 2;
		else if(a[min1] == b[min2]) {
			if(a[max1] > b[max2]) max1--, max2--, cnt += 2;
			else if(a[max1] < b[max2]) min1++, max2--;
			else {//a[max1] == b[max2]
				if(a[min1] == b[max2]) cnt++;
				min1++, max2--;
			}
		}
		else min1++, max2--;
	}
	cout << 2 * n - cnt << endl;
}
int main() {

    // freopen("read.in", "r", stdin);
    // freopen("write.out", "w", stdout);
	init();
}

P4785

超级好的一道题，吹爆！

这个报告希望可以更加详细明确的探讨一下这道题的思维过程，欢迎各位来探讨交流 qwq

首先我们战术观察一下这道题目。Democy 子曰，字典序最小就是贪心，所以我们这道题的大框架就是贪心。我们看到这个交换很有意思，\(a_n\) 和 \(a_{\lfloor\frac{n}{2}\rfloor}\) 换。。如果你二叉树学的很扎实或者做过相似的题目（举个例子这题）那么我们就会想到把它放到一个完全二叉树上去。那么每次交换操作就是交换一个儿子和父亲了。

现在我们已经确定了大框架：在完全二叉树上跑贪心。

然后我们继续深入思考。

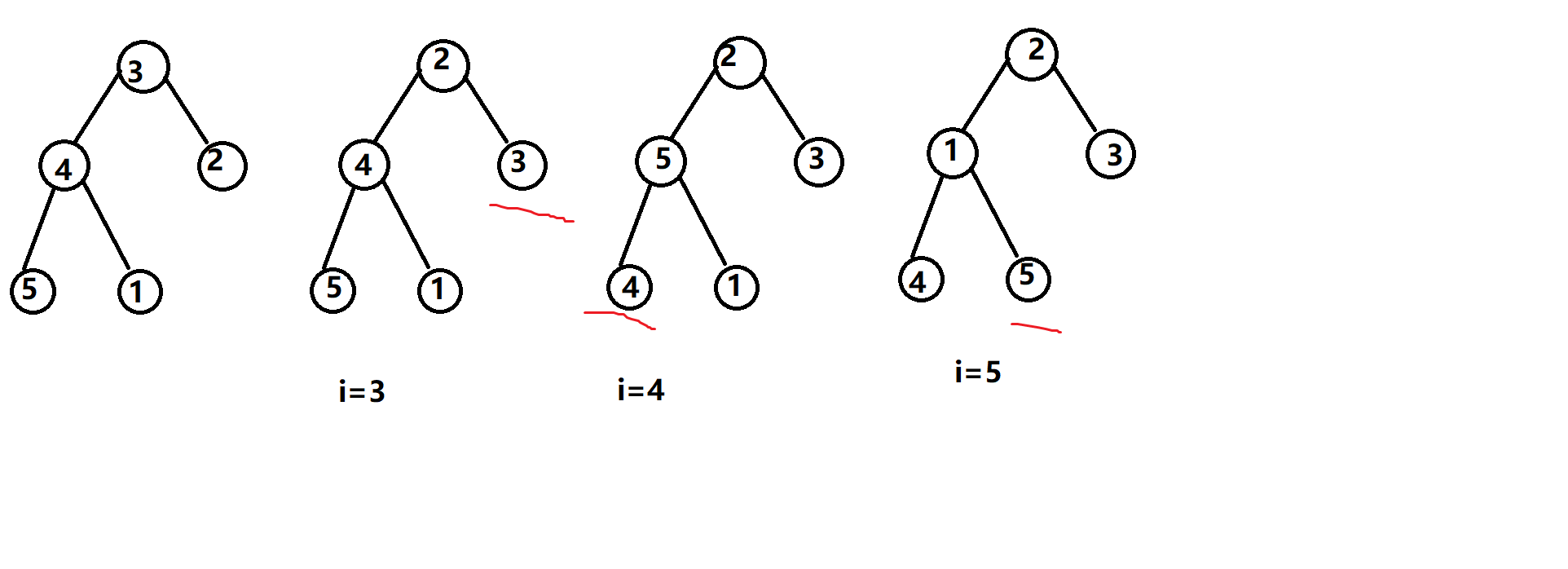
这道题让我们字典序最小，其实是什么？是我从上到下从左到右把每个点的值串下来的最小字典序。

每次交换儿子和父亲，而且是从 \(i = 2\sim n\) 这样依次交换，放到完全二叉树上，就是从上到下，从左到右的交换。

拿样例举例子，像这样：

这道题的操作是交换，从上到下从左到右交换自己的父亲，这有什么性质？我们可以把一个点通过它的儿子们不断的交换交换交换到下面去，但是不可能把它通过儿子交换上来，这就颇有几分“不同层之间互不干扰”的意味（当然还是有一定干扰的）。在不同子树之间又是基本上互不影响的，我们可以根据不同的子树划分子问题。这就启发我们每次考虑一个父亲和它的两个儿子，然后递归下去。像这样

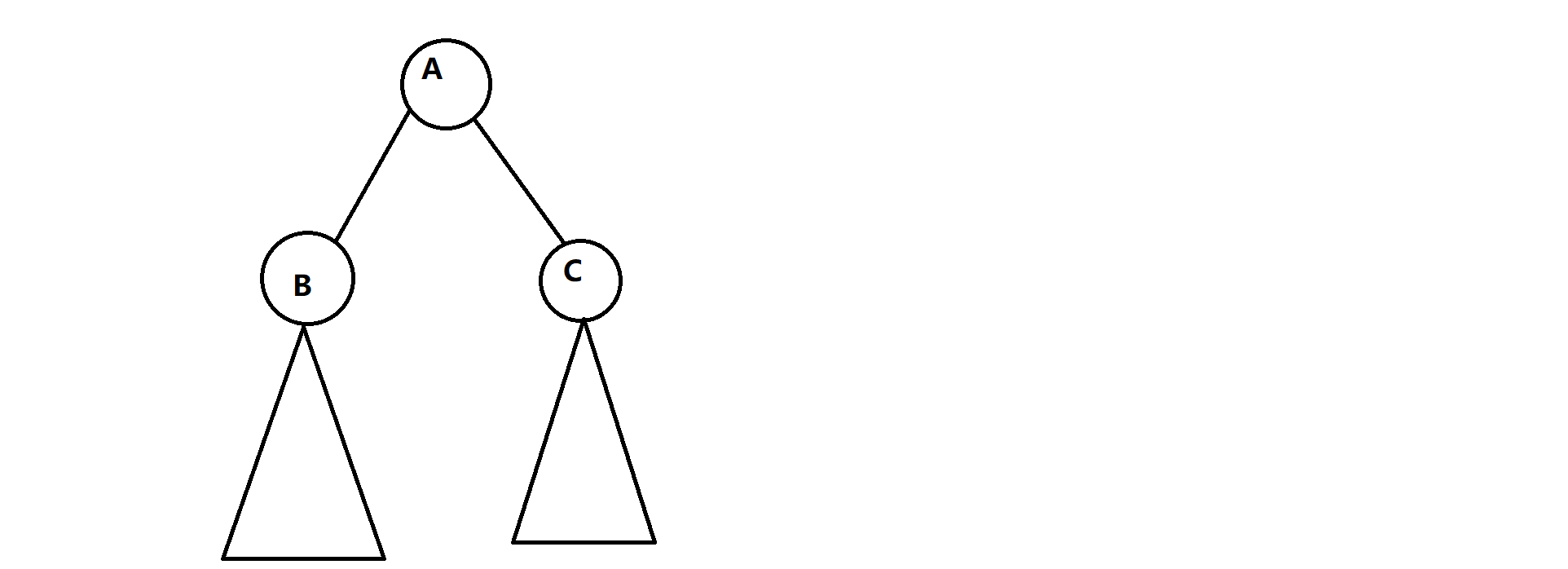
由于我们不可能把 A 点换上去，所以一个子树是基本独立的。然后呢？我们肯定会考虑 B，C 怎么换。这一共有四种换发

1. 不换
2. B 换 C 不换
3. B 不换 C 换
4. B，C 都换。

通过手玩不难找到这四种情况对应的序列

1. A-B-C
2. B-A-C
3. C-B-A
4. C-A-B

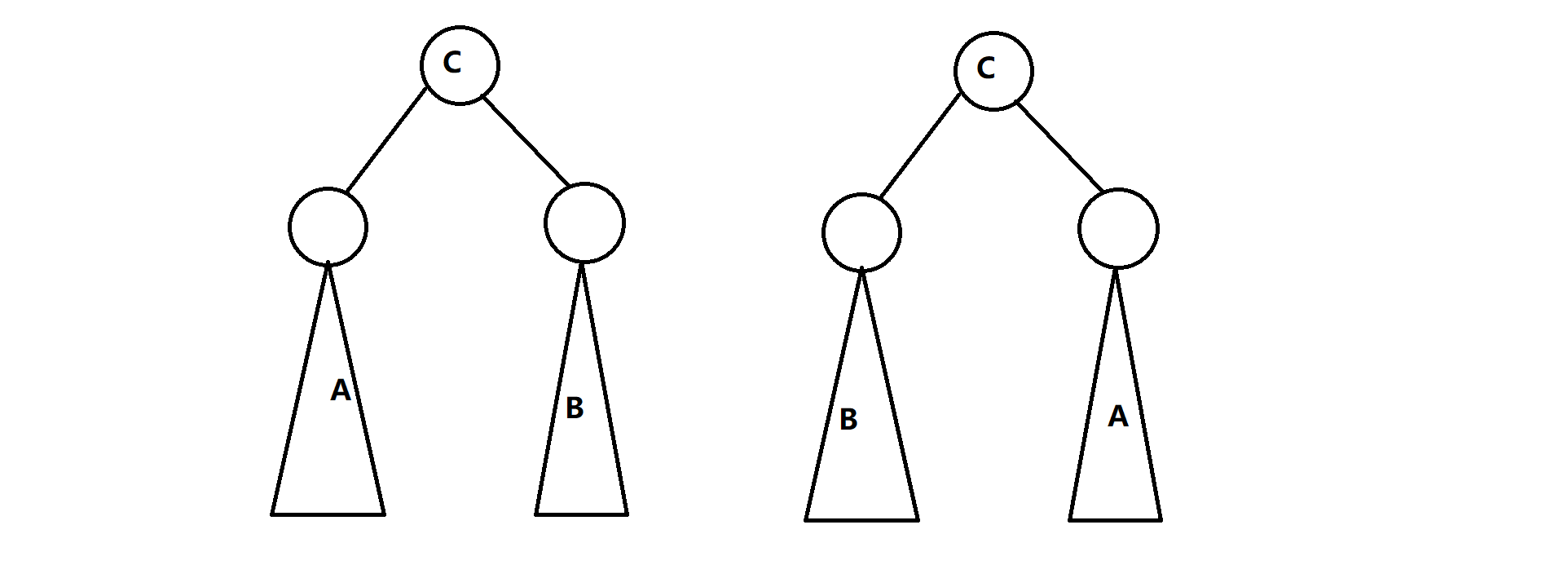
为了字典序最小，首先根肯定要最小，这很容易理解。也就是说，如果 \(a(A)\) 或 \(a(B)\) 是 \(a(A), a(B), a(C)\) 三者中的最小者，那么我们可以直接确定。但是 \(C\) 呢？A，B 可以在子树中继续交换，这就不简单了。因为我们并不知道 A 和 B 放在哪。我们来幻想一下 A 在左子树 B 在右子树和 A 在右 B 在左的情况。画一下图

我们会发现这样一点，我们只需要知道 A，B 在左右子树中最优能在哪个位置就好了。这个位置是在整个二叉树中的编号。我们肯定希望这里面小的的编号小。不妨设 \(a(A) < a(B)\)。令 \(a(A)\) 在左子树的最优位置是 \(pos1\)，在右边的是 \(pos2\)。如果 \(pos1 < pos2\) 就让 A 去左边，反之去右边。\(a(A) > a(B)\) 同理。

那么我们怎么求这个 \(pos1\) 和 \(pos2\) 呢？这个子问题让我们很想 dp 一下（雾，我们可以定义 \(f(u, val)\) 代表以编号 \(u\) 为根的子树根节点的值变成了 \(val\) 后，\(val\) 所处的最优位置。这个问题可以通过上面的策略解决。这样一个 \(val\) 只可能出现在 \(u\) 的祖先上，所以一共只有 \(O(n\log_2 n)\) 种状态，记忆化一下时间复杂度 \(O(n\log2_n)\)。这样说很笼统，但是重新叙述一遍又太累赘，所以具体看代码吧 awa

#include <bits/stdc++.h>
using namespace std;
const int MAXN = 4e5;
int a[MAXN + 10], n;
unordered_map <int, unordered_map <int, int> > f;
int getpos(int now, int val) {
	if(!a[2 * now]) return now;
	if(!a[2 * now + 1]) {
		if(a[2 * now] < val) return 2 * now;
		else return now;
	}
	if(f[now][val]) return f[now][val];

	int A = val, B = a[2 * now], C = a[2 * now + 1];
	if(A < B && A < C) return f[now][val] = now;
	else if(B < A && B < C) return f[now][val] = getpos(2 * now, val);
	else {
		if(A < B) return f[now][val] = min(getpos(2 * now, val), getpos(2 * now + 1, val));
		else {
			if(getpos(2 * now, B) > getpos(2 * now + 1, B))
				return f[now][val] = getpos(2 * now, val);
			else return f[now][val] = getpos(2 * now + 1, val);
		}
	}
	return f[now][val];
}
void dfs(int now) {
	if(!a[2 * now]) return ;
	if(!a[2 * now + 1]) {
		if(a[now] > a[2 * now]) swap(a[now], a[2 * now]);
		return ;
	}
	int &A = a[now], &B = a[2 * now], &C = a[2 * now + 1];
	if(A < B && A < C) dfs(2 * now), dfs(2 * now + 1);
	else if(B < A && B < C) {
		swap(A, B);
		dfs(2 * now), dfs(2 * now + 1);
	}
	else {
		int aa = A, bb = B, cc = C;
		if(getpos(2 * now, min(A, B)) < getpos(2 * now + 1, min(A, B))) B = min(aa, bb), C = max(aa, bb);
		else B = max(aa, bb), C = min(aa, bb);
		a[now] = cc;
		dfs(2 * now), dfs(2 * now + 1);
	}
	return ;
}
void init() {
    scanf("%d", &n);
	for(int p = 1; p <= n; p++)
		scanf("%d", &a[p]);

	dfs(1);
	for(int p = 1; p <= n; p++)
        printf("%d ", a[p]);
}
int main() {
	init();
}

P6927

明天填坑 awa（）

本栏目推荐文章
• 解题报告P2501 [HAOI2006] 数字序列
• [JMeter] JMeter的测试报告格式转换(.jtl => html)
• 北京高院--在总包方实质审查每一个劳务班组工资的情况下，法院应认定总包付清款项后不应当轻易对已经实质确认的班组费用承担责任
• 四川高院--即使工程款已经结清，在总包方非实质审查结并确认清班组工资情况下，仍应对工人工资承担责任。
• 【专题】2022云上新型电力系统报告PDF合集分享（附原数据表）
• 【专题】新零售下品牌消费者为中心的数字化转型报告PDF合集分享（附原数据表）
• 【专题】2023中国经济高质量发展中的商业地产趋势与机遇专题报告PDF合集分享（附原数据表）
• 系统竣工报告模板
• 软件测试报告模板
• 快速查看显卡使用情况和占用用户

下有 策略 情况 报告下有 策略 情况 报告 数据表 研究报告 趋势 策略 情况 报告 动态 经济 下有 菱形 布局 情况 报告 两个 项目 下有 仓库 多个 系统 下有 附件 下有 函数 对象 内存 下有 图像 场景 技术 情况