写在前面

首先，本人很菜。

其次，本文只也许够应付考试，个人使用。而且其实就是ppt内容只是我自己喜欢这样整理。虽然全力理解内容且认真书写但也可能存在错误，如有发现麻烦指正，谢谢?

最后，因为不知道考试怎么考，本人的复习方式是照着目录讲一遍自己的理解+写伪代码（如果来的及会再做一个综合纯享版），再做一下上课讲过的例题和作业(印象里只有主定理、FFT、网络流上课练习+分治和动规两次作业)。

文章持续更新中，链接在此：算法设计与分析 - 随笔分类 - hotaru蛍 - 博客园 (cnblogs.com)，或许考前能发完也可能发不完。

祝我们好运?

分治

三步走：

1. 分解：大问题分解为一组与大问题相似但是规模变小的子问题。
2. 解决：递归求解。如果足够小直接求解。
3. 合并：子问题的解组合成原问题的解。

主定理

1.定理内容（简化形式）

1. “abc”: 将问题分解为a个子问题、每个问题规模是原问题的1/b、分解和合并的时间为n^c
2.  递归形式：T(n) = aT(n/b) + n^c  , a>=1 , b>=2 , c>0 ,T(1)=O(1)
3.  应用：比较a和b^c
   1.  

2. 定理内容（完全态）

3. 一些例题

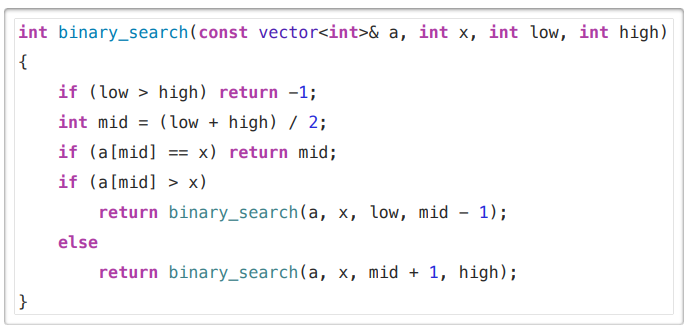
二分搜索

1. 问题描述

一个已排序数组a[1...n]找出元素x，存在则返回下标不存在返回-1.

2. 分治

1. 分解：Left，中间元素a[mid]，Right
2. 解决：如果a[mid]=x则返回mid；否则根据大小判断递归求解Left或Right。如果数组为空返回-1。
3. 合并：不需要额外工作。

3. 时间复杂度分析

T(n)<=T(n/2)+O(1)  ,T(1)=1 →  T(n)<=T(n/2)+1

T(n)<=T(n/2)+1 <=T(n/4)+2 <=... <=T(n/2^k)+k

令n = 2^k ，T(n)<=T(1)+logn = 1+logn

T(n) = O(logn)

4. 正确性分析(归纳假设)

计数

1. 问题描述

一个已排序数组a[1...n]，返回元素x的次数。

2. 方案分析

1. 考虑直接二分

  先找到x：O(logn)

  → 向左向右扫描找到左右边界确定有s个x

  总复杂度：O(logn + s)，最坏情况下是Θ(n)。

例：

2. 改进：找到x的左右边界（三步走）

1.  分解：a[l .. r]分为a[l...m-1]和a[m...r]两个部分
2.    解决，以右边界为例(左边界)：
   1. 基本情况：l>r 返回-1
   2. a[m]=x，若m=n (m=0) 或者a[m+1]>x (a[m-1]<x) ,返回m
   3. a[m]<x : 递归 a[l...m-1]； 否则递归a[m...r]
3. 合并：不需要额外工作

时间复杂度：O(logn)

选择（中位数）

1. 问题描述

 找到数组a[1...n]的中位数

→ 增强归纳假设 → 找到找到数组a[1...n]的第k小的数

2. 方案分析

1.基于排序直接解决

O(nlogn)

2. 随机主元递归（不全排）

1. 思路：每次随机选一个主元v，通过v将数组划分为 小于v  等于v  大于v三个部分；迭代判断k是否在v下标范围内。
2. 表示如下（注意右侧第k小需要减去左侧和中间）：
   
3. 分析时间复杂度：
   1. 划分的时间复杂度O(n)，空间复杂度O(1)
   2. 如果每次选的主元刚好让左侧右侧数目相等(但不可能)：T(n)=T(n/2)+n → T(n) = O(n)
   3. 随机选取（本方法）：
      1. 最好情况：O(n) （一次就成）
      2. 最坏情况：T(n) = T(n-1)+n → T(n) = O(n²)
      3. 平均情况：O(n) （可以证明，但没讲）

3. 进一步优化主元选择

1. 主元选择步骤：
   1. 将数组分成五份。(n/5向下取整有可能有六份)
   2. 取五份子数组各自的中位数，5个。
   3. 选这五个中位数中的中位数作为主元v
2. 复杂度分析：
   1. 至少有一半中位数<= v 
      → 至少有 └((n/5)/2)┘ =  └(n/10)┘个中位数<= v
      → 至少有3└(n/10)┘个中位数<= v
   2. 至少有一半中位数>= v 
      → 至少有 └((n/5)/2)┘ =  └(n/10)┘个中位数>= v
      → 至少有3└(n/10)┘个中位数>= v
   3. 故递归时，从最多n - 3└(n/10)┘个数中选取下一个v
   4. T(n):从n个元素选择第k小元素的比较次数，
      T(n) <= T(└(n/5)┘) + T( n- 3└(n/10)┘) +11/5 · n
3. T(n)<=44n

最近点对

1. 问题描述

给定⼆维平面上的 个点，找到距离最近的⼀对点

2. 方案分析

1.穷举

O(n²)

2.排序+扫描

O(nlogn)

3.分治

1. 三步走：

   1.  分解：将空间中点构造垂线分为左右两部分

   2.  解决：递归求解左右两侧最近点对

   3.  合并：找到跨垂线的最近点对，返回三者最小的。

2. 如何找到跨垂线的点对
   

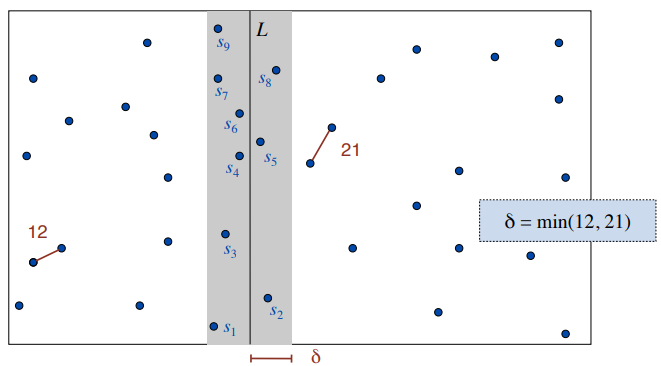
   1.  分别找到左侧最近点对距离δ1，右侧最近点对距离δ2，min(δ1，δ2) = δ
   2.    故对于跨左右垂线的仅需要考虑L<δ的点
      1. 插播一个事实：把带宽为2δ带状区域内的点按照纵坐标从小到大排序，只需要考虑距离每个点最近的七个点的距离，故7n次计算即可得到跨左右的最近点对。
            至于为什么：
         
   3. 基于这个事实，可以得到整个基于分治思想的最近点对算法（未优化版）伪代码(?)如下：
      

      Close_pair(p1...pn)
        将所有的点依据横坐标分为L和R两个部分，每个部分有n/2个点   //O(n)
         δ1 ← Close_pair(L)  // T(n/2)
         δ2 ← Close_pair(R)  // T(n/2)
         δ = min(δ1，δ2)     
         A ← 所有距离分割线小于δ的点   //O(n)
         A中坐标按照纵坐标排序   //O(nlogn)
         对于A中每个点计算其与后续7个点的距离，如果距离小于δ则更新δ。
         return δ

       

      时间复杂度分析：T(n) = 2T(n/2) + O(nlogn)   =  O(nlog²n)
      
      
   4. 考虑如何优化： 保持输入有序
      
      
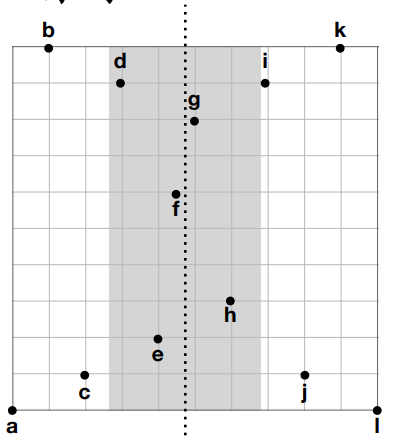
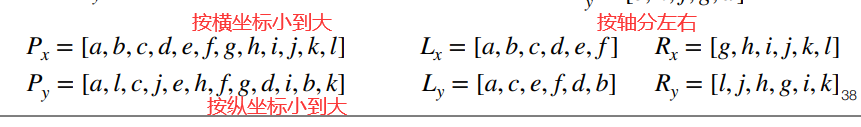
      优化后的伪代码：
      

      Close_pair(Px,Py)
        将Px左边加入Lx，Px右边加入Rx  //O(n)
         将Py根据横坐标加入Ly或Ry        //O(n)
         (L1,L2) ← Close_pair(Lx,Ly)    // T(n/2)
         (R1,R2) ← Close_pair(Rx,Ry)   // T(n/2)
         δ ← min(d(L1,L2)，d(R1,R2))     
         对于Py中每个点，如果其距离分割线的距离小于δ，将其加入Ay  //O(n)
         对于Ay中的每个点计算其与后续7个点的距离，如果距离小于δ则更新δ和最近点对。
         return 最近点对