来一篇简单易懂的良心题解。
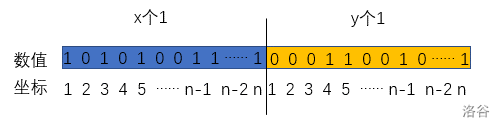
由于数值不是 \(0\) 就是 \(1\),我们可以考虑将逆序对的统计方式化简。
以左区间为例,设 \(x\) 为 \(1\) 的个数,\(p_i\) 为第 \(i\) 个 \(1\) 的坐标,则逆序对个数为 \(\sum\limits_{i=1}^{x}n-p_i-(x-i)\)。也就是 \((n-x)\cdot x+\frac{x\cdot (x+1)}{2}-\sum\limits_{i=1}^{x}p_i\)。
右区间同理。
题目要求两个区间的逆序对个数相同,所以我们把两个式子联立起来。
\((n-x)\cdot x+\frac{x\cdot (x+1)}{2}-\sum\limits_{i=1}^{x}p_i=(n-y)\cdot y+\frac{y\cdot (y+1)}{2}-\sum\limits_{i=1}^{y}p2_i\)
令 \(val(d)=(n-d)\cdot d+\frac{d\cdot (d+1)}{2}\)。
则 \(\sum\limits_{i=1}^{x}p_i-\sum\limits_{i=1}^{y}p2_i=val(x)-val(y)\)。
现在考虑怎么把 \(t\) 个 \(1\) 从左区间移动到右区间。(右到左同理)
我们可以把左区间最右边的 \(t\) 个 \(1\) 移到左区间最靠右的 \(t\) 个位置,再把右区间最左边的 \(t\) 个 \(0\) 移到右区间最靠左的 \(t\) 个位置,接着再用 \(t^2\) 次交换调换 \(01\) 的位置即可。
而将若干个 \(0\) 或 \(1\) 移到某一端的交换次数可以通过预处理 \(O(1)\) 计算出来。
定义 \(sl0_i\) 表示左区间最靠右的 \(i\) 个 \(0\) 的坐标之和,\(sr0_i\) 表示右区间最靠左的 \(i\) 个 \(0\) 的坐标之和。(\(sl1_i\) 和 \(sr1_i\) 同理)
接下来我们枚举完成所有交换操作后左区间 \(1\) 的个数 \(x'\),然后调整若干个 \(1\) 所在的区间,再在区间内进行微调使两边 \(1\) 的坐标的差值符合要求。
令 \(c=|x-x'|\)。
如果 \(x'<x\),则交换次数为
\(\frac{(n - c + 1 + n) \cdot c}{2} - sl1_c + sr0_c - \frac{c \cdot (c + 1)}{2} + c^2 + |sl1_x - sl1_c - sr1_y - sr0_c - val(x') + val(y + c)|\)
否则,交换次数为
\(\frac{(n - c + 1 + n) \cdot c}{2} - sl0_c + sr1_c - \frac{c \cdot (c + 1)}{2} + c ^ 2 + |sl1_x + sl0_c - sr1_y + sr1_c - val(x') + val(y - c)|\)
最后取个最小值就行了。
code
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 1e5 + 5;
ll n, a[N], b[N], x = 0, y = 0, sl0[N], sl1[N], sr0[N], sr1[N], minn = 1e9, tot;
int val(int d) {return (n - d) * d + d * (d + 1) / 2;}
int main() {
ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
cin >> n;
for (int i = 1; i <= n; ++i) {cin >> a[i]; if (a[i]) ++x;}
for (int i = 1; i <= n; ++i) {cin >> b[i]; if (b[i]) ++y;}
tot = 0; for (int i = n; i >= 1; --i) {if (!a[i]) sl0[tot + 1] = sl0[tot] + i, ++tot;}
tot = 0; for (int i = 1; i <= n; ++i) {if (!b[i]) sr0[tot + 1] = sr0[tot] + i, ++tot;}
tot = 0; for (int i = n; i >= 1; --i) {if (a[i]) sl1[tot + 1] = sl1[tot] + i, ++tot;}
tot = 0; for (int i = 1; i <= n; ++i) {if (b[i]) sr1[tot + 1] = sr1[tot] + i, ++tot;}
for (int xx = 0; xx <= x + y; ++xx) {
if (xx > n || x + y - xx > n) continue;
ll c, num;
if (xx < x) {
c = x - xx;
num = (n - c + 1 + n) * c / 2 - sl1[c] + sr0[c] - c * (c + 1) / 2 + c * c + abs(sl1[x] - sl1[c] - sr1[y] - sr0[c] - val(xx) + val(y + c));
} else {
c = xx - x;
num = (n - c + 1 + n) * c / 2 - sl0[c] + sr1[c] - c * (c + 1) / 2 + c * c + abs(sl1[x] + sl0[c] - sr1[y] + sr1[c] - val(xx) + val(y - c));
}
minn = min(minn, num);
}
cout << minn << endl;
return 0;
}
这么良心的题解,点个赞再走吧 QWQ