两道(以我现在的菜狗水平来看)爆算题,没啥感情,全是爆算。

\(M(x,y)\),有 \(|MF_2|=|F_1F_2|=2c=e_2x-a_2=a_1-e_1x\)。
套路:离心率是比值,所以只需要将 \(a,b,c\) 某个值代入特殊值进行计算(最好能算得更简单一点)。
代入 \(a_2=1\),那么 \(c=e_2,e_1=\frac{c}{a_1}\),联立一下得到 \(\frac{e_2}{e_1}-e_1(2+\frac{1}{e_2})-2e_2=0\)
观点:题目里的条件都用到了,那么它应该可以解出来?
两边同时 \(\times e_1\) 并整理得到 \((\frac{1}{e_2}+2)e_1^2+2e_2e_1-e_2=0\),\(\Delta=4e_2^2+4(\frac{1}{e_2}+2)e_2=(2e_2+2)^2\),于是直接二次函数求根公式算出来 \(e_1=\frac{-2e_2+2e_2+2}{\frac{2}{e_2}+4}=\frac{e_2}{1+2e_2}\),其中 \(e_2\in [\frac{3}{2},4]\),于是很容易计算出 \(e_1\in [\frac{9}{4},\frac{8}{3}]\)。

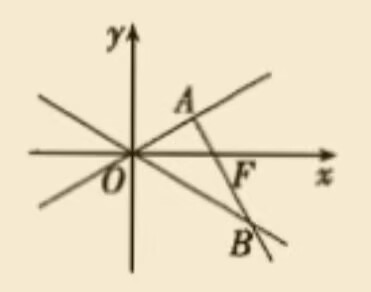
来算一下 \(\tan \angle AOB=\tan(2\angle AOF)=\frac{2ab}{a^2-b^2}\),同时由于 \(AO=a,AB=b+c\),所以 \(\frac{2ab}{a^2-b^2}=\frac{b+c}{a}\),整理得到 \(a^2b-a^2c+b^3+b^c=0\),与 \(a^2+b^2=c^2\) 联立求解。
由于只有 \(a\) 仅出现二次幂,所以代入 \(a^2=c^2-b^2\) 得到 \(bc^2-c^3+2b^2c=0\),这是齐次的,所以约去一个 \(c\) 再除以 \(b^2\) 得到 \(\frac{c}{b}-\frac{c^2}{b^2}+2=0\),令 \(t=\frac{c}{b}\) 即 \(t^2-t-2=0\) 解得 \(t=2\),也就是 \(b:c=1:2\),于是 \(a:b:c=\sqrt 3:1:2\),故离心率为 \(\frac{2\sqrt 3}{3}\)。
这里的思考观察到了式子是齐次的。