在 nfls 的最后一天,来记录一些似乎有意义的题吧。
没有原题(或者我忘了原题)的就简要写下题意,不放原题面了。
- T2 (CF1329E Dreamoon Loves AA)
- T1 (CF1184D2 Parallel Universes (Hard))
- T3 (CF1434E A Convex Game)
- T1 怪兽 (树上 Monster Hunting)
- T2 切割
- T3 导弹
- T1 (CF1023G Pisces)
- T2 (P9312 EGOI2021 Lanterns / 灯笼)
- T3 (CF1662J Training Camp)
- T2 (HDU6815 Funny String)
- T1 冒泡排序
- T3 (P8861 线段)
- T1 最小割树 (HDU6350)
- T2 (HDU6358 Innocence)
- T3 高维碎块 (HDU6355)
- T1 请你自重 (HDU6417)
- T2 猜猜你的 (CF868G)
- T2 自动化leetcode (Gym103104K)
- T2 红心大战
- T1 Path of Sunset
- T2 夏影
- T3 Planetarian
- T2 直线距离
- T2 雪豹失联 (CF500G New Year Running)
- T3 寻找雪豹 (CF1621H Trains and Airplanes)
- T2 sxnlmscp
- T1 情商修炼手册
- T3 数列
- T2 取出排列
- T3 序列 (P7722 [Ynoi2007] tmpq)
- T2 棋盘
- T1 颜色
- T2 字符串
- T2 原神怎么你了!(CF924F Minimal Subset Difference)

在 nfls 打的第一场模拟赛,这场正好与南大营时间撞上,所以打的人不多。而且可以看到在 nfls 进前 50% 是掉分的(
T1 T3 意义不大,写下 T2。
T2 (CF1329E Dreamoon Loves AA)
首先我们肯定不在乎具体的序列了,我们直接将每两个相邻的 \(\mathtt{A}\) 的距离直接写出来。发现,每次操作相当于把一个数分成两个加和与原来相等的数。
考虑什么时候一个 \([L, R]\) 合法。显然对于每一段,肯定是平均分更优,我们考虑每一段被分的次数,一定属于 \(\left[\left\lceil\dfrac{a_i}{R}\right\rceil - 1, \left\lfloor\dfrac{a_i}{L}\right\rfloor - 1\right]\) 这段区间。设一共有 \(m\) 个数,那么一个 \([L, R]\) 满足的条件就是:
- \(\forall i \in [1, m], \left\lceil\dfrac{a_i}{R}\right\rceil \le \left\lfloor\dfrac{a_i}{L}\right\rfloor\);
- \(-m + \displaystyle \sum \left\lceil\dfrac{a_i}{R}\right\rceil \le k \le -m + \sum \left\lfloor\dfrac{a_i}{L}\right\rfloor\)。
容易发现,若我们要满足第二个条件,\(L\) 存在一个最大值,\(R\) 存在一个最小值,可以直接二分得出。我们记作 \(L_0, R_0\)。
- 若 \(L_0 \ge R_0\),那么答案一定为 \(0\),因为我们一定能够任意选择一个 \(x \in [R_0, L_0]\),使得 \(L=R=x\) 成立。第二个条件显然成立,第一个条件由于 \(\left\lceil\dfrac{a_i}{R}\right\rceil \ge \left\lfloor\dfrac{a_i}{L}\right\rfloor\),且根据第二个条件能得出 \(\displaystyle \sum \left\lceil\dfrac{a_i}{R}\right\rceil \le \sum \left\lfloor\dfrac{a_i}{L}\right\rfloor\),所以可以得出 \(\left\lceil\dfrac{a_i}{R}\right\rceil = \left\lfloor\dfrac{a_i}{L}\right\rfloor\),所以一定合法。
- 若 \(L_0 < R_0\),那么一定有 \(\dfrac{a_i}{R} < \dfrac{a_i}{L}\),则 \(\left\lceil\dfrac{a_i}{R}\right\rceil - \left\lfloor\dfrac{a_i}{L}\right\rfloor\) 最大也只可能是 \(1\),而这是唯一一种不满足条件一的情况。那么假如我们现在有若干 \(\left\lceil\dfrac{a_i}{R}\right\rceil - \left\lfloor\dfrac{a_i}{L}\right\rfloor = 1\),我们要对 \(L, R\) 进行一些调整,使它合法。我们容易计算出 \(R\) 增加多少,或 \(L\) 减少多少后,能够使得这个差 \(\le 0\)。那么我们现在相当于有了 \(m\) 条限制 \((x, y)\),形如 \(L \le x\) 或 \(R \ge y\)。这个问题我们只需要排序后,枚举 \(L\) 的值,\(R\) 一维贪心选择即可。

T2 属实没看懂题解,官方题解啥都不证明,比较难蚌埠,遂咕之。
T1 (CF1184D2 Parallel Universes (Hard))
我们有一个非常暴力的 DP,设 \(f_{u, i}\) 表示当前有 \(u\) 个宇宙,当前所在宇宙在第 \(i\) 个,结束期望时间。转移容易写出来,发现带环,可以高斯消元解出,复杂度 \(O(m^6)\)。
考虑减少状态。显然注意到矩阵稀疏,考虑递推系数一类的东西简化方程。具体来讲,我们可以将每一个数表示为 \(f_{u, 2}\) 的线性组合,然后我们再根据 \(f_{u, 2}\) 的转移方程可以列出一个只与 \(f_{u, 2}\) 有关的方程组,直接解这个方程组即可,然后再把要求的 DP 值直接代入求值即可。复杂度 \(O(m^3)\)。
貌似很多人都叫这种方法为主元法?我不知道我在哪里听到的递推系数(
T3 (CF1434E A Convex Game)
我怎么这么多题都没有写题解啊。草。
首先我们肯定要求 SG 函数,要不然 \(n\) 个组合游戏博弈没啥好办法做。我们有一个暴力的 DP \(f_{n, i}\) 表示最后一个选择的是 \(a_n\),上一个选择的数为 \(i\) 的 SG 值,容易枚举下一步选择哪个数做到 \(O(n^3)\) 转移,总的 SG 直就是从每个位置开始的 SG 值的 \(\mathrm{mex}\),然后所有异或起来即可。
考虑优化。首先注意到一件事情,由于要求必须是凸的,那么实际上序列元素最多只有 \(O(\sqrt{n})\) 个。这意味着,SG 值的范围也仅有 \(O(\sqrt{n})\) 个。于是不难想到将 DP 一维与值域互换。我们记录 \(g_{n, x}\) 为最小的 \(i\) 使得 \(f_{n, i} \ge x\),这样我们只对 \(g_{n, x}\) 进行转移。考虑什么情况下可以转移,对于三个数 \(i < j < k\),必须满足 \(a_j - a_i < a_k - a_j\),即 \(a_k > 2a_j - a_i\) 时才能转移,也就是说 \(f_{j, i}\) 仅能由 \(a_k > 2a_j - a_i\) 的 \(f_{k, j}\) 转移来。那么 \(f_{j, i} \ge x\) 相当于对于 \(y \in [0, x)\),都必须存在一个 \(f_{k, j} = y\) 且 \(a_k > 2a_j - a_i\) 的 \(k\)。那么我们记 \(K_{j, y}\) 为最大的 \(k\) 满足 \(f_{k, j} = y\),就有 \(g_{n, x}\) 等于最小的 \(i\) 满足 \(a_i > 2a_j - a_{\min_{y \in [0, x)} K_{j, k}}\),我们只需要再维护出 \(K_{j, y}\) 即可。\(K_{j, y}\) 相当于每次对 \([g_{k, y}, g_{k, y + 1})\) 这段区间与 \(k\) 取 \(\max\),那么我们需要支持区间 \(\max\),单点查询,直接用线段树维护可以做到 \(O(n \sqrt{n} \log n)\)。显然 \(k\) 是单调递减的,所以实际上我们每次是覆盖所有没有被覆盖过的区间,直接拿并查集维护即可 \(O(n \sqrt{n} \ \alpha(n))\)。

把 T2 过了,T1 由于是 APIO2023 讲的题,但是我并没有去,所以成功的签到失败了(
T1 怪兽 (树上 Monster Hunting)
大致题意:你有一棵树,\([2, n]\) 的节点上都有一只怪物,它会对你造成 \(a_i\) 点伤害,你打败它后会回 \(b_i\) 点血。任意时刻血量不能为负数。你需要决定一个打怪物的顺序,使得你存活下来所需血量最少,输出这个血量。你不能经过一个没有被打败的怪兽去打另外一只怪兽。\(n \le 10^5\)。
首先如果没有树的限制,你是可以直接贪心的。对于两只怪兽,容易判断出先打哪只更优。我们根据此可以建立出一个全序关系。那么如果有树,我们倒着去考虑。如果某个节点当前是全序关系中最优的,那么假如这个节点的父亲节点被攻击后,它一定是下一个被攻击的。也就是说,它和父亲节点一定是一起被攻击的。那么我们就可以把两个节点合并在一起。这样,我们用并查集维护,每次将最优的与父亲合并,就能得到最后答案了。
T2 切割
大致题意:给你个字符串,每次询问其子串有多少种切割方式,使得两个串均为回文串。\(n \le 2 \times 10^5\)。
首先有一个经典结论,就是一个串的后缀回文串的长度可以被划分成 \(\log n\) 个等差数列。
那么我们可以直接对前缀与后缀找出这些等差数列,需要用到 PAM,然后每次求两个等差数列中加和等于 \(n\) 的有多少。这是一个二元不定方程的形式,直接 exgcd 求即可。
T3 导弹
大致题意:有 \(n\) 个点在数轴上,坐标分别为 \(a_i\),你从第 \(k\) 个点开始,按某种顺序遍历 \(n\) 个点。你每单位时刻可以走一单位距离。最小化到达每个点的时刻之和。\(n \le 3 \times 10^5, m = \max a_i - \min a_i \le 10^6\)。
首先有一个最暴力的区间 DP,记录当前到达的最左、最右的点与当前的时刻,可以做到 \(O(n^3m)\) 转移。首先记录当前时刻是没有意义的,考虑费用提前计算,我们每走一步就直接将当前没有经过的所有点的贡献提前加上,然后就能做到 \(O(n^2)\) 了。
还能接着费用提前计算。我们先把当前点到每个点的距离全部加上,然后我们每次向右走 \(d\) 距离时,左边没有被经过的所有点的费用都增加了 \(2d\),同理向右走时右边的所有点的距离也都增加了 \(2d\)。于是我们发现,此时向左走与向右走造成的贡献独立开了。那么我们就只需要记录 \(f_i, g_i\) 表示走到了左边第 \(i\) 个,右边第 \(i\) 个时的最小费用,转移类似于 \(f_i = \min\{g_j + 2(a_j - a_i) (n - j)\}\) 一类的东西,发现这个东西是可以斜率优化的,动态维护 \(f_i, g_i\) 的凸壳即可。这个转移的顺序可能比较怪,这是一个类似于最短路的东西,所以我们可以用 Dijkstra 的方法,每次找到左右最小的值进行转移即可。

这题不太想评价。题面写的非常诡异,而且题目难度排序也很诡异。
T1 (CF1023G Pisces)
你管这叫 T1?
首先我们可以根据鱼是否可以相互到达建出一个 DAG,具体来讲就是 \(x < y\) 当且仅当 \(\mathrm{dis}(x, y) < d_2 - d_1\)。那么,我们要求的其实是这个 DAG 的最小链覆盖,根据 Dilworth 定理可以变成求最长反链。
考虑利用树的性质,我们能够得出以下结论:一个集合 \(S\) 为反链,当且仅当:
- 对于当前根的所有子树 \(v\),\(S \cap \mathrm{sub}(v)\) 为反链;
- 存在一个时刻 \(T\),满足 \(S\) 中每个鱼 \((u, d)\),都有 \(|T - d| < \mathrm{dis}(u, root)\)。(即每个点都不能到达根,也不能从根到达这个点)
充分性比较直接,由于 每个子树内都是反链,那么只用考虑子树之间的关系,那么对于两个点 \(u, v\),有 \(\mathrm{dis}(u, v) = \mathrm{dis}(u, root) + \mathrm{dis}(v, root) > |d_u - T| + |d_v - T| \ge |d_u - d_v|\),那么说明这两个点不能互相到达。
必要性证明咕了,感性理解一下(
那么我们可以根据这个来 DP 了。我们设 \(f_{u, T}\) 表示以 \(u\) 为子树,所有点都不能到 \((u, T)\),此时的反链最大多少。对于转移来说,每个子树之间是独立的,那么我们只需要考虑每个子树的贡献即可。先不考虑 \(v\) 上的鱼,那么我们距离根的距离增加了 \(l\),时刻也就可以相应的增加 \(l\),那么贡献就相当于 \(g_{v, T} = \max_{i\in[T - l, T+l]} f_{v, i}\)。此时考虑 \(v\) 上的鱼,它能加入的条件是 \(|T - d| < l\),即 \(d \in (T - l, T + l)\)。发现这个东西恰好与上面的转移范围差一个 \(1\),所以我们可以考虑先将上面转移一个 \(1\),然后将 \(v\) 上的鱼加到对应点值上,然后再转移剩下的 \(l-1\)。
有个问题就是 \(T\) 不一定是整数,但是发现 \(T\) 只能是 0.5 的倍数,所以给 \(T\) 和所有边权都乘 \(2\) 即可。
然后考虑怎么优化这个转移过程。容易发现子树内的 DP 值的数量与子树大小有关系,不难想到维护连续段与树上启发式合并。但是直接维护连续段好像并不好处理 \(\max\) 的转移过程,我们考虑维护差分数组。这样,拓展 \(l\) 位相当于将所有正数向左移动,负数向右移动,若一正一负重叠之后会相互抵消。我们可以拿堆维护每相邻两个正负之间的距离,然后拿 map 维护值,拓展时只需要打标记,然后每次找到距离最小的看是不是相交了,就可以均摊 \(O(\log n)\) 了。
T2 (P9312 EGOI2021 Lanterns / 灯笼)
T3 (CF1662J Training Camp)

这场 T1 恶心到我了,我手推的大 \(\sum\) 式子,然后结果题解说直接插值即可,乐(
T2 T3 都没改,所以这场咕了。

爆炸场,T1 我 \(10^6\) 跑平衡树,正解是线性 ?
T2 T3 两个二合一,属实傻逼,也咕了。
T2 (HDU6815 Funny String)

这场推出来 T1 感觉是我的巅峰了,但是 T2 还是 2 hard 4 me。不过一车人过了 T2,所以还是我菜。
T2 感觉还是很诡异,不写了。
T1 冒泡排序
大致题意:对于一个排列 \(a\),设第 \(i\) 个数左边第一个小于它的数的位置为 \(l_i\),若不存在则为 \(0\);右边第一个小于它的数的位置为 \(r_i\),若不存在等于 \(n+1\)。对于一个排列,设 \(f(a) = \sum_{i=1}^n \min\{i - l_i, r_i - i\}\),求有多少长为 \(n\) 的排列满足 \(f(a) = x\)。多测,\(n \le 300, x \le 10^9, T\le10\)。
首先 \(f(a)\) 这个函数是个很经典的东西,考虑笛卡尔树,那么这个函数实际上等于每个点的左右子树大小的 \(\min\) 的和。而由于这相当于是一个启发式合并的过程,显然 \(f(a)\) 上界是 \(O(n \log n)\) 的。那么我们可以考虑直接对每一种值进行 DP。设 \(f_{n,x}\) 为长度为 \(n\) 的序列且答案为 \(x\) 的方案数,转移不好考虑,所以我们直接从笛卡尔树的角度考虑,枚举左右子树大小,那么也就是 \(f_{n, x} = \sum_{i=0}^{n - 1} \binom{n-1}{i} f_{i, a} f_{n - 1 - i, b} [a + b + \min(i, n - 1 - i) = x]\)。
这玩意直接转移还是极其炸裂。主要是发现第二维的转移非常的丑,我们可以考虑将其写成多项式的形式,这样转移就变成了 \(F_n(x) = \sum_{i=0}^{n - 1} \binom{n - 1}{i} F_i(x) F_{n - 1- i}(x) x^{\min(i, n - 1 - i)}\)。直接维护多项式肯定不成,但是很容易想到我们可以直接插值求这个东西,这样我们就能在 \(O(n^3 \log n)\) 的复杂度内求出所有点值。询问时只需要还原单项系数,这个可以在 \(O(n^2 \log n)\) 的复杂度内计算出,总复杂度 \(O(n^3 \log n + T n^2 \log n)\)。
T3 (P8861 线段)
很强的 ds 题。

不好评价。
T1 最小割树 (HDU6350)
大致题意:给你个仙人掌,求两点之间最大流。
直接建最小割树即可,结束了。
考虑一个环上的最小割,我们肯定会割掉两条边。而容易发现,其中一条一定是这个环上的边权最小的边,那么我们直接把每个环上的最小边权删掉,然后加在环上其它边上。然后就变成一棵树了,剩下的随便做了。
T2 (HDU6358 Innocence)
正解是一个 DP 容斥 矩阵快速幂 balabala 的东西,但是我们有大力 FWT 做法(
然后考场上没推完 :<
T3 高维碎块 (HDU6355)
啥啥啥,广为人知?这是啥?
首先题目是最小链覆盖,转成最长反链。然后据说是广为人知的 Sperner 定理 的推广,我没听说过,搜了也没看懂。呃呃。
反正大概是能通过猜测得出,二维情况下选对角线最优,那么高维情况下选所有坐标之和等于 \(M\),且 \(M\) 是中点的坐标之和最优,大概就是 \(M = \left \lfloor \frac{\sum_{i = 1}^{n}(p_i + 1)}{2} \right \rfloor\)。
证明复制一个。
下证答案上界为权值为 \(M\) 的点数,只需构造一组方案使得链数为 \(M\)。若一条链满足起始位置与终止位置之和为 \(\sum_{i = 1}^{n} (p_i + 1)\),则将其称为对称链。由于链上的点权值连续,所以一条对称链上必然有一个权值为 \(M\) 的点。下证可以构造一组方案,使得两两不交的对称链覆盖所有点。
记 \((x_1, x_2, \ldots, x_{n - 1}) + x_n = (x_1, x_2, \ldots, x_{n - 1}, x_n)\)。
考虑归纳证明。\(n = 1\) 时,结论显然成立。
当 \(n > 1\) 时,若 \(n - 1\) 满足,则取出 \(n - 1\) 维的对称链 \(u_1 \to u_2 \to \cdots \to u_k\),构造如下几条链:
\[\begin{matrix} u_1 + 1 \to u_2 + 1 \to \cdots \to u_k + 1 \to u_k + 2 \to \cdots \to u_k + p_n \\ u_1 + 2 \to u_2 + 2 \to \cdots \to u_{k - 1} + 2 \to u_{k - 1} + 3 \to \cdots \to u_{k - 1} + p_n \\ \cdots \\ u_1 + \min(k, p_n) \to \cdots \to u_{k + 1 - \min(k, p_n)} + \min(k, p_n) \to \cdots \to u_{k + 1 - \min(k, p_n)} + p_n \end{matrix} \]不难发现,这样的链是 \(n\) 维的对称链,且两两不交地覆盖了所有点,故链数可以为 \(M\)。\(\square\)
然后就是个经典东西,求所有 \(x_i \in [1, a_i], \sum x_i = M\) 的 \(x_i\) 数。这相当于是一个有上限的小球放盒子的东西,可以容斥去做。但是直接容斥是 \(O(2^n)\),寄了。\(n \le 32\),考虑 meet in the middle,组合数可以用范德蒙德卷积拆开,然后就能合并了,复杂度好像是个 \(O(n^2 2^{\frac{n}{2}})\) 之类的。我没写,口胡的。

可以看到,排名不断创历史新高!
这场 T1 给我恶心到了。然后我赛后发现 jjdw 已经完全探究过这个问题了。只能说太恐怖了。
然后 T2 还是个类欧题,呃呃。不过趁此学习了下万欧,感觉很厉害,不过应该还是没啥用。
T3 好像是个什么分块 ds 题,没看,咕。
T1 请你自重 (HDU6417)
大致题意:给你 \(n\) 个点的无向完全图,\(i, j\) 之间的边权为最小的 \(k\) 使得 \(ijk\) 为完全平方数。设 \(d(i, j)\) 为 \(i,j\) 之前的最短路,求 \(\sum_{i \le j} d(i, j)\)。\(n \le 10^{10}\)。
首先第一件事情,我们把 \(i, j\) 质因子分解,那么不难发现最短路一定是每次改变 \(i\) 个一个质因子,因为乘法永远比加法大。那么 \(d(i, j)\) 实际上等于所有指数为奇数的质因子之和。另外,如果 \(ij\) 已经是完全平方数,则还需要有额外的 \(1\) 的贡献。由于贡献是加法,容易想到单独考虑每一个质因子的答案。考虑如何计算指数恰好为 \(i\) 的个数,容易容斥得到 \(\left\lfloor\dfrac{n}{p^i}\right\rfloor - \left\lfloor\dfrac{n}{p^{i + 1}}\right\rfloor\)。那么设 \(f(n,p)\) 为 \(p\) 的指数为偶数的数的个数,那么有 \(f(n, p) = \displaystyle \sum_{i\ge 0} (-1)^i \left\lfloor\dfrac{n}{p^i}\right\rfloor\)。答案即为 \(\sum_{p \in \mathrm{prime}} f(n, p) (n - f(n, p))\)。
容易想到根号分治,对于小于等于 \(\sqrt{n}\) 的 \(p\) 来说,这个式子显然可以暴力计算;对于大于 \(\sqrt{n}\) 的 \(p\) 来说,\(f(n, p) = \left\lfloor\dfrac{n}{p}\right\rfloor\),于是式子实际上就变成了 \(\displaystyle \sum_{p \in \mathrm{prime}} \left\lfloor\dfrac{n}{p}\right\rfloor \left(n - \left\lfloor\dfrac{n}{p}\right\rfloor\right)\)。这个东西容易整除分块加一个 min_25 筛求出。
但是还有一件事情,那就是还有权值为 \(1\) 的。我们需要计算 \(\sum_{i=1}^n \sum_{j=1}^n [ij \textsf{ 是完全平方数}]\)。类似于上面的思路,我们考虑枚举 \(i, j\) 中指数为奇数的质因子,把这些除去之后只需要 \(i, j\) 均为完全平方数即可。这等价于 \(\sum_{i=1}^n \mu^2(i) \left\lfloor\sqrt{\frac{n}{i}}\right\rfloor\)。那么,只需要一个整除分块再加上 \(\mu^2\) 前缀和即可。这个问题可以看 jijidawang 的博,比我研究的透彻,拜谢 jjdw。总之最简单的办法就是用单次 \(O(\sqrt{n})\) 的算法加上预处理前 \(O(n^\frac{2}{3})\) 项会跑的很快。
你管这叫 T1?
T2 猜猜你的 (CF868G)

掉分掉到底了属于是(
T1 弱智题,检验会不会写低于根号的素性测试?
T2 是个数据结构,罕见的场上写出来了。但是 T1 挂了 40 分,喜提 32 名。要不然就第九了,呃呃。
T3 是个图论 DFS 树上分类讨论,好像巨麻烦,咕。
T2 自动化leetcode (Gym103104K)
有一个 polylog 的做法,不过太复杂我们直接扔掉。
直接考虑分块,对每个块预处理出位置映射。发现每次操作会把区间划分成两个一次函数。直接维护函数并不容易,但是我们发现此时只有一端是有用的,另一端永远都与它相等,所以我们可以拿并查集将相等的位置缩起来,这样我们只需要维护这个一次函数即可。我们每次只缩较小的一边,这样均摊复杂度就是对的。这部分比较类似第二分块。然后就做完了。

这场只能说离谱。
T1 真的不好评价,大概就是个暴力写出 GF 然后暴力分式分解然后暴力扩域特征根解递推式,加上一堆特判的鬼题。
T2 没调完,感觉很难写,咕了,口胡一下。
T3 类喵了个喵构造题,没改,另外附有:
T2 红心大战
大致题意:给定数轴上 \(n\) 个点,设 \(f(x, l, r)\) 为,从 \(x\) 开始,每次走到距离当前点最近的没有经过的点,距离相等走左边,经过所有 \([l, r]\) 内的点经过的距离。多次询问,每次查询 \(\sum_{i=l}^r f(i, l, r)\)。
首先有一个关键结论:从一个点开始,经过所有点只会转向 \(O(\log n)\) 次。这个是很容易发现的,因为如果某一时刻,走到 \(r\) 要转向去 \(l-1\) 时,必须满足 \(a_{r + 1} - a_r \ge a_r - a_{l - 1}\),那么容易发现每出现这样的情况,整个区间的长度一定会增加一倍,那么就只会转向 \(O(\log n)\) 次。可以大概画画,懒得仔细证了。
那么,我们就可以预处理出来从每个点开始,经过的路径。考虑出现了 \([l, r]\) 的限制会怎样,从某个点开始前面走的步实际上是不变的,当第一次路径穿过 \(l/ r\) 时,下一步一定就是从 \(r \to l\) 或 \(l \to r\) 了。那么我们可以将每一步的贡献拆开,考虑每一步会给哪些区间造成贡献。大概会分成三类,一种是完全包含在区间内的,一种是撞到右边界的,一种是撞到左边界的。这几种情况造成的贡献都是一个矩形,我们可以直接离线下来后扫描线做这个东西。
复杂度大概是两个 \(\log\)。

再创历史新高!
T1 可见我的 ds 基础不牢,做法想到了但是不会维护,乐。
T2 倒还挺强的。
T3 可能也可能,但是我没改,所以口胡。
T1 Path of Sunset
大致题意:给你一个长为 \(n\) 的序列,每次选择一个长度为 \(k\) 的连续段,删除其中的最小值,一共进行 \(m\) 次操作。定义权值为删除的数的最大值减最小值,最小化权值。\(n \le 10^6\)。
考虑直接枚举最小值,那么我们现在的目的就是要求最大值最小。由于我们已经枚举了最小值,那么比这个值更小的数就都不能被删除,而又由于我们每次删除的是最小值,那么我们选择的区间内就不能出现小于当前最小值的数。那么我们相当于用这些数将序列划分成了若干段,每一段有一个取数的上限(\(\textsf{区间长度}- k+1\)),取全体前 \(m\) 小的数。
然后我们考虑动态的维护这个东西,考虑从大到小去枚举这个,这样每次相当于会将若干个位置的左右两个区间拼接起来。拼接起来之后,不能选的数会减少。我们可以用可并堆维护这个东西,每个区间维护两个堆,表示可以选的与不能被选的,不能被选的里面有最多 \(k-1\) 个数。每次合并后,将多余 \(k-1\) 个数加入可以选的堆里。然后每次选所有堆中的前 \(m\) 小,这个同样可以拿堆去维护,只保留前 \(m\) 大即可。
T2 夏影
大致题意:给定一棵树,每个点上有一个物品,价格为 \(b_i\),权值为 \(a_i\),每个物品只能购买一个,且树上相邻的两个物品不能同时购买。对于每一个 \(m \in [1, M]\),求出在恰好花费 \(m\) 的价格后,最大权值。\(n \le 100, m \le 4000\)。
首先有一个很显然的树形背包做法,容易做到 \(O(nm^2)\)。涉及到合并两个背包,就基本上做不到更优了。树形背包存在不合并背包的 \(O(nm)\) 的做法,将问题拍到 dfs 序上,这样只需要考虑每次拓展一个物品,复杂度就优秀了。但是并不能直接应用在本题上,因为题目要求独立集,不能直接拍到 dfs 序列上去。但是我们仍然能够利用类似的思想去做。显然有一个直接状压的做法,但是注意到我们并不需要记录所有点的选择情况,只需要记录一部分。那么我们有两种做法:
- 点分树:我们可以建出点分树,只记录当前点到根的点的选择方案,由于在当前分治中心中,我们能碰到的非当前分治区域内的点一定都是当前点到根的这些点,所以仅需要记录这些点的选择方案即可。而点到根的点数为严格 \(\log n\),于是我们就有了 \(O(2^{\log n} nm) = O(n^2m)\) 复杂度的做法。
- 树链剖分:考虑直接 dfs 记录点到根的选择方案,此时如果我们只记录轻边链接的父亲节点的选择方案,复杂度和上述就一致了。具体来说就是我们优先递归轻儿子,轻儿子都处理完后再去走重儿子,这样我们是不需要记录重儿子的父亲选择方案的,因为已经没有点与它相邻了。
T3 Planetarian
大致题意:定义 \(f(s)\) 为字符串 \(s\) 中出现次数大于 \(1\) 的最长的子串的长度。给定数组 \(a\) 与一个字符串 \(s\),定义 \(s\) 的一个子串的权值为这个子串的每个下标对应的 \(a\) 的最大值。\(q\) 次询问,每次询问 \(s[l, r]\) 的所有子串 \(s'\) 中,满足 \(f(s') \ge t\) 的最小权值。\(n, q \le 10^5\)。
首先发现一件事情,有用的 \(s\) 串当且仅当存在出现次数大于 \(1\) 的最长子串为这个串的后缀。如果不是后缀,那么把后面的字符删掉一定不劣。而第二件事情,对于同一个串来说,能造成贡献的一定是相邻的两次出现位置。如果不相邻,同样可以缩短字符串使得答案不变且不劣。
那么实际上能造成贡献的位置对,就是所有子串的 endpos 集合中的相邻位置。而这样的相邻位置只有 \(O(n \log n)\) 个,容易通过建 SAM 时对 endpos 集合进行启发式合并得到。那么此时,我们就仅有 \(O(n \log n)\) 对位置需要考虑了。
考虑一对 \((x, y)\),这两个前缀的最长公共后缀长为 \(p\),那么假如询问区间为 \([l, r]\),这个位置对的最大可能长度就是 \(\min(p, x - l + 1)\)。那么,只要 \(\min(p, x - l + 1) \ge t\),这个位置对就能对答案造成贡献。这个东西是可以用主席树维护的,这样就能做到动态求单个 \(f(l, r)\) 了。
考虑 \(a\) 的限制,首先容易单调栈求出对于每一个 \(a_i\),\([l, r]\) 内的区间最大值为 \(a_i\)。然后我们考虑这些 \([l, r]\) 与当前询问区间的关系,完全包含或贴左/右边。
先考虑完全包含,我们只需要考虑 \(f(l, r)\) 即可,这个根据上面的结论我们可以直接快速求出一个 \(f(l, r)\) 的值,是一个类似于三维偏序的东西。
然后考虑贴边的情况。我们二分一个 \(a\),找到合法的这些 \(a\) 内 \(r\) 的最大值,然后看 \(f(L, \max r)\) 是否 \(\ge t\),这样我们就能找到最大的 \(a\) 了。当然理论来说只有 \(i \ge L\) 的 \([l_i, r_i]\) 能够造成贡献,但是如果存在 \(i < L\) 的情况,我们可以取 \((i, r_i]\) 内的最大值,这个区间一定也与询问区间有交,这样最后的最大值一定不会是 \(i < L\) 的情况。

继续垫底!
泰裤辣!
这场打吐了,但是还得交点什么东西,于是就交一个暴力跑路,成功垫底?♂️
T1 是个很恶心的树形 DP,不写了就。
T2 还是很有意思的。
T3 又是一个 DFS 树上分类讨论题,没写,咕咕。
T2 直线距离
大致题意:给定平面上 \(n\) 个整点,两两连线,能够得到 \(\dfrac{n(n-1)}{2}\) 条直线。求 \((0, 0)\) 到这些直线中第 \(k\) 小的距离。\(n \le 10^5\)。
首先肯定是二分答案,那么就是考虑有多少直线到点的距离小于等于 \(d\)。发现这相当于求圆心为 \((0, 0)\),半径为 \(d\) 的圆与多少直线有交。
这个圆与直线有交还是比较抽象。考虑两个点之间的连线什么情况下与圆有交。有一个很巧妙的做法(也许算是套路?),我们把点映射到圆上的一段圆弧,考虑圆弧之间的关系。这道题我们考虑每个点到圆的两条切线,将两个切点直接的圆弧拉出来。发现,两个点的连线与圆不相交,当且仅当两条对应的圆弧交叉但不包含。
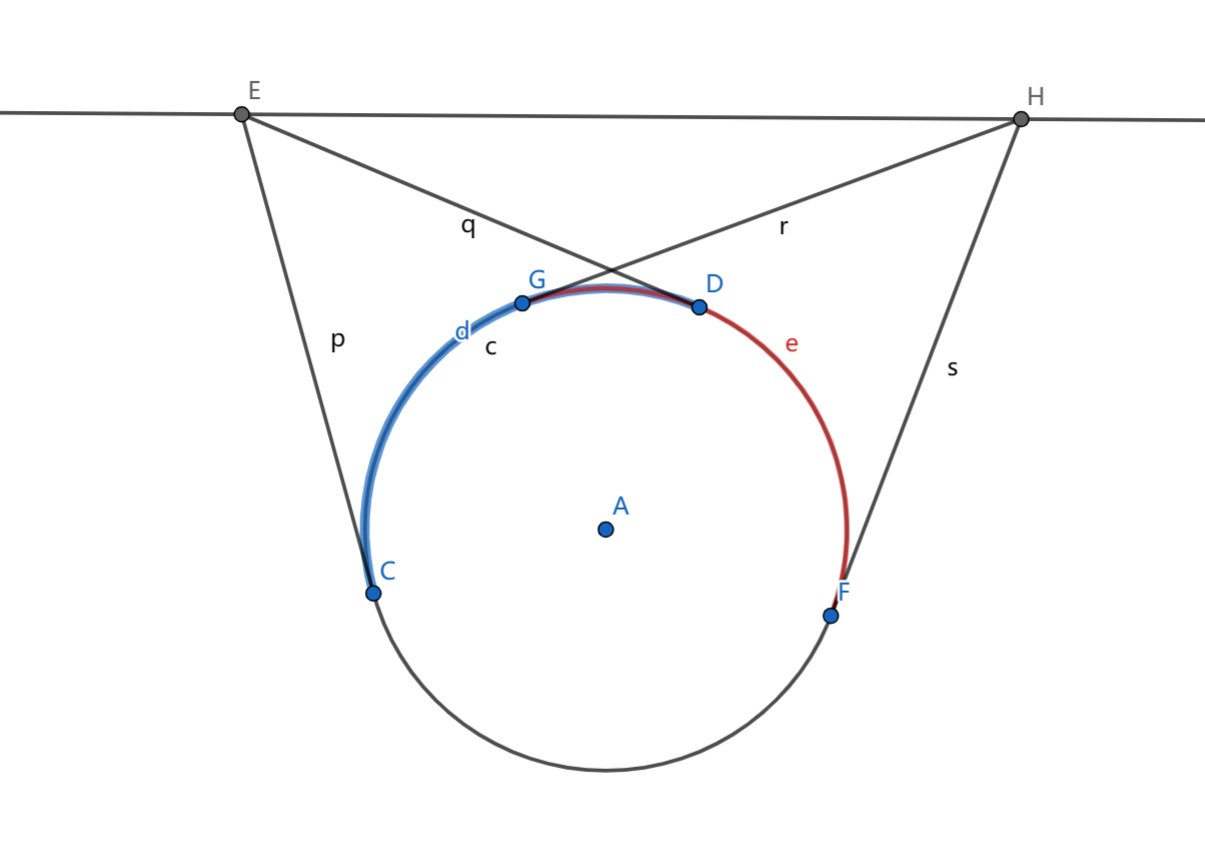
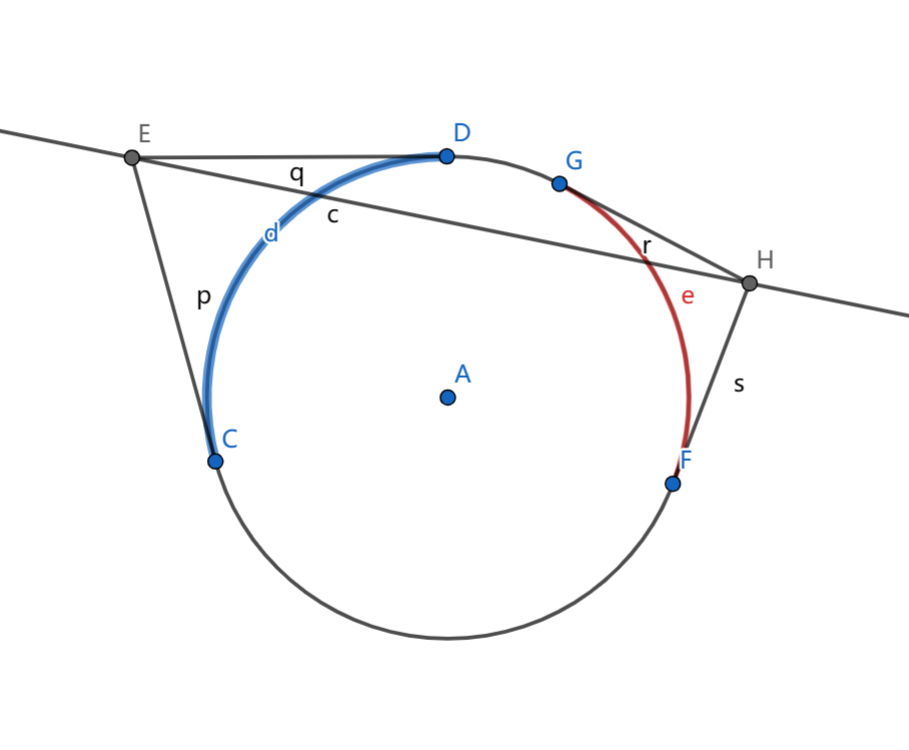
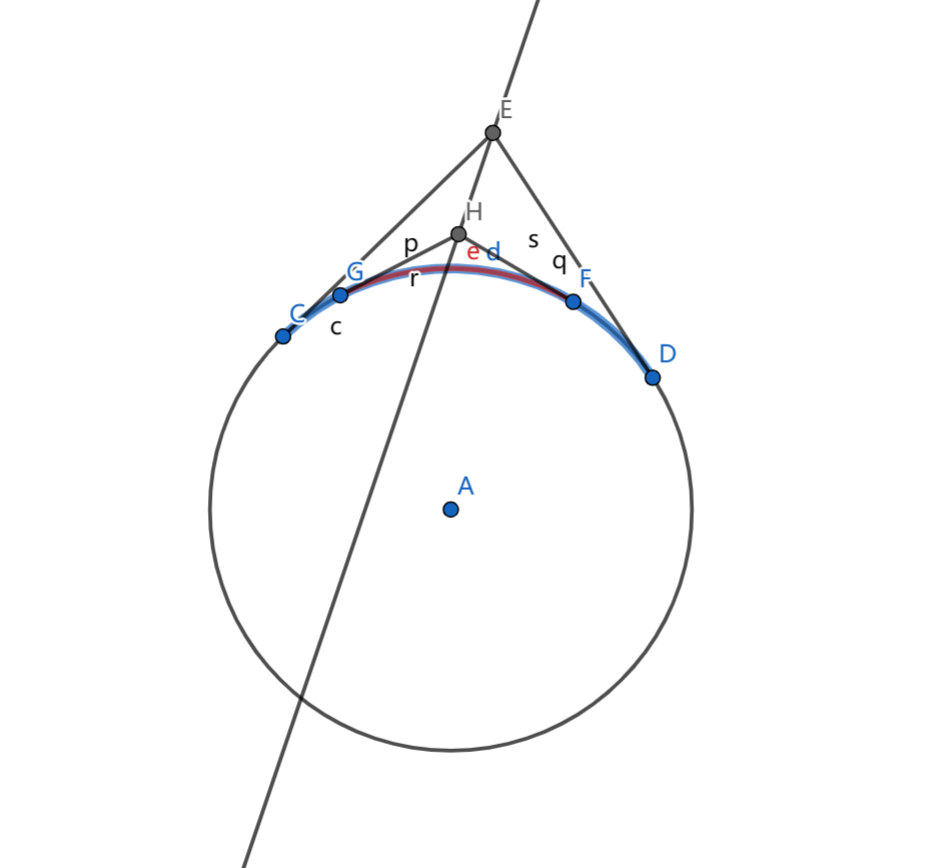
那么我们就可以直接把每个点全部转化成区间,然后从某一点把环断开即可。容易发现两段圆弧是没有区别的,所以可以直接断。然后离散化之后,就是一个很简单的问题了,求有多少区间相交,容易树状数组求出答案。

T1 是个很简单的题,然后 T2 类欧调了一场没调出来,乐死了。
T2 雪豹失联 (CF500G New Year Running)
我的做法比较阴间一点,直接推类欧 / 万欧应该会比这个简单的多(
T3 寻找雪豹 (CF1621H Trains and Airplanes)
首先容易有一个简单的贪心,考虑从一个点开始到根每个区域 \(i\) 经过了 \(c_i\) 次,那么答案就是 \(\sum \min\{p_i, c_i \times f_i\}\)。那么我们就只关心每个点被经过了多少次。
接下来我们又可以发现,每个区域被经过的次数只有两种可能性,大致是 \(\left\lfloor\dfrac{dep_i - dep_j}{T}\right\rfloor\) 或 \(\left\lceil\dfrac{dep_i - dep_j}{T}\right\rceil\),而这两个东西肯定是在一段区间内为一个值,另一端区间内为另一个值。那么实际上,对于同一个区域的点,\(\{c_i\}\) 这个序列除当前所在区域的次数外,仅有 \(O(k)\) 种可能性。我们可以直接暴力求然后暴力去重,询问时暴力枚举,即可做到 \(O((n + q) k^2)\)。

上分了!太感动了
赛时过了两道题,然后也就没了。
但是这场好像也没啥可写的了。T1 是 GP of Tokyo 的一道题的弱化版(但是数据范围开大,导致看起来很卡常?)
T2 是倍增值域分块板子,虽然有更简单的做法
T3 太诡异了,看不懂,咕。

这场其实不好评价(
T1 是个套路题,求补图最大匹配,做法就是先贪心匹配然后再用并查集维护匈牙利。
T2 是个没有任何难度的五合一题。然后我还被卡常了,呃呃呃。
T3 可能还是有意思的,我也没改,大概就是主席树优化建图。复制一份代码,等我啥时候闲的可以研究下。
#include <iostream>
#include <algorithm>
#include<cmath>
#include<cstring>
#include<cstdio>
#include<cstdlib>
#include<vector>
#include<iomanip>
#include<ctime>
#include<set>
#include<map>
#include<queue>
#include<stack>
#include<bitset>
#include<cassert>
#define sqr(x) ((x)*(x))
#define fz1(i,n) for ((i)=1;(i)<=(n);(i)++)
#define fd1(i,n) for ((i)=(n);(i)>=1;(i)--)
#define fz0g(i,n) for ((i)=0;(i)<=(n);(i)++)
#define fd0g(i,n) for ((i)=(n);(i)>=0;(i)--)
#define fz0k(i,n) for ((i)=0;(i)<(n);(i)++)
#define fd0k(i,n) for ((i)=(((long long)(n))-1);(i)>=0;(i)--)
#define fz(i,x,y) for ((i)=(x);(i)<=(y);(i)++)
#define fd(i,y,x) for ((i)=(y);(i)>=(x);(i)--)
#define fzin fz1(i,n)
#define fzim fz1(i,m)
#define fzjn fz1(j,n)
#define fzjm fz1(j,m)
#define ff(c,itr) for (__typeof((c).begin()) itr=(c).begin();itr!=(c).end();++itr)
#define pb push_back
#define mk make_pair
#define rdst(st,len){static char ss[len];scanf(" %s",ss);(st)=ss;}
#define spln(i,n) (i==n?'\n':' ')
#define fac_init(n){fac[0]=fac[1]=inv[1]=fi[0]=fi[1]=1;fz(i,2,n){fac[i]=1ll*fac[i-1]*i%mod;inv[i]=1ll*(mod-mod/i)*inv[mod%i]%mod;fi[i]=1ll*fi[i-1]*inv[i]%mod;}}
using namespace std;
typedef long long i64;
typedef long double f80;
typedef unsigned int u32;
typedef unsigned long long u64;
//typedef __int128 i128;
//typedef unsigned __int128 u128;
/*#ifndef ONLINE_JUDGE
FILE *___=freopen(".in","r",stdin);
#endif*/
inline void read(int &x)
{
char c;int f=1;
while(!isdigit(c=getchar()))if(c=='-')f=-1;
x=(c&15);while(isdigit(c=getchar()))x=(x<<1)+(x<<3)+(c&15);
x*=f;
}
int hd[48000005],nxt[96000005],to[96000005],cnt,tot,vis[48000005];
void link(int x,int y){if(!x||!y)return;/*cerr<<x<<' '<<y<<endl;*/tot++;nxt[tot]=hd[x];to[tot]=y;hd[x]=tot;}
int nwv(){cnt++;vis[cnt]=hd[cnt]=0;return cnt;}
bool flg;
void dfs(int x)
{
vis[x]=1;int i;
for(i=hd[x];i;i=nxt[i]){
if(!vis[to[i]])dfs(to[i]);
else if(vis[to[i]]==1) flg=1;
}
vis[x]=2;
}
struct seg0
{
int tag[2400005],hv[2400005];
void build(int x,int l,int r)
{
tag[x]=hv[x]=0;if(l==r)return;int mid=(l+r)/2;
build(x+x,l,mid);build(x+x+1,mid+1,r);
}
void update(int x,int l,int r,int ql,int qr,int c)
{
if(ql<=l&&r<=qr){tag[x]=hv[x]=c;return;}int mid=(l+r)/2;
if(ql<=mid)update(x+x,l,mid,ql,qr,c);if(qr>mid)update(x+x+1,mid+1,r,ql,qr,c);
hv[x]=(tag[x]|hv[x+x]|hv[x+x+1]);
}
bool query(int x,int l,int r,int ql,int qr)
{
if(ql<=l&&r<=qr) return hv[x];if(tag[x]) return 1;int mid=(l+r)/2;
if(ql<=mid&&query(x+x,l,mid,ql,qr))return 1;
if(qr>mid&&query(x+x+1,mid+1,r,ql,qr))return 1;
return 0;
}
}tr0;
struct seg1
{
int rt,cnt,lc[24000005],rc[24000005],tag[24000005],val[24000005];
void init(){rt=cnt=0;}
int nwnd(int x){cnt++;lc[cnt]=lc[x];rc[cnt]=rc[x];tag[cnt]=tag[x];val[cnt]=val[x];return cnt;}
void pushup(int x)
{
if(!val[lc[x]]) val[x]=val[rc[x]];
else if(!val[rc[x]]) val[x]=val[lc[x]];
else if(val[lc[x]]==val[rc[x]]) val[x]=val[lc[x]];
else{val[x]=nwv();link(val[x],val[lc[x]]);link(val[x],val[rc[x]]);}
}
void update(int &x,int l,int r,int ql,int qr,int c)
{
x=nwnd(x);if(ql<=l&&r<=qr){tag[x]=val[x]=c;return;}int mid=(l+r)/2;assert(!tag[x]);
if(ql<=mid)update(lc[x],l,mid,ql,qr,c);if(qr>mid)update(rc[x],mid+1,r,ql,qr,c);
pushup(x);
}
void rglink(int x,int l,int r,int ql,int qr,int c)
{
if(ql>qr||!val[x])return;if(tag[x]){link(c,tag[x]);return;}
if(ql<=l&&r<=qr){link(c,val[x]);return;}int mid=(l+r)/2;
if(ql<=mid)rglink(lc[x],l,mid,ql,qr,c);
if(qr>mid)rglink(rc[x],mid+1,r,ql,qr,c);
}
}tr1;
struct seg2
{
int rt,cnt,lc[24000005],rc[24000005],tag[24000005],val[24000005];
void init(){rt=cnt=0;}
int nwnd(int x){cnt++;lc[cnt]=lc[x];rc[cnt]=rc[x];tag[cnt]=tag[x];val[cnt]=val[x];return cnt;}
void pushup(int x)
{
if(!val[lc[x]]) val[x]=val[rc[x]];
else if(!val[rc[x]]) val[x]=val[lc[x]];
else if(val[lc[x]]==val[rc[x]]) val[x]=val[lc[x]];
else{val[x]=nwv();link(val[lc[x]],val[x]);link(val[rc[x]],val[x]);}
}
void update(int &x,int l,int r,int ql,int qr,int c)
{
x=nwnd(x);if(ql<=l&&r<=qr){tag[x]=val[x]=c;return;}int mid=(l+r)/2;assert(!tag[x]);
if(ql<=mid)update(lc[x],l,mid,ql,qr,c);if(qr>mid)update(rc[x],mid+1,r,ql,qr,c);
pushup(x);
}
void rglink(int x,int l,int r,int ql,int qr,int c)
{
if(ql>qr||!val[x])return;if(tag[x]){link(tag[x],c);return;}
if(ql<=l&&r<=qr){link(val[x],c);return;}int mid=(l+r)/2;
if(ql<=mid)rglink(lc[x],l,mid,ql,qr,c);
if(qr>mid)rglink(rc[x],mid+1,r,ql,qr,c);
}
}tr2;
int n,m,i,j;
struct ii{int xl,xr,yl,yr,id;}a[300005],b[300005];
bool inter(ii a,ii b){return max(a.xl,b.xl)<min(a.xr,b.xr)&&max(a.yl,b.yl)<min(a.yr,b.yr);}
vector<int> allx,ally;
vector<int> vi1[600005],vo1[600005],vi2[600005],vo2[600005];
void solve()
{
read(n);allx.clear();ally.clear();cnt=n;tot=0;fz1(i,n)hd[i]=vis[i]=0;
fz1(i,n){
read(a[i].xl);read(a[i].yl);read(a[i].xr);read(a[i].yr);a[i].xr+=a[i].xl;a[i].yr+=a[i].yl;a[i].id=i;
allx.push_back(a[i].xl);allx.push_back(a[i].xr);ally.push_back(a[i].yl);ally.push_back(a[i].yr);
char dir;while(!isupper(dir=getchar()));b[i]=a[i];
if(dir=='R') b[i].xr=a[i].xr*2-a[i].xl,b[i].xl=a[i].xr;
if(dir=='L') b[i].xl=a[i].xl*2-a[i].xr,b[i].xr=a[i].xl;
if(dir=='D') b[i].yl=a[i].yl*2-a[i].yr,b[i].yr=a[i].yl;
if(dir=='U') b[i].yr=a[i].yr*2-a[i].yl,b[i].yl=a[i].yr;
allx.push_back(b[i].xl);allx.push_back(b[i].xr);ally.push_back(b[i].yl);ally.push_back(b[i].yr);
}
sort(allx.begin(),allx.end());allx.resize(unique(allx.begin(),allx.end())-allx.begin());sort(ally.begin(),ally.end());ally.resize(unique(ally.begin(),ally.end())-ally.begin());
fz1(i,n){
a[i].xl=upper_bound(allx.begin(),allx.end(),a[i].xl)-allx.begin();a[i].xr=upper_bound(allx.begin(),allx.end(),a[i].xr)-allx.begin();
a[i].yl=upper_bound(ally.begin(),ally.end(),a[i].yl)-ally.begin();a[i].yr=upper_bound(ally.begin(),ally.end(),a[i].yr)-ally.begin();
b[i].xl=upper_bound(allx.begin(),allx.end(),b[i].xl)-allx.begin();b[i].xr=upper_bound(allx.begin(),allx.end(),b[i].xr)-allx.begin();
b[i].yl=upper_bound(ally.begin(),ally.end(),b[i].yl)-ally.begin();b[i].yr=upper_bound(ally.begin(),ally.end(),b[i].yr)-ally.begin();
}
fz1(i,allx.size()) vi1[i].clear(),vo1[i].clear(),vi2[i].clear(),vo2[i].clear();
fz1(i,n){
vi1[a[i].xl].push_back(i);vo1[a[i].xr].push_back(i);
vi2[b[i].xl].push_back(i);vo2[b[i].xr].push_back(i);
}
tr0.build(1,1,ally.size());
fz1(i,allx.size()){
ff(vo2[i],it) tr0.update(1,1,ally.size(),b[*it].yl,b[*it].yr-1,0);
ff(vi2[i],it){
if(tr0.query(1,1,ally.size(),b[*it].yl,b[*it].yr-1)){puts("NO");return;}
tr0.update(1,1,ally.size(),b[*it].yl,b[*it].yr-1,1);
}
}
// bf: fz1(i,n)fz1(j,n)if(inter(b[i],a[j])) link(i,j);
tr1.init();tr2.init();
fz1(i,allx.size()){
ff(vo1[i],it) tr1.update(tr1.rt,1,ally.size(),a[*it].yl,a[*it].yr-1,0);
ff(vo2[i],it) tr2.update(tr2.rt,1,ally.size(),b[*it].yl,b[*it].yr-1,0);
ff(vi1[i],it){
tr2.rglink(tr2.rt,1,ally.size(),a[*it].yl,a[*it].yr-1,*it);
tr1.update(tr1.rt,1,ally.size(),a[*it].yl,a[*it].yr-1,*it);
}
ff(vi2[i],it){
tr1.rglink(tr1.rt,1,ally.size(),b[*it].yl,b[*it].yr-1,*it);
tr2.update(tr2.rt,1,ally.size(),b[*it].yl,b[*it].yr-1,*it);
}
}
flg=0;fz1(i,n)if(!vis[i]){dfs(i);if(flg){puts("NO");return;}}
puts("YES");
}
int main()
{
cerr<<(sizeof(hd)*5+sizeof(tr1)*2)/1048576<<endl;
freopen("rect.in","r",stdin);freopen("rect.out","w",stdout);
int t;read(t);while(t--)solve();
return 0;
}

第一次考进前十!(for real,第一场只是因为考的人本来就少所以基本不算)
不过 T1 是找规律找出来的,T2 退火退的,比较生草(
T2 sxnlmscp
大致题意:给定平面上 \(n\) 个整点,第 \(i\) 个点有一个权值 \(v_i\),你需要求出一个半径最小的圆,使得存在一个在圆内的点集权值异或和大于等于 \(m\)。\(n \le 3000\)。
首先显而易见的是,最后的一个圆一定会经过一个点。那么我们可以枚举这个点,然后考虑经过这个点的半径最小的圆。枚举之后考虑二分答案,那么最后的圆的圆心一定在以这个点为圆心的圆上。再考虑所有点什么时候会在这个圆内,发现其在圆内也对应着圆上的一段圆弧,这个也是可以求出来的。那么这样我们就将问题拍到了序列上,接下来只需要写一个带删并查集即可。这样时间复杂度为 \(O(n^2 \log^2 n)\),还是通过不了。
这时候考虑一个类似于求点集最小覆盖圆的方法。我们相当于在找一个序列中的最大值,如果我们随机选一个位置进行检查,只有当这个点的答案可能大于当前的最大值时再二分,这样每次期望会将序列中一半的数删去,这样期望只会对 \(\log n\) 个点进行二分,加上前面 check 的复杂度,总复杂度为 \(O(n^2 \log n + n \log^2 n)\),可以通过。

好似。
T1 由于一个 corner case 没判挂成 10 分,笑死了。
T2 阴间构造,确实是不会,但是好像乱搞能拿巨大多分。我啥都没写。
T3 是个神奇交互,倒是确实不难,但是我脑子彻底寄了,啥都想不到。
T1 情商修炼手册
大致题意:给定一个森林,每个节点有权值,初始所有权值都为 \(0\)。每个点都有一个区间 \([l_i, r_i]\),你可以进行若干次操作,每次将一个子树内的所有权值加 \(v\)(可以是负数)。求最少需要进行多少次操作,使得每个点的权值都属于其对应的区间内。
我做法比较暴力了,但是反正是能过的,不管(
首先发现,我们肯定不会对同一个点进行多次操作,那么我们可以考虑对哪些点进行操作。发现每进行一次操作,我们实际上是将这个点到父亲的边断掉,这样同一连通块内的权值相等。那么我们考虑一个 DP,设 \(f_{u, i}\) 表示 \(u\) 子树内权值为 \(i\) 的最少操作次数,转移形如 \(f_{u,i} = \sum_v \min\{f_{v, i}, f_{v, j} + 1\}\)。容易发现每个点真正有用的 DP 值实际上只有两个,我们可以直接维护连续的 DP 区间。又发现一个子树内的区间个数是 \(O(siz)\) 的,于是我们直接树上启发式合并即可。
存在线段树合并做法,但是我懒得想,因为区间非最大值赋值成某个数这个操作感觉太诡异了,懒得想怎么合并(
T3 数列
大致题意:交互题。交互库有一个序列 \(a_i\),你只知道序列长度 \(n\)。你可以进行两种询问:
- 给定 \(i\),询问 \(a_i\) 的值;
- 给定一个互不相等的下标集合 \(S\),询问 \(\{|a_i - a_j|\,|i, j \in S, i < j\}\)(可重集)。
你需要得到这个序列。\(n \le 250\),最多询问 \(27\) 次。
首先我们有一个重要观察:
- 我们可以在两次询问内找出一个点与另外一个集合间的所有差值。只需要先询问 \(a \cup S\),然后再询问 \(S\),相同元素删去后就是 \(a\) 与 \(S\) 间的所有差值。
如果我们能够找到区间的最大/小值,那么我们就可以通过上述操作,用差值唯一确定一个数,这使得我们可以直接二进制分组确定所有数。
如何找到最值呢?我们发现,询问任意一个集合,得到的集合中的最大值一定是全局最大值减全局最小值。那么如果某个集合的最大值不等于全局最大值减全局最小值,那么说明这个集合中一定不存在最大值或最小值。那么我们先用 \(1\) 次询问找出全局最大值减全局最小值,就可以在 \(8\) 次操作内二分出这个最大/小值的下标了。我们再通过 \(2\) 次询问,可以确定这个数的值,并且确定这个数是最大还是最小。然后我们就可以通过上述方法进行二进制分组,在 \(16\) 次询问内求出所有数了。总询问次数 \(27\) 次。

继续好似。
被 T1 创死,然后 T2 没推出来,然后成功的似了(
T2 取出排列
简要题意:给定一个排列 \(1, 2, \cdots, n\),进行至多 \(k\) 次操作,每次操作可以将一个数删去,然后放到排列的开头或结尾。\(\forall k \in [0, n)\),求出这样最终能得到的不同的排列数。\(n \le 1000\)。
首先考虑上述操作在干啥:实际上可以理解为从 \([1, n]\) 中任意选取至多 \(k\) 个数,然后将它们任意排列在开头/结尾。而对于一个排列,如果其中的最长上升段的长度大于等于 \(n-k\),那么我们就可以把这段左右的数看作选择的数,那么这个排列是能够得到的。那么实际上,我们只在乎这个排列的上升段的最长段。
最长还是很不好计数,我们考虑先放松一下,求所有连续上升段长度均不超过 \(k\) 的排列数。这个东西是很 GF 的,设一个上升段的 EGF 为 \(F(x)\),那么答案就是 \(\frac{1}{1-F(x)}\)。但是直接这样做有个问题,就是任意放的两个上升段有可能连成一个上升段。
考虑容斥,钦定一些位置必须连起来,其它位置任意。那么对于一个上升段,它就有可能是若干个小上升段连接起来的。这实际上就是一个 OGF 的求逆了。设单个上升段的 OGF 为 \(G(x) = x + x^2 + \cdots + x^k = x\frac{1-x^k}{1-x}\),那么 \(F(x) = \frac{1}{1+G(x)} = \frac{1-x}{1-x+x-x^{k+1}} = \frac{1-x}{1-x^{k + 1}}\)。这个东西的单项系数非常好求,实际上仅在 \((k+1)\) 的倍数或倍数加 \(1\) 的位置有值。那么我们就可以直接利用这个,暴力去计算 \(\frac{1}{1-F(x)}\) 了。根据调和级数,这样做的总复杂度就是 \(O(n^2 \log n)\) 的。
T3 序列 (P7722 [Ynoi2007] tmpq)
Ynoi. Ynoi. Ynoi. Ynoi. Ynoi. Ynoi. Ynoi. Ynoi. Ynoi. Ynoi.
首先 \(b, c\) 数组是没啥意义的,可以直接扔掉。
然后存在一种相对较为好像的操作分块做法。我们可以先把会被修改的所有点与颜色全部标记为关键点。那么接下来我们只需要讨论三个点分别是否为关键点,然后这些情况都可以线性维护出来。然后就是大量分类讨论和写起来很阴间的代码,然后就没了。我懒得再写一遍了。

?
T1 有点过于简单了。不说了。
T2 是个大力容斥题。
T3 有点过于阴间了,咕了。
怎么我考的比较靠前的场就好像都没啥好东西啊((
T2 棋盘
应该是模拟赛考过的题,我有印象见过?
简要题意:给定 \(n \times n\) 的棋盘,有 \(k\) 个格子不能放棋子,并且要求每行每列两个对角线均至少放一个棋子,求放 \(m\) 个棋子的方案数。\(n \le 32, k \le 7\)。
考虑大力容斥,先 \(2^k\) 钦定一些棋子必须放,然后再枚举哪些行列对角线一定不放棋子。
枚举行列有点蠢了,复杂度爆炸。我们可以考虑做一个背包。但是对角线还是比较恶心,我们可以考虑将第 \(i\) 行列与 \(n-i+1\) 行列一起枚举,这样我们就能确定选的这些行列是否与对角线有交点了。然后做个背包容斥下就完了。

不是很差吧。(
T1 实际上用到了一些昨天 T3 的类似做法,我没改但是还是看了的,所以问题不大(
T2 是歌唱王国的强化版,但是我极度弱智导致没有推出来,傻子了属于是。
T3 是个什么阴间建网络流然后分析图的性质然后 手 动 模 拟 D i n i c 的东西。直接弃了,黑盒我可不敢动(
T1 颜色
简要题意:有一棵树,树边有颜色。\(q\) 次询问,每次修改一条边的边权,或询问两个点的路径上是否有颜色相同的两条边。强制在线。\(n \le 10^5\),颜色数 \(\le n\)。
感觉看起来就没有什么很好做的方法。考虑 bitset 直接维护出现颜色集合。我们处理出每个点到根的 bitset,表示这个区间内哪些颜色出现了。为了可以差分,我们使用异或,即记录哪些颜色出现了奇数次。这个并不影响统计,因为 bitset 中 \(1\) 的数量一定是小于等于边数的,我们只需要判断 \(1\) 的个数是不是等于边数即可。那么我们只需要每次将两个 bitset 异或起来,看答案对不对即可。
两个问题:空间开不下,如何修改。
空间开不下的问题,我们可以考虑在树上随机撒一些点,然后只计算这些点到根的 bitset,查询时暴力跳到离它最近的一个关键点。我们撒 \(\omega\) 个点,这样期望下需要跳 \(\frac{n}{\omega}\) 次,这与 bitset 的异或复杂度是一致的,所以这样并不会影响复杂度,空间复杂度降为了线性。
至于修改,容易想到直接根号重构。这个是容易的,不多说了。
T2 字符串

在 nfls 打的最后一场模拟赛。这是不是要掉 rp 了啊(
题目名称也是非常的有趣。
T1 是个超级阴间大分类讨论 DP 题。我调出来了还挺奇迹的,好像基本上 T1 做出来后面随便打打暴力就进前十了,可见 T1 创人之重(
T2 我弱智,并没有意识到 \(\log_{10}(10^{18}) = 18\) 而不是 \(60\)。乐死了。
还没改,口胡一下 T2 吧。
T2 原神怎么你了!(CF924F Minimal Subset Difference)
首先可以发现,我们只关心一个数的数位可重集。可以发现,这样的可重集仅有 \(\dbinom{27}{9} \approx 5 \times 10^6\) 种。这启示我们对可重集进行数位 DP。
首先我们可以预处理出 \(f_{S, len, k}\) 表示当前集合为 \(S\),再放 \(len\) 个数后 \(f(S) = k\) 的方案数。处理出来这个东西之后,询问时只需要直接用预处理出来的答案了。
这样还是不能接受。打表可以发现,大部分 \(S\) 的 \(f(S) = 0/1\),大概仅有 \(2 \times 10^4\) 个 \(S\) 的 \(f(S)\) 不等于 \(0/1\),而且能够到达这些集合的 \(S\) 也只有约 \(3\times 10^4\) 个。这样我们仅对这些数处理上述 DP,复杂度减小了很多。
那么我们如何计算 \(f(S) = 0/1\) 的 \(S\) 呢?很简单,我们不计算。
考虑容斥得出。对于 \(k \ge 1\) 的询问,我们只需要拿总数减去 \(> k\) 的即可。对于 \(k=0\) 的,我们有一个重要的发现,就是 \(f(S)\) 的奇偶性一定与 \(S\) 的和的奇偶性一致。而求 \(S\) 的和为偶数的方案数是很容易的,于是我们可以拿总和为偶数的方案数减去 \(k \ge 2\) 的偶数的答案,就是 \(0\) 的答案了。
询问的时候可能复杂度还是有点高,我们可以再预处理出一个前缀和的东西,这样询问时就不用枚举开头选什么了。