526互联

Solution Set - “让朝阳洒向晚霞，在星空下涂鸦”

发布时间 2023-06-16 15:11:33作者: Rainybunny

目录

\[\mathbf{Defining~\LaTeX~macros\dots} \newcommand{\opn}[1]{\operatorname{#1}} \newcommand{\lcm}[0]{\opn{lcm}} \newcommand{\anc}[0]{\opn{anc}} \newcommand{\lcp}[0]{\opn{lcp}} \]

  有相当一部分是在清 to-do list, 所以星星比较多.

0.「UR #12」「UOJ #182」a^-1 + b problem

  显然在任意时刻 \(t\), 总存在 \(A_t,B_t,C_t,D_t\), 使得 \(a_{i,t}=\frac{A_ta_i+B_t}{C_ta_i+D_t}\). 当 \(C_t=0\), 求和是容易的, 我们只需要考虑 \(C_t\neq0\) 的情况. 此时 \(a_{i,t}\) 可以写作 \(p_t+\frac{q_t}{a_i+r_t}\), 快速求出 \(\sum_i\frac{1}{a_i+r_t}\) 是剩下的任务.

\[\begin{aligned} \textit{res}_t &= \sum_{i=1}^n\frac{1}{a_i+r_t}\\ &= \frac{\sum_{i=1}^n\prod_{j\neq i}(a_j+r_t)}{\prod_{i=1}^n(a_i+r_t)}\\ &= \left.\frac{A'(z)}{A(z)}\right|_{z=r_t} \end{aligned} \]

其中 \(A(z)=\prod_{i=1}^n(a_i+z)\). 跑一堆分治 FFT 和多点求值就行, \(\mathcal O(n\log^2n)\).

1.「NOI Simu.」点 ⭐

  补不动今天的题就补补上周的题吧 (悲).

  挺厉害的东西. 先令 \(x_i\gets x_i+d\), 再令 \(d\gets2d\), 这样每个点要不不动, 要不向前跳 \(d\) 步. 设坐标范围为 \(m\), 我们有一个简单的 \(\mathcal O(m2^d)\) 的大暴力. Key 的地方在于 \(150\) 这玩意儿的确不能跑非 poly, 但 \(\sqrt{150}\) 之类的范围就可以随便指数级了. 也就是说, 我们只需要再整一个关于 \(m/d\) 的指数级算法就能平衡出正解.

  提示很明显, 将坐标每 \(d\) 个排成一行, 得到一个方阵. 现在每个点要不不动, 要不在方阵上向上方跳一格. 记录列的状态大力 DP 就行. 不过我们需要钦定第一列的状态, 因为最后一列和下一行第一列会拼起来算贡献. 这样就有一个 \(\mathcal O(m2^{2m/d})\) 的算法. 平衡一下, 就得到了 \(\mathcal O(m2^{\sqrt{2m}})\) 的算法, 可以通过.

2.「集训队互测 2023」「QOJ #5100」卡牌游戏 ⭐

  复杂度平衡是不是大势所趋呀…

  大力 DP 有 \(f(i)=\max_{j<i}\{f(j)+S-S\bmod\lcm(a_i,a_j)\}\), 注意到 \(S\bmod ka\ge S\bmod a\), 而我们在求 \(\max\), 所以 \(\lcm\) 的约束可以放宽为:

\[f(i)=\max_{d\mid a_i}\{\max_{j<i\land d\mid a_j}\{f(j)-S\bmod(a_ia_j/d)\}\}+S. \]

  对于一组转移 \(j\to i\), 若 \(\min\{a_i,a_j\}<\sqrt S\), 有效转移只有 \(\mathcal O(n\sqrt S)\) 个 (显然末尾数值相同时, 序列越长越好). 当然这个界可以缩紧: 注意到一对 \((a_i,a_j)\) 对答案的贡献要不为 \(0\), 要不 \(\ge S/2\). 又因为两个 \(<\sqrt S\) 的数相邻选择, 对答案的贡献一定非 \(0\), 所以 \(j\to i\) 之间不能有超过 \(3\) 个 \(<\sqrt S\) 的数 (不然无脑选上所有这样的数更优).

  于是, \(<\sqrt S\) 的转移是线性的. 利用上述结论, 带上最优性剪枝暴力做上面的转移, 大概就是 \(\mathcal O(n\sqrt S)\) 的? 然后再来看看第二问, 前缀和后缀状态拼接, 中间区间仍然有上述结论, 我们可以得到 \(\mathcal O(n\sqrt S)\) 个区间取 \(\max\) 操作, 挂到喵喵树上处理就行, 还是 \(\mathcal O(n\sqrt S)\).

  你要问兔的代码怎么写的暴力更新: zak 能用暴力过兔就不能吗? (大雾

3.「NOI Simu.」简单的签到题

  无修的情况, Hall 定理判一判就行. 我们从高到低枚举 Hall 定理的判据 \(\sum_i[b_i\ge k]\le\sum_u[\forall v\in\anc(u),~a_v\ge k]\) 中的 \(k\), 在右式产生贡献的 \(u\) 将同 BFS 一样逐步扩展. 当第一个不合法的 \(k\) 出现时, 队列里剩下的点就一定成为我们的修改目标.

  比较无脑的做法是, 枚举修改目标, 二分其修改到的值, 再枚举其子树重新计算 Hall 定理的贡献. 用线段树维护贡献检查 Hall 定理, 可以做到 \(\mathcal O(n\log^2n)\). 可以过, 但你的常数需要不劣于兔子卡常后的常数.

  "二分其修改到的值" 这一步其实是不必要的. 我们找到第一个不满足 Hall 定理判据的 \(k\), 直接将修改目标的值设为 \(k\). 此时, 若子树内的某个结点已经在 \(k\) 处贡献, 则 \(k\) 变大也产生不了更多贡献; 若某个结点仍然未在 \(k\) 处贡献, 证明其还受到其他瓶颈限制, 增加 \(k\) 也无奈何它. 因而有且仅有这个 \(k\) 是有意义的检查. 这样复杂度就是 \(\mathcal O(n\log n)\) 了.

4.「NOI Simu.」简单的字符串题 ⭐

  答案分母容易用 SA 或者 SAM 算出来. 对于无序对 \((i,j)\), 设其的贡献为所有以 \((i,j)\) 为各自左端点的字符串对的贡献总和. 当 \(i=j\), 答案也容易计算. 不妨设 \(i<j\), 此时 \((i,j)\) 的贡献显然是 \(\max\{0,\lcp(S[i:],S[j:])(\lcp(S[i:],S[j:])+1)\}\). 重点便是统计这类贡献.

  这里有个 trick, 我们可以按照 \(d=j-i\) 将无序对分类求答案, 其本质是利用了 \(i,j\) 同步移动时, LCP 信息具有继承关系这一性质.

  枚举 \(d\), 所有的区间 \([i,j]\) 都必然会包含某个 \(kd\), 而又因为所有有贡献的 \((i,j)\) 的 LCP 至少为 \(d\), 所以此时它们的 LCP 部分一定对应了一个跨过 \(kd\) 的字符串和一个与之相同的跨过 \((k+1)d\) 的字符串. 我们枚举 \(kd\), 分别求出 \(kd\) 和 \((k+1)d\) 向前和向后各自能匹配的字符串长度, 则所有被匹配的到位置对应的 \((i,j)\) 的 LCP 从左到右递减, 我们可以一下子求出它们的贡献和, 当然这里需要记录上一次匹配到的右端点用于去重. 最终复杂度 \(\mathcal O(n\log n)\).

5.「NOI Simu.」简单的 bzoj 题 ⭐

  费用流做法是存在的 (模拟费用流 ver: link), 所以区间答案关于树的数量是凸的, 暴力 Minkowski 和在线段树上合出所有凸包, 区间询问时先 WQS (本质上是在二分询问区间对应的凸包上的点), 然后依次扫描线段树结点上的凸包, 再拿着 WQS 的斜率二分最佳转移位置, 这样可以得到一个丑陋但能过的 \(\mathcal O((n+q\log^2n)\log n)\).

  考虑优化掉 "二分最佳转移位置": 将所有询问的拉在一起 "整体 WQS 二分", 这样每个线段树区间就可以维护一个指针单调确定转移位置, 少一个 \(\log\).

6.「UR #18」「UOJ #484」绝对不鸽 ⭐

  好抽象啊你这题, 还有你这题的各种题解! ?

  特判 \(n=B\) 的情况, 不表. 这题麻烦的地方在于对一个位置的重复增加和推平, 这让我们很难去描述序列状态, 也就很难看出有效的贪心策略.

  因而, 第一步的转化, 我们把序列展开到无限长. 初始时 \(\{a_n\}\) 在序列左端不降排列, 序列其余位置全部为 \(0\). 每次操作时, 任意选若干个位置总共\({}+A\), 并要求序列保持不降, 然后删除序列前 \(B\) 个位置. 操作目标仍然是最大化某个时刻的最大值.

  不难发现, 最大值一定在 \(k=xB+1\) 处取到. 如果 \(k\) 被固定, 操作策略显而易见: \(k\) 的前缀中第一个可以增加的位置\({}+1\), 重复 \(A\) 次. 当 \(k>n+B\), 初始的 \(\{a_n\}\) 已经不影响答案, 结果就是 \(\{a_n\}\) 全部取 \(0\) 的结果. 当 \(k\in(n,n+B]\), 我们可以暴力模拟一轮操作, 现在就只需要考虑 \(k\in[1,n]\) 的情况. 设 \(f(i)\) 表示剩下 \(iB+1\) 个数, 答案在 \(iB+1\) 位且这些数分布均匀 (极差 \(\le 1\)) 时, 它们的和的最大值. 当 \(k\) 固定, 在若干轮后一定存在某个 \(p\), 使得 \([p,k]\) 内的数是均匀的. 用这个区间更新 \(f\). 此外考虑 \(k>n+B\) 的情况, 相当于恒定有 \(n-B\) 个 \(\lfloor(A-1)/B\rfloor\) 和 \(B\) 个 \(0\), 这也可以拿来更新 \(f\).

  最后, \(f\) 代表的稳定状态之间也能产生转移, 即在 \(iB+1\) 这个序列的基础上再操作一次转移向 \((i-1)B+1\). 最终的 \(f(0)\) 就是答案. 双指针维护 \(p\) 可以做到 \(\mathcal O(n\log n)\), 瓶颈是排序.

7.「LOJ #6734」图上的游戏 ✡️

  • Link & Submission.
  • 「A.构造」「A.分治-二分答案」「C.思维」
Stop learning useless algorithms,
go and solve some problems,
learn how to use binary search!

  哎, 好难调啊.

  结合部分分, 我们可以大概猜出三个问题阶段: 找生成树边, 建生成树, 找非树边.

  找树边, 我们可以对每个点二分删除多长的边集后缀后它与 \(0\) 不连通, 那么最后一条边一定可以加入树边集合. 如此迭代直到不存在这样的后缀, 此时这个点和 \(0\) 就被已知树边连接起来了. 这部分询问次数是 \(\mathcal O(n\log m)\).

  建生成树, 是个麻烦的部分. 我们先二分找到每个点 \(u\) 树上祖先边中编号最小的一条, 记编号为 \(s_u\). 此时取出 \(S=\arg\min\{s_u\}\), 则 \(S\) 一定构成一棵完整的子树. 我们先递归处理 \(U\setminus S\), 然后对 \(S\) 内的点 \(u\) 再次二分出 \(s_u'\) 表示子树内祖先边中编号最小的一条. 一定存在一个点 \(r\in S\), 它的 \(s_r'\) 不存在, 因为它就是 \(S\) 的子树根, 这样我们就得知了 \(r\) 的父边是刚才的的 \(\min\{s_u\}\). 最后递归 \(S\setminus\{r\}\), 我们就求出了所有父边信息. 随机化树边编号, 每个点期望需要求 \(\log\) 次 \(s_u'\), 每次求解暴力二分, 这部分询问次数是 \(\mathcal O(n\log^2n)\).

  但是… 得到父边信息也没办法直接建树, 我们还需要知道每个点的父亲究竟是谁. 设序列 \(V\) 为上述递归过程中依次取出的 \(r\) 构成的序列, 可以发现这个序列是一种可能的 BFS 序 — 对于 \(u\) 的深度 \(<\) \(v\) 的深度, 则 \(u\) 出现在 \(v\) 的左侧. 这有什么作用呢? 一个点 \(u\) 的父亲 \(x\), 可以描述为 "断掉 \(x\) 的父边, 使得 \(u\) 不与 \(0\) 连通" 的深度最深的 \(x\) (若 \(x\) 不存在, 父亲为 \(0\)), 我们在 \(V\) 上二分这个 \(x\) 即可. 这里的询问次数是 \(\mathcal O(n\log n)\).

  最后是求非树边, 这也挺轻松. 枚举 \(u\), 尝试找到以 \(u\) 为其中一个端点的非树边, 将 \(u\) 到父亲的树边删除, 二分得到第一个让 \(u\) 仍然能连向 \(0\) 的边集后缀, 此时我们找到了一个非树边编号, 再在树上二分删掉另一条父边, 找到这条非树边的另一个端点即可. 这里的询问次数是 \(\mathcal O(n\log n)\).

  妈妈生的, 原来 \(\mathcal O(n\log^2n)\) 过不去啊! (这部分是上个月写的, 弃疗了.)

  歪歪! 这里是一个月之后的兔子, 她学了建生成树的正解, 把题解补上啦!

  把建生成树再划分成两个子步骤: 首先得到树的任意一种链剖分方案. 每条链保存链中结点集合, 链中边集合, 以及链的父亲是哪条链. 接着从浅到深处理每条链: 先在链的父亲的链 (已经被处理) 中二分到链顶父亲, 然后对链处理完全确定信息 (包括父边编号, 父亲编号等等).

  链剖分, 每次取出一个结点 \(u\), 二分找到所有未被剖分的边中, \(u\) 的祖先边集 \(S\). 若 \(S\) 为空, \(u\) 必然属于某条已经存在的链, 再在链集合里二分具体归属. 若 \(S\) 非空, 则新建一条链, \(\{u\}\) 作为点集 (此后还会加入其他点), \(S\) 作为边集 (保持不变), 在同上二分求得这条链的父亲链. 完成第一步.

  对链处理, 我们需要处理形如 "已知链顶 \(x\), 链中非顶的点集 \(S_V\), 链中边集 \(S_E\), 求出链的信息". 每次随机在 \(S_V\) 中取出一个点 \(u\), 暴力询问将 \(S_V,S_E\) 划分为在 \(u\) 之上的集合和在 \(u\) 之下的集合, 分治求解. 期望复杂度单 \(\log\), 这样就完成建树了.

  最终询问次数是 \(\mathcal O(n\log n)\), 步骤多常数大, 兔写出来的东西需要很多奇怪的卡常.

8.「集训队作业 2021」「洛谷 P7353」Tom & Jerry ⭐

  • Link & Submission.
  • 「A.图论-缩点/圆方树」「C.性质/结论」

  直接放到圆方树上考虑. 以 Tom 的起点 \(a\) 为根, 如果 Tom 希望把 Jerry 逼入某棵子树 \(u\) 内, 就必须保证: 从 \(a\) 到 \(u\) 的圆方树路径中, 相邻圆点在原图上仍相邻. 我们称这样的 \((u,a)\) 是好的.
  先编几个 Tom 胜利的充分条件. 我们发现, 若删掉 \(a\) 后 \(b\) 所在连通块中所有点 \(u\) 都满足 \((a,u)\) 是好的, 那么 Tom 显然可以将 Jerry 逼入死路. 此外, 若存在某个点 \(x\), 使得 \(x\) 到其他任何点都是好的, Tom 也可以先悠哉地走到 \(x\) 在逼迫 Jerry.

  不出题解所料, 这两个条件或在一起就必要了. 在不满足这两个条件的情况下, 当 Tom 走到一个点 \(x\) 时, 尝试找到一个使 \((x,y)\) 不好的 \(y\), 使得 Jerry 能够跑到 \(y\). 若不然, 即 \(x\) 在 Jerry 到 \(y\) 的必经之路上, 那么由于 \((a,y)\) 也一定不好, Jerry 可以在此之前就到达 \(y\).

  接下来就是求答案的过程. 令 \(f(u)\) 表示圆点 \(u\) 或方点 \(u\) 的父亲是否到子树内的任意一点都是好的, 转移显然. 令 \(g(u)\) 表示圆点 \(u\) 或方点 \(u\) 的父亲到 \(u\) 子树外的任意一点都是好的, 对于圆点 \(u\), \(g(u)\) 为真的条件为:

  • \(g(p_{p_u})\) 为真.
  • \(u\) 所在点双内的任意一点均与 \(u\) 直接相连 (可通过子图内度数判断).
  • 所有 \(u\) 的兄弟的 \(f\) 为真.

  若不存在 \(f(u)=g(u)=\textbf T\) 情况, 我们需要判定第一种获胜判据. 若 \(a\) 不是 \(b\) 的祖先, 我们就要求 \(g(a)=\textbf T\), 否则就要求 \(b\) 最接近 \(a\) 的祖先 \(c\) 的 \(f(c)=\textbf T\). \(\mathcal O(n\log n)\) 不难实现.

9.「BJOI 2016」「洛谷 P6839」打字机

  有一种打火机题特有的美感. (

  Subtask A \((m\le500)\) 设 \(f(u,\ell,c)\) 表示从 AC 自动机上结点 \(u\) 出发打长度为 \(\ell\) 的串, 最多失误 \(c\) 次的答案. 不失误的 \(\max\) 转移和失误的 \(\min\) 转移再取个 \(\min\) 就是转移. 设 \(L=\sum_i|S_i|\), 复杂度 \(\mathcal O(Lmk|\Sigma|)\).

  Subtask B \((k=0)\) 典. 矩阵快速幂. \(\mathcal O(L^3\log m)\).

  Subtask C \((L\le50,~a_i=1)\) 这个 \(a_i=1\) 是什么玩意儿? 感觉这个问题应该仍然不弱于矩阵快速幂. 好吧, \(L\) 很小 \(a_i\) 也很小, 捉弄打字员的我们也没有必要把失误隔得很远来 "下一盘大棋". 可以猜测失误集中在最后 \(m'=2\times10^3\) 步以内也能得到正确答案, 融合 Subtask A 和 B 的做法算一算就行. 复杂度 \(\mathcal O(Lm'k|\Sigma|+L^3\log m)\).

10.「UR #14」「UOJ #194」思考熊 ⭐

  • Link & Submission.

  • 「A.树论-点分治/点分树」「C.细节」(其实是边分树, 但懒得加 tag 了.

  嘶哈嘶哈卡常题. 题解是什么二进制分组+虚树? 不如在 \(3\times10^5\) 个结点的树上对 \(6\times10^5\) 的三度化树进行边分治得到 \(1.2\times10^6\) 的边分树再于其上维护倍增长度线段树跑 \(\log^2\) 算法轻松过题. (雾

  嗯, 思路就是这样, 这里忍痛采用巨大常数的边分树是为了减少线段树结点的信息量卡空间. 线段树需要像 std::vector 的内存分配策略一样处理: 先开长度为 \(1\) 的线段树, 当长度为 \(\ell\) 的线段树被插满结点后将其扩大到 \(2\ell\) 暴力重构. 因为线段树长度一直是 \(2\) 的整幂, 所以很多线段树操作可以非递归进行 (当然也推荐 zkw 线段树, 只是兔不会). 总之这题就 \(\mathcal O(q\log^2n)\) 的时间, \((2+1)\times4\times2q\log_{1.5}(2n)+\mathcal O(n)~(\text{bytes})\) 的空间卡过了.

11.「UNR #1」「UOJ #214」合唱队形

  • Link & Submission.
  • 「A.DP-状压/插头 DP」「B.复杂度平衡」

  \(n=30\)? 鉴定为两个指数级平衡. 当 \(n-m\) 比较小的时候, 匹配模式串的可行位置较少, 直接丢一个 Min-Max 反演就行. 当 \(m\) 比较小的时候, 有效字符集大小, 模式串长度较少, 考虑用 未完成状态 * 出现概率 * 产生第一次有效状态变化的期望步数 统计答案, 一个稍微麻烦一点的 DP. 最终可以平衡到 \(\mathcal O(2^{n/2}\text{poly}(n))\). (但是, 兔的代码里有依托 \(2^{2m}\) 的答辩 DP.)

12.「UNR #1」「UOJ #217」奇怪的线段树 ⭐

  你是一种很新的道路铺设.

  考虑按子树贪心. 在子树根处将发生如下事件:

  1. 左子树内靠着右端的覆盖区间与右子树内靠着左端的覆盖区间合并.

  2. 左子树是黑色树的叶子:

    1. 若右子树有靠着左端的覆盖区间, 直接将它延长覆盖左侧.

    2. 或者, 若右子树中有过 (1) 情况中的合并, 且对应的区间可以进行 (2.1) 中的覆盖, 则将这个合并拆开, 然后进行 (2.1).

    3. 否则, 不得不新增一个 (对于当前子树根) 靠着左端点的覆盖区间, 覆盖之.

  3. 右子树是黑色树的叶子, 同理.

  可以感知到局部最优性和全局最优性, 那么写上去就跑路了. (具体实现可以看代码, 短且有一定注释.)

  不想推贪心咋做啊? 当然, 如同道路铺设, 这里也存在线规对偶然后 DP 的做法, 具体可以问问 crashed. 两种算法都是 \(\mathcal O(n)\) 的.

13.「LOJ #6681」yww 与树上的回文串 ⭐

  • Link & Submission.

  • 「A.树论-点分治/点分树」「A.字符串-ACAM」「A.字符串-回文相关」

  我们势必会通过某种方式处理回文串的合并问题, 但可以发现这其实挺棘手的: 不知道回文中心, 拆成两半的串很难判定能否合成回文, 而 hash 之类的办法又没办法支持批量合并. 这怎么办呢?

  想想我们的 border 论: 一个字符串的 border 序列可以被划分入 \(\log\) 个等差序列. 考虑点分治结构中:

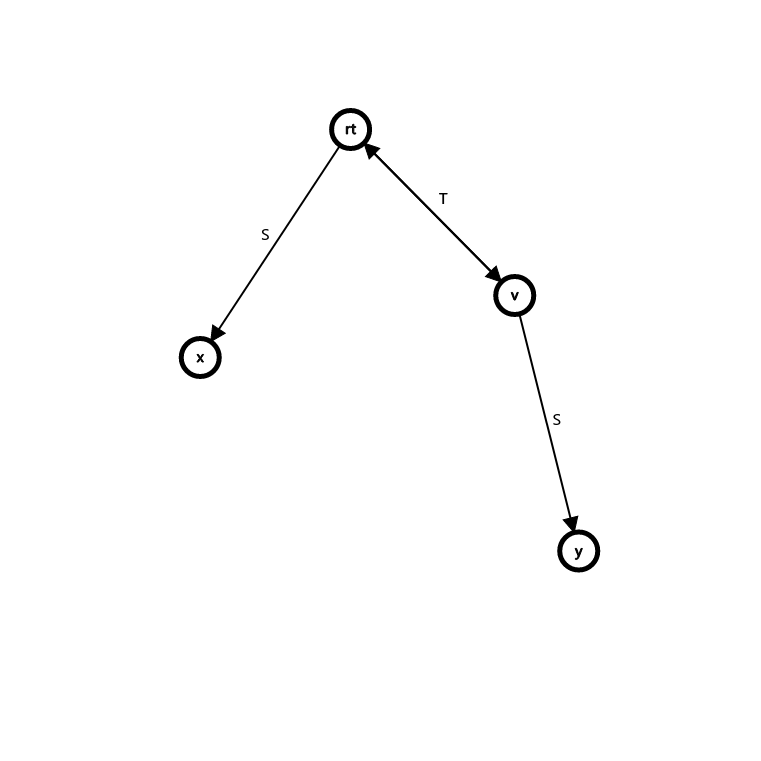
graph.png

对于分治中心 \(r\) 到某点 \(y\) 的路径 \(r\to y\), 如果它和 \(r\to x\) 形成了形如上如的回文, 那么 \(T\) 一定是 \(r\to y\) 的串的一段回文前缀. 任意回文前缀是最长回文前缀的 border, 因此回文前缀也可以用 border 等差序列的结论!

  顺着这个思路, 我们尝试计数, 这里仅讨论复杂一些的 \(T\neq\varnothing\) 的情况. 在 AC 自动机的 fail 树上, \(r\to x\) 对应的 \(S\) 是 \(T+S\) 的祖先. 暴力方法很简单: DFS fail 树, 到达 \(y\) 对应的串结点时, 将 \(T+S\) 中所有可能 \(T\) 枚举出来, 将对应的 \(S\) 的长度作为询问, 然后在祖先的对应位置贡献答案并删掉这些询问. 子树结构保证了长度信息可以唯一确定 \(S\), 这样就得到了一个方便的做法.

  添加上 border 的优化, 我们需要在出现次数关于长度的桶上快速等间距求和, 直接根号分治, 小范围预处理, 大范围暴力跳就行. 主定理出来 \(\mathcal O(n\sqrt n)\), 除此之外的 \(\text{polylog}\) 部分就可以写得很随意了.

14.「UR #14」「UOJ #192」最强跳蚤

  "所有素因子出现偶数次", 经典异或 hash, 瓶颈在于素因子分解, 比较好写的有 \(\mathcal O(n\sqrt V/\ln V)\) 的枚举根号以内素数的做法. 统计答案的时候, 有个睿智兔子写的点分治, 这明显是前面几道题给整上头了. (

15.「NOI Simu.」隔膜

  一眼丁真, 鉴定为 So Many Possibilities...