1 试给出下述博弈的纳什均衡

解:由划线解得知有一个纯纳什均衡(D,R )。再看看它是否有纳什均衡,设B的混合策略为\((\gamma,1-\gamma)\),则有
均衡条件:
得 \(\gamma=4>1\), 这是不可能的, 故无混合纳什均衡, 只有这一个纯纳什均衡。
2 修改题1中的收益值使其有混合纳什均衡
解:由奇数定理,若使它先有两个纯纳什均衡,则很可能就有另一个混合纳什均衡。

将博弈改成上述模型, 则
同样, 设 \(A\) 的混合策略为 \((\theta, 1-\theta)\), 则
于是混合纳什均衡为 \(\left\{\left(\frac{1}{2}, \frac{1}{2}\right),\left(\frac{4}{5}, \frac{1}{5}\right)\right\}\) 。
3 Mixed strategy equilibrium of Hawk-Dove
Denote by \(u_i\) a payoff function whose expected value represents player i's preferences. The conditions in the problem imply that for player 1 we have
and
Given \(u_1\) (Aggressive, Aggressive \()=0\) and \(u_1\) (Passive, Aggressive \(=1\), we have
and
so that
Similarly,
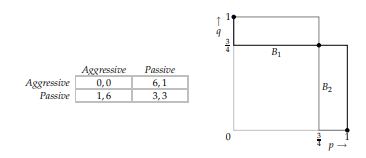
Thus the game is given in the left panel of Figure 25.1. The players' best response functions are shown in the right panel. The game has three mixed strategy Nash equilibria: \(((0,1),(1,0)),\left(\left(\frac{3}{4}, \frac{1}{4}\right),\left(\frac{3}{4}, \frac{1}{4}\right)\right)\), and \(((1,0),(0,1))\).
4 Checking for subgame perfect equilibria
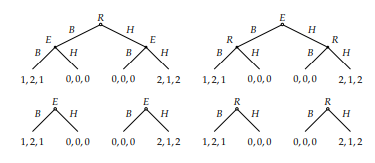
The Nash equilibria \((C H, F)\) and \((D H, E)\) are not subgame perfect equilibria: in the subgame following the history \((C, E)\), player 1's strategies \(C H\) and \(D H\) induce the strategy \(H\), which is not optimal.
The Nash equilibrium ( \(D G, E)\) is a subgame perfect equilibrium: (a) it is a Nash equilibrium, so player 1's strategy is optimal at the start of the game, given player 2's strategy, (b) in the subgame following the history \(C\), player 2's strategy \(E\) induces the strategy \(E\), which is optimal given player 1's strategy, and \((c)\) in the subgame following the history \((C, E)\), player 1's strategy DG induces the strategy G, which is optimal.
5 用逆向归纳法求解不完全信息动态博弈的子博弈完美纳什均衡

解:设在 1 的第二个信息集上, 1 认为 2 选 \(a\) 的概率为 \(P\),则 1 选 \(L^{\prime}\) 的支付 $$=5 P+2(1-P)=2+3 P$$;1 选 \(R^{\prime}\) 的支付 $$=6P+3(1-P)=3+3 P>2+3P$$,故1必选 \(R^{\prime}\) 。
即得\(\Rightarrow\) 给定 1 在第二个决策结上选 \(R^{\prime}, 2\) 在左边决策结上会选 \(a\), 故子博弈完美纳什均衡为\(\left\{L, R^{\prime},(a, d)\right\}\)。
6 Cournot's duopoly game with imperfect information
The best response \(b_0\left(q_L, q_H\right)\) of type 0 of firm 1 is the solution of
The best response \(b_{\ell}\left(q_L,q_H\right)\) of type \(\ell\) of firm 1 is the solution of
and the best responese \(\mathrm{d}(\mathrm{fu}, \mathrm{fu})\) ef bype hit of firme 1 is the solutice of When \(P(Q)=a-Q\) foe \(Q \leq a\) and \(P(Q)=0\) for \(Q>a\) we tind, after weme reviring algera, that
When \(\pi=0\) we hure enerciue
Whes \(\pi=1\) we have
wo thes \(q_1\) and of are the same as the equilbrium outputs when thene is perfect ane \(c\) and \(6 \mathrm{~s}\).
Now, for an arbitrary value of \(\pi\) we have
To show that foe \(0<a<1\) the values of these variatles lis between their value when \(z=0\) and when \(z=1\), we novd so show that
and
3 巴什博弈
巴什博弈属于基本的博弈问题,其典型特征为:给定\(n\)堆物品,两个人轮流从这堆物品中取物品,规定每次最少取1个,最多取\(m\)个,最后取光者为胜。
当\(n=m+1\)时,由于一次最多只能取\(m\)个,所以无论先取者拿走多少个,后取者都能一次拿走剩余的物品,后取者取胜;当\(n=(m+1)×r+s\)(其中\(r\)为任意自然数,\(s \leq m\)),如果先取者要取走\(s\)个物品,如果后取者取走\(x(x \leq m)\)个,那么后取者只要取走\(m+1−x\)个,结果剩下\((m−1)(r−1)\)个,以后保持这样的取法,那么先取者肯定获胜,总之,要保持给对手留下 \((m+1)\)的倍数,就能最后获胜。
结论1:若\((m+1)∣n\),则先手必败,否则先手必赢。
结论2:当\((n−1)\%(m+1)=0\)时先手必输。
4 威佐夫博弈
有两堆各若干个物品,两个人轮流从某一堆或同时从两堆中取同样多的物品,规定每次至少取一个,多者不限,最后取光者得胜。
如何解决威佐夫博弈问题?
首先,我们定义\((a_i, b_i) (a_i \leq b_i, i = 1, 2, ..., n)\)表示两堆物品的数量并称其为局势,如果甲面对\((0,0)\),那么甲已经输了,这种局势我们称为奇异局势。前几个奇异局势,前几个奇异局势为\((0,0)、(1,2)、(3,5)、(4,7)、(6,10)、(8,13)、(9,15)、(11,18)、(12,20)\)。任意给定一个局势\((a,b)\),如下公式可以判断其是否为奇异局势:
\(a_k = \lfloor \frac {k \times (1 + \sqrt{5})}{2} \rfloor, b_k = a_k + k \quad (k = 0, 1, 2, ..., n)\)
面对非奇异局势,先手必胜;面对奇异局势,先手必败。
5 斐波那契(Fibonacci)博弈
斐波那契博弈的典型特征是:给定一堆个数为\(n\)的石子,两个玩家轮流取石子,满足:先手不能在第一次把所有的石子取光;第一次取完后的每次可以取得石子数介于1到对手刚取的石子数的2倍之间(包含1和对手刚取的石子数的2倍);取走最后一个石子的人为玩家。
如何解决这一类博弈问题?
首先先给出结论:当\(n\)为斐波那契数的时候,先手必败,即存在先手的必败态当且仅当石头个数为Fibonacci数。
下面给出证明:
根据“Zeckendorf定理”(齐肯多夫定理):任何正整数可以表示为若干个不连续的Fibonacci数之和。如\(n=83=55+21+5+2\),我们看看这个分解有什么指导意义:假如先手取2颗,那么后手无法取5颗或更多,而5是一个Fibonacci数,那么一定是先手取走这5颗石子中的最后一颗,同理,接下去先手取走接下来的后21颗中的最后一颗,再取走后55颗中的最后一颗,那么先手赢。
反证:如果\(n\)是Fibonacci数,如\(n=89\):记先手一开始所取的石子数为\(y\)
(1)若\(y \geq 34\)颗(也就是89的向前两项),那么一定后手赢,因为89−34=55=34+21<2∗34。
(2)若\(y<34\)时剩下的石子数\(x\)介于55到89之间,它一定不是一个Fibonacci数,把\(x\)分解成Fibonacci数:\(x=55+f[i]+…+f[j]\),若,如果\(f[j]<=2y\),那么对B就是面临\(x\)局面的先手,所以根据之前的分析,后手只要先取\(f[j]\)个即可,以后再按之前的分析就可保证必胜。
判断斐波那契数的方法可以采用通项公式法或遍历法。如果数据范围大会卡时间则考虑矩阵快速幂优化等。
6 Nim博弈
Nim游戏是一个典型的博弈问题,建立在Nim游戏基础上的博弈一般都具有相同的框架特征。
\(n\)堆物品,每堆有\(a_i\)个,两个玩家轮流取走任意一堆的任意个物品,但不能不取。取走最后一个物品的人获胜。
例如,如果现在有\(n=3\)堆物品,而每堆分别有2,5,4 个,那么可以取走第1堆中的2个物品,局面就变成了0,5,4;或者也可以取走第2堆的4个物品,局面就变成了2,1,4。如果现在的局面为0,0,5,甲取走了第3堆的5个物品,也就是取走了最后一个物品,此时甲获胜。
首先回顾“博弈图”。我们通过绘画博弈图,可以在 \(O\left(\prod_{i=1}^n a_i\right)\) 的时间里求出该局面是否先手必赢。
显然,这样的推导方式时间复杂度是非常高的,我们需要换一种思路进行推导。
定义 \(\operatorname{Nim}\) 和 \(=a_1 \oplus a_2 \oplus \ldots \oplus a_n\)。那么当且仅当 Nim 和为 0 时,该状态为必败状态;否则该状态为必胜状态。
如何证明Nim和的正确性? 为什么异或值会和和状态的胜负有关?
为了证明该定理,只需要证明下面三个定理:
定理 1: 没有后继状态的状态是必败状态。
定理 2: 对于 \(\mathrm{a}_1 \oplus \mathrm{a}_2 \oplus \ldots \oplus \mathrm{a}_{\mathrm{n}} \neq 0\) 的局面,一定存在某种移动使得 \(\mathrm{a}_1 \oplus \mathrm{a}_2 \oplus \ldots \oplus \mathrm{a}_{\mathrm{n}}=0\) 。
定理 3 : 对于 \(\mathrm{a}_1 \oplus \mathrm{a}_2 \oplus \ldots \oplus \mathrm{a}_{\mathrm{n}}=0\) 的局面,一定不存在某种移动使得 \(\mathrm{a}_1 \oplus \mathrm{a}_2 \oplus \ldots \oplus \mathrm{a}_{\mathrm{n}}=0\)
对于 定理 1 ,没有后继状态的状态只有一个,即全 0 局面。此时 \(\mathrm{a}_1 \oplus \mathrm{a}_2 \oplus \ldots \oplus \mathrm{a}_{\mathrm{n}}=0\) 。
对于 定理 2 ,不妨假设 \(a_1 \oplus a_2 \oplus \ldots a_n=k \neq 0\) 。如果我们要将 \(a_i\) 改为 \(a_i^{\prime}\) ,则 \(a_i^{\prime}=a_i \oplus k\) 。 \(\mathrm{k}\) ,因而这也是个合法的移动。
对于 定理 3 ,如果我们要将 \(a_i\) 改为 \(a_i^{\prime}\) ,则根据异或运算律可以得出 \(a_i=a_i^{\prime}\) ,因而这不是个合法的移动。