这个东东呢我之前好像写过,但是由于我之前写的特别丑导致我看不懂了 QAQ
所以我来写一篇有图片的,清晰易懂的详解。
manacher 可以用来求出一个字符串的最长回文子串。
首先回文子串有两种——长度为奇数的和长度为偶数的,比如 aba 长度是奇数,中心为 b,但是 abba 长度为偶数,中心就是那个缝隙。为了方便我们处理,我们可以这样来,在每两个字符之间插入一个不会出现的符号,比如 #,在字符串最开头也要加一个防止越界。所以,比如一个字符串 aba 就会变成 ##a#b#a#。其实这个井号还有别的一个很巧妙的用处,我们在下面讲。
下面我们定义 \(f_i\) 为以 \(i\) 为回文中心的最长可以往左右延伸的长度,也就是回文半径(加了井号过的,下面的字符串一律按照加了井号过的处理),那么比如 ababba 的话, f 就是酱紫的
# # a # b # a # b # b # a #
f 0 0 1 0 3 0 3 0 1 4 1 0 1 0
我们仔细观察,发现了什么没有?在加了井号的字符串里面 的 \(f_i\) 就对应着 不加井号的 原串 的以 \(i\) 为回文中心的 回文串长度!这是因为我们每个都加了一个井号。
说了这么多,那么核心就是要求这个 \(f\),怎么求呢?一个一个找太慢了,我们要充分利用已知信息。
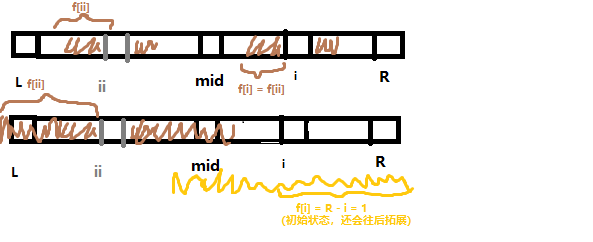
我们令已经处理好了 \(f_{1} \sim f_{i - 1}\),当前处理到了 \(i\) 也就是要求 \(f_i\) 了,之前向右最远拓展到了 \(R\),回文中心是 \(mid\),我们令 \(L = 2mid - R\)(就是它左端点),\(ii = 2mid - i\)(\(i\) 关于 \(mid\) 的对称点)。
当 \(i \le R\) 时 我们知道左边和右边是对称的。既然知道了 \(f_{ii}\),把 \(ii\) 的回文串对称过来,它肯定还是回文串,还是 \(i\) 的回文串,所以我们就可以令 \(f_i = f_{ii}\)。注意,如果 \(f_{ii}\) 其实伸过了 \(mid\) 的话,那么有一段我们是不能把它对称过去的,这时候 \(f_i = R - i + 1\),当然后面还要继续拓展。
当 \(i > R\) 时,\(f_{i}\) 无法得知有效信息,只能从 \(0\) 开始。
代码
//SIXIANG
#include <iostream>
#include <string>
#define MAXN 3 * 10000000
#define QWQ cout << "QWQ" << endl;
using namespace std;
string in, str;
int hw[MAXN + 10], mx, mid;
int main() {
cin >> in;
str += "$$";//***'s favourite
//I give *** 1145141919810 yuan away! QAQ
for(int p = 0; p < in.size(); p++) {
str += in[p], str += "$";
}
int maxn = 0;
for(int p = 1; p < str.size(); p++) {
if(p < mx) hw[p] = min(hw[mid * 2 - p], mx - p + 1);
else hw[p] = 0;
while(str[p + hw[p]] == str[p - hw[p]]) hw[p]++;
if(p + hw[p] - 1 > mx) {
mx = p + hw[p] - 1;
mid = p;
}
maxn = max(maxn, hw[p]);
}
cout << maxn - 1 << endl;
}