树分治全家桶

树，（是种在路边的绿化植物）是图论当中的一种特殊图，（由于绿化环境作用非常优秀）由于特殊性质丰富，经常出现在我们身边。

本文将主要讲述（如何植树）一种树上优美的暴力——树分治。

树分治

树分治可以将部分 \(O(n^2)\) 的暴力降至 \(O(n\log n)\) 级别，尤其适用于树上距离及其的各种变形，树上两点之间路径的问题。

Part1 点分治

处理大规模的树上路径信息问题。

点分治作为树分治的基础思想，主要利用树的重心的不断划分。

例题：P3806 【模板】点分治 1

将以此题为基础，进行讲解。

如果暴力处理每一个询问，复杂度 \(O(n^2)\)。

从树的重心入手，先找出树的重心。

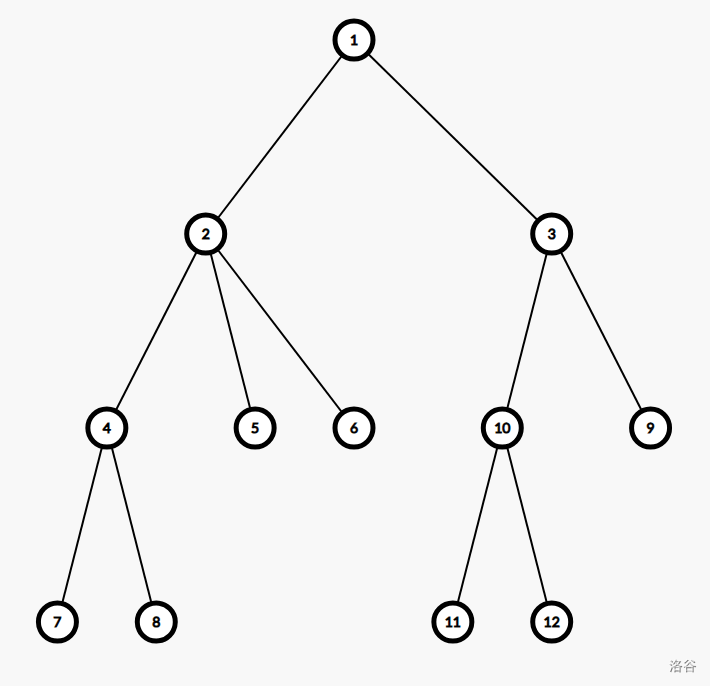
如图的树中，2 节点为树的重心。

那么以 2 为根，遍历整一棵树，求出到各个点的距离，这样就得出了以 2 为一个端点的到各个的点的距离。

我们考虑穿过 2 的一条路径，这样的路径可以由两条不在 2 的同一子树内的路径构成，将这两条路径拼起来即可（相加）。

这样子，所有穿过 2 的（包括以 2 为端点的）路径都求出来了。那么后面求的路径都和 2 无关，直接把 2 删除。

图变为：

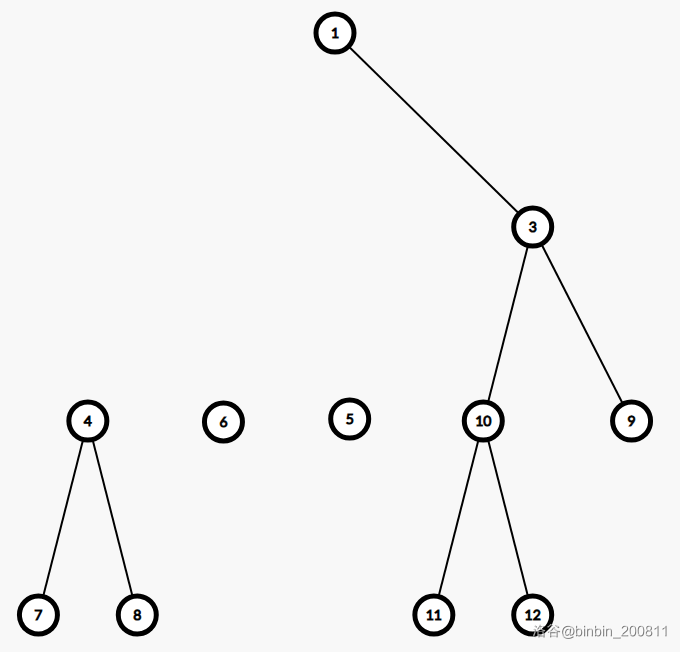
然后对于每一新树，我们在分别求出树的重心，重复上述操作，直到树中不存在节点。

对于正确性，可以发现每一条路径都寻找且只寻找了一个路径上的节点进行求路径长度，这样子，每一条路径都经过了统计，正确性可以保证。

对于时间复杂度，根据树的重心的定义，每次新的重心的最大子树大小都至少会比上次找的大小小 \(\frac{1}{2}\)，如果我们将次求出的重心向分出这棵子树的重心连边（在上图中，即节点 4、6、5、3 向 2 连边），可以发现，该树的重心的层数为 \(\log n\)，而每一层最多只会遍历一个 \(n\) 个节点，时间复杂度达到了优秀的 \(O(n\log n)\)。

例题代码：

#include<bits/stdc++.h>
using namespace std;

const int maxn=2e4+5;

struct node
{
    int to,nxt,w;
}edge[maxn*2];

int n,m,tot,sum,rt,crem;
int dis[maxn],q[maxn],rem[maxn],mx[maxn],siz[maxn],qry[maxn],head[maxn];

bool vis[maxn],jug[maxn*maxn],ans[maxn];
//vis 标记为 1 表示该点删除。
void add(int x,int y,int z)
{
    tot++;
    edge[tot].to=y;
    edge[tot].nxt=head[x];
    edge[tot].w=z;
    head[x]=tot;
}

void dfs_rt(int u,int f)//求重心
{
    mx[u]=0;
    siz[u]=1;
    for(int i=head[u];i;i=edge[i].nxt)
    {
        int v=edge[i].to;
        if(v==f||vis[v]) continue;
        dfs_rt(v,u);
        mx[u]=max(mx[u],siz[v]);
        siz[u]+=siz[v];
    }
    mx[u]=max(sum-siz[u],mx[u]);
    if(mx[rt]>mx[u]||rt==0) rt=u;
}
void dfs_dis(int u,int f)//得距离
{
    rem[++crem]=dis[u];
    for(int i=head[u];i;i=edge[i].nxt)
    {
        int v=edge[i].to;
        if(vis[v]||v==f) continue;
        dis[v]=dis[u]+edge[i].w;
        dfs_dis(v,u);
    }
}

void calc(int u)//求路径信息并合并计算，方法有部分与上述不同
{
    queue<int>que;
    while(!que.empty()) que.pop();
    for(int i=head[u];i;i=edge[i].nxt)
    {
        int v=edge[i].to;
        if(vis[v]) continue;
        crem=0,dis[v]=edge[i].w;
        dfs_dis(v,u);

        for(int j=1;j<=crem;j++)
            for(int k=1;k<=m;k++)
            {
                if(qry[k]>=rem[j]) ans[k]|=jug[qry[k]-rem[j]];
            }

        for(int j=1;j<=crem;j++) que.push(rem[j]),jug[rem[j]]=1;
    }
    while(!que.empty()) jug[que.front()]=0,que.pop();
}

void dfs(int u)//通过重心遍历树
{
    vis[u]=1;
    jug[0]=1;
    calc(u);
    for(int i=head[u];i;i=edge[i].nxt)
    {
        int v=edge[i].to;
        if(vis[v]) continue;
        sum=siz[v],rt=0;
        dfs_rt(v,0);
        dfs(rt);
    }
}

int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<n;i++)
    {
        int x,y,z;
        scanf("%d%d%d",&x,&y,&z);
        add(x,y,z);
        add(y,x,z);
    }
    for(int i=1;i<=m;i++) scanf("%d",&qry[i]);

    sum=n;
    dfs_rt(1,0);
    dfs(rt);

    for(int i=1;i<=m;i++)
    {
        if(ans[i]) printf("AYE\n");
        else printf("NAY\n");
    }
}

总结

点分治的运用一般和树上两个点有关或者树上的路径有关（一般是存在不定点）。

可以离线处理需要的树上数据。

一般通过离线将一个 \(n\) 消减为 \(\log n\)。

练习

P2634 【国家集训队】 聪聪可可

P3345 【ZJOI2015】 幻想乡战略游戏

Part2 边分治

边分治与点分治类似，不过是冷门算法。

边分治，就是针对边的分治。

选择一条边，这条边分成两边的树的大小最均匀，分别暴力处理两边树的信息，在通过边把所得的信息链接起来，就OK了。

但如果图是菊花图的话边分治会被卡成 \(O(n^2)\)。

咋办哩？

可以把原树转成一棵二叉树，像这样：

Ps：图片出处，OI-wiki树分治章节。

转成二叉树后消除了菊花图的弊端，使得边分治具有普遍性。

由于只会最多增加 \(n\) 个点，总复杂度 \(O(n\log n)\)。

点分治的题边分治也可以做大部分。

Part3 点分树

树分治的究极版本，通过改变原树形态使得层数变为 \(\log n\) 的一种重构树，通常解决与原树形态无关的带修改问题。

它牺牲了原来的结构来换取高速的结构，所以如果子树和父节点有路径（改变距离、一次性更改子树内所有节点、断开边、重连边……）关系，它就完了。

但它支持在线更改部分信息！

还记得点分治的时间复杂度证明吗？在那时，我们将次求出的重心向分出这棵子树的重心连边，证明了不超过 \(\log n\) 层的性质，现在的点分树就是利用这个连边方式，重构整棵树。

原树：

树分治后的重构树：

下面的树没有说明对于的为重构树。

一般来说，我们每一个点会存下到自己的祖先的距离，或者一些其它与祖先相关的信息，点会利用一些数据结构存下关于自己的子树内的信息。

那这种树可以干什么呢？

例题：P6329 【模板】点分树 | 震波

对于本题，可以乱搞。

距离维护一个下标关于距离前缀和（线段树/树状数组），每次改变一个点的操作，可以改变一条该点到根的路径上所有点的前缀和。

对于求值，从该节点 \(v\) 向上遍历祖先 \(x\)，求出 \(sum[x][k-dis(v,x)]\)，如果是从 \(x\) 的儿子 \(y\) 上来的，要在减去 \(sum[y][k-dis(v,x)-dis(x,y)]\)。

具体参见代码吧。

其实还有很多奇怪的技巧，比如点分治套点分树之类的……

#include<bits/stdc++.h>
using namespace std;

#define inf 1e8

const int maxn=1e5+5;

struct Edge
{
    int to,nxt;
}edge[maxn*2];
struct Tree
{
    int ct;
    int rt[maxn];
    struct node{int ch[2],val;}tree[maxn*55];
    void insert(int &p,int l,int r,int x,int y)
    {
        if(!p) p=++ct;
        if(l==r)
        {
            tree[p].val+=y;
            return ;
        }
        int mid=(l+r)>>1;
        if(x<=mid) insert(tree[p].ch[0],l,mid,x,y);
        else insert(tree[p].ch[1],mid+1,r,x,y);
        tree[p].val=tree[tree[p].ch[0]].val+tree[tree[p].ch[1]].val;
    }
    int query(int p,int l,int r,int ql,int qr)
    {
        if(ql>qr) return 0;
        if(!p) return 0;
        if(ql<=l&&r<=qr) return tree[p].val;
        if(l>qr||r<ql) return 0;
        int mid=(l+r)>>1;
        return query(tree[p].ch[0],l,mid,ql,qr)+query(tree[p].ch[1],mid+1,r,ql,qr);
    }
}w[2];

int n,tot,sum,m,rt;
int val[maxn],head[maxn],mx[maxn],siz[maxn],dis[maxn][25],fa[maxn],K[maxn];

vector<int>E[maxn];

bool vis[maxn];

void Init(int u){sum=siz[u];rt=0;}

void add(int x,int y)
{
    tot++;
    edge[tot].to=y;
    edge[tot].nxt=head[x];
    head[x]=tot;
}

void dfs_rt(int u,int f)
{
    mx[u]=0,siz[u]=1;
    for(int i=head[u];i;i=edge[i].nxt)
    {
        int v=edge[i].to;
        if(vis[v]||v==f) continue;
        dfs_rt(v,u);
        siz[u]+=siz[v];
        mx[u]=max(mx[u],siz[v]);
    }
    mx[u]=max(mx[u],sum-siz[u]);
    if(!rt||mx[u]<mx[rt]) rt=u;
}
void dfs_dis(int u,int f,int k)
{
    for(int i=head[u];i;i=edge[i].nxt)
    {
        int v=edge[i].to;
        if(vis[v]||v==f) continue;
        dis[v][k]=dis[u][k]+1;
        dfs_dis(v,u,k);
    }
}
void dfs_calc(int u,int f,int op,int st,int k)
{
    w[op].insert(w[op].rt[st],0,inf,dis[u][k],val[u]);
    for(int i=head[u];i;i=edge[i].nxt)
    {
        int v=edge[i].to;
        if(vis[v]||v==f) continue;
        dfs_calc(v,u,op,st,k);
    }
}

void build(int u)
{
    vis[u]=1;
    K[u]=K[fa[u]]+1;
    dfs_dis(u,0,K[u]);
    dfs_calc(u,0,1,u,K[u]);
    dfs_rt(u,u);
    for(int i=head[u];i;i=edge[i].nxt)
    {
        int v=edge[i].to;
        if(vis[v]) continue;
        Init(v);
        dfs_rt(v,u);
        E[u].push_back(rt);
        fa[rt]=u;
        dfs_calc(rt,u,0,rt,K[u]);
        build(rt);
    }
}

void change(int u,int st,int now)
{
    if(!u) return ;
    w[1].insert(w[1].rt[u],0,inf,dis[st][K[u]],now-val[st]);
    if(fa[u]) w[0].insert(w[0].rt[u],0,inf,dis[st][K[u]-1],now-val[st]);
    change(fa[u],st,now);
}
int dfs_ans(int u,int v,int st,int d)
{
    if(!u) return 0;
    if(d-dis[st][K[u]]<0) return dfs_ans(fa[u],u,st,d);
    int res=w[1].query(w[1].rt[u],0,inf,0,d-dis[st][K[u]]);
    if(v) res-=w[0].query(w[0].rt[v],0,inf,0,d-dis[st][K[u]]);
    return res+dfs_ans(fa[u],u,st,d);
}

void outtree(int x)
{
    cout<<x<<endl;
    for(int i=0;i<E[x].size();i++) cout<<x<<" "<<E[x][i]<<endl;
    for(int i=0;i<E[x].size();i++) outtree(E[x][i]);
}

int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++) scanf("%d",&val[i]);
    for(int i=1;i<n;i++)
    {
        int u,v;
        scanf("%d%d",&u,&v);
        add(u,v);
        add(v,u);
    }

    siz[1]=n;
    Init(1);
    dfs_rt(1,0);
    build(rt);

    int ans=0;
    for(int i=1;i<=m;i++)
    {
        int op,x,y;
        scanf("%d%d%d",&op,&x,&y);
        x^=ans,y^=ans;
        if(op)
        {
            change(x,x,y);
            val[x]=y;
        }
        else
        {
            printf("%d\n",ans=dfs_ans(x,0,x,y));
        }
    }
}

本栏目推荐文章
• DevOps常用工具全家桶，实现高效运维和交付
• [笔记]DP 全家桶
• Adobe 2023全家桶12月版本更新
• 学习Vue3 第六章（认识Ref全家桶）
• 树分治全家桶
• 重量级消息，微软将ThreadX RTOS全家桶贡献给Eclipse基金会，免费供大家商用，宽松的MIT授权方式
• 【未完善】多项式全家桶
• 苹果电脑 Adobe2023 全家桶 Mac 直装版 最新下载安装
• Adobe全家桶 2024 免费破解激活工具AdobeGenP- Win
• Adobe2024全家桶大更新， 包含Win/Mac M1 M2 ，安装教程分享

全家多项式 全家 全家vue vue3全家vue笔记 全家tarjan 全家burry 全家computed属性vue3 全家devserver参数vue3 javascript全家vue 全家request文件axios 装版 最新下载 全家 苹果