第七章：极坐标系

我们将介绍其它的用于绘制空间和位置的坐标系。这些坐标系不像笛卡尔坐标系那样「横平竖直」，所以会用到许多三角函数~~它们一定会勾起你的高中回忆~~，但它们在很多其它领域的实际问题上，能比笛卡尔坐标系表现得更好，还请重视。就来一起看看吧~

1.关于二维极坐标空间

除了笛卡尔坐标系里的\(x、y\)，还有其它方法，用同样仅两个数字来定位二维平面点的位置吗？当然有办法：

可以看到，它也有一个坐标原点，以轮盘指针的方式来描述位置，通过表示半径的 \(r\) 和表示角度的 \(\theta\)来进行定位。

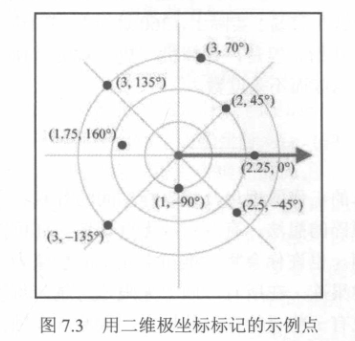
看起来不复杂，但我们在初中学习角度时就做过角度化简的题目，因此我们会想，这个角度有范围限制吗？比如上图的\((1,-90^\circ)\)可以叫\((1,270^\circ)\)吗？对于那些钝角的点像\((3,135^\circ)\)，它们的 \(r\) 算正数还是负数？
答案是：是的。一个点在极坐标中可以有多个名字，我们称这种情况为别名。
除了原点，其它的点都可以表示为\(((-1)^kr,\theta+k180^\circ)\)，\(k\)是任意的整数。当然，为了避免表达过于混乱，我们还是给出了规范坐标，它的规则如下：

不错，有这规范后就好多了。现在来谈谈二维笛卡尔坐标系和极坐标之间的变换。如果你有学过通过单位圆推导出三角函数，那接下来的变换就非常简单且熟悉了。

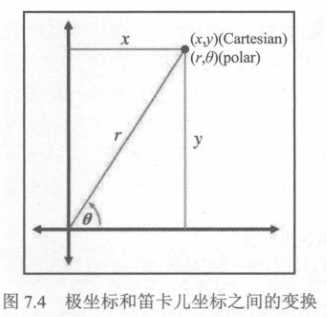
把二维笛卡尔坐标变换为极坐标：

那反过来的话：\(r=\sqrt{x^2+y^2}\)，\(\theta=\arctan(\frac{y}{x})\) 即可……吗？
对于 \(r\) 的确可以，但 \(\theta\) 如果仅仅这么求的话就会出错！一来，当 \(x=0\) 时，除法部分就有问题了；二来，\(\arctan\)得到的结果范围只有\(\begin{bmatrix}-90^\circ, +90^\circ\end{bmatrix}\)，不能规范表达原本的角度。
所以我们要人为对计算结果做科学的二次处理，本书作者将它写成了函数\(atan2(y,x)\)来替换：

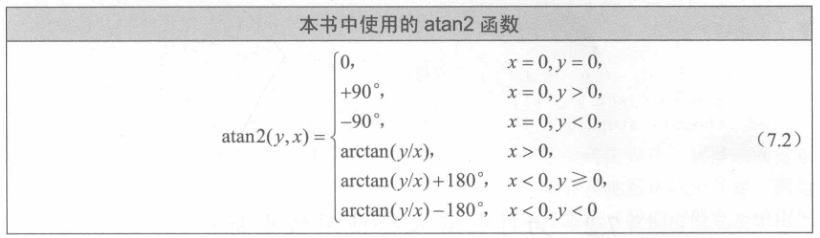
所以，最终的变换方法为：

2.为什么使用极坐标

极坐标有别名、三角函数、角度表示等问题，比笛卡尔坐标复杂多了，有什么非用不可的场合吗？
其实人类在描述位置时，往往并不使用笛卡尔坐标，比如什么“六点钟方向”、“沿东偏北45度方向走100米”……尤其是球面，我们地球的经纬网坐标就是一种三维的极坐标。
那在游戏领域呢？常见的场合是需要用到瞄准的情况，因为这通常只涉及角度，极坐标可以比笛卡尔坐标更容易使用。

3.关于三维极坐标空间

现在我们已经知道了二维极坐标算是个圆，是弯的。那三维空间中这个第三个坐标应该是直的还是弯的呢？答案是都可以。当是直的时候，整个坐标空间就是个圆柱，我们称为圆柱坐标；是弯的时候，整个坐标空间就会是个球。我们称为球面坐标。
我们先来看看比较简单的圆柱坐标：

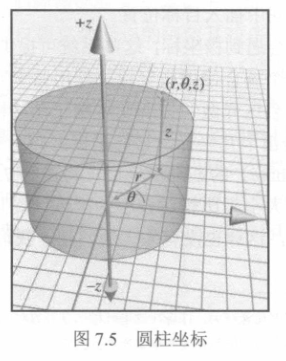
只是在原本二维极坐标的基础上加了个z，没什么好说的。至于它与三维笛卡尔坐标之间的变换，我想你也猜到了，就是在二维变换的基础上，多考虑一个z而已，z还和笛卡尔坐标中的z一样，因此可以完全不用变换它。

接下来是更常见的三维极坐标：球面坐标。

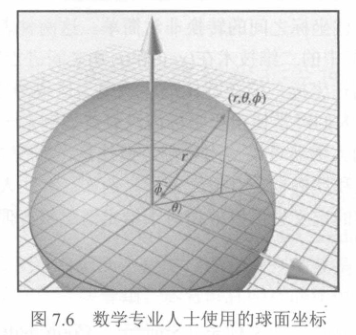
可以看出来，球面坐标在二维的基础上又多出了一个与\(z轴\)的角度 \(\phi\)。一长度两角度的表示——\((r,\theta,\phi)\)，就可以定位三维空间下的点。
这本书中，我们用右手系统。为了更容易理解，我们把水平角度 \(\theta\) 改名为 \(h\)，即航向（Heading）。垂直角度 \(\phi\)改名为\(p\)，即俯仰（Pitch）。

当然，球面坐标也有别名，我们也要做个规范球面坐标的规范。但这次的情况会比二维更复杂些，还会遇到一种叫「万向节死锁」的情况。这里就暂时提一嘴，就直接上结论吧：

那最后也来谈谈三维笛卡尔坐标和球面坐标的之间的变换吧。
首先，将三维极坐标换为笛卡尔坐标，同样借助直角三角形（不过，这次是两个），可以比较容易算出以下结果（这些结果只是对于右手规则情况的）：

接下来是由笛卡尔坐标变换为三维极坐标：