非线性规划是一种求解目标函数或约束条件中有一个或几个非线性函数的最优化问题的方法。运筹学的一个重要分支。20世纪50年代初,库哈(H.W.Kuhn) 和托克 (A.W.Tucker) 提出了非线性规划的基本定理,为非线性规划奠定了理论基础。20世纪80年代以来,随着计算机技术的快速发展,非线性规划方法取得了长足进步,在信赖域法、稀疏拟牛顿法、并行计算、内点法和有限存储法等领域取得了丰硕的成果。这一方法在工业工程、交通运输、经济管理和军事等方面有广泛的应用。

一、非线性规划实例
[资源配置问题]一容器由圆锥面和圆柱面围成。表面积为\(S\),圆锥部分高为\(h\),\(h\)和圆柱部分高\(x_2\)之比为\(a\),\(x_1\)为圆柱底圆半径,求\(x_1\)和、\(x_2\)使面积最大。
\[\begin{array}{l}
\max {\rm{ }}V = (1 + a/3)\pi x_1^2{x_2}\\
s.t.\;\left\{ {\begin{array}{*{20}{c}}
{\pi {x_1}\sqrt {x_1^2 + {a^2}x_2^2} + 2\pi {x_1}{x_2} + \pi x_1^2 = S}\\
{{x_1} \ge 0,{x_2} \ge 0\quad \quad \quad }
\end{array}} \right.
\end{array}\]

[生产管理问题] 某电视机制造厂生产二款电视机A和B。已知电视机A每月最大的销售量为500台,电视机B每月的最大销售量为400台。工厂采用随销售量增加而递减销售价格的定价方式对电视机进行定价,那么单台电视机的利润是随着销售量的增加而递减。
我们分别以\(X_A\)和\(X_B\)表示电视机A和B的月销售量,那么电视机A的销售收入可以表示为:
\[300{X_A} -\frac{150}{500}X_A^2
\]
它说明第一部A型电视机的利润为300元,最后一部(第500) 型电视机的利润为150元。电视机B的销售收入可以表示为:
\[200{X_B}-\frac{100}{400}X_B^2
\]
电视机的生产受到下下述条件限制:
装配工时限制:每月最多可供使用的工时是1200小时,而装配一台电视机A 需要2工时,装配一台电视机B需要1工时。
机器加工能力限制:每日最多可供使用的机时是1350小时,加工一台电视机A需要1机时,加工一台电视机B需要3机时。
那么,如何决定每种电视机的月产量,使月销售收入最大。
如果我们以二款电视机的月销售收入之和作为目标函数,则电视机生产管理的最优化问题被表示为:
\[\begin{array}{l}
\min \;\;S = 300{X_A} - 0.3X_A^2 + 200{X_B} - 0.25X_B^2\\
s.t.\;\;\left\{ {\begin{array}{*{20}{c}}
{2{X_A} + {X_B} \le 1200}\\
{{X_A} + 3{X_B} \le 1350}\\
{{X_A} \le 500}\\
{{X_B} \le 400}\\
{{X_A},{X_B} \ge 0}
\end{array}} \right.
\end{array}\]
[投资组合管理] 设\(x_i\),\(i=1,2, \cdot ,n\)为持有第\(i\)种证券品种的比例,满足\(\sum_{i=1}^{n}x_i=1\),\(r_i\)为第\(i\)种证券品种的收益率,\(\rho\) 为投资组合的收益率,\(Q\)为证券品种的方差-协方差矩阵,等于:
\[Q = \left[ {\begin{array}{*{20}{c}}
{{q_{11}}}&{{q_{12}}}&{ \cdot \cdot \cdot }&{{q_{1n}}}\\
{{q_{21}}}&{{q_{22}}}&{ \cdot \cdot \cdot }&{{q_{2n}}}\\
{ \cdot \cdot \cdot }&{ \cdot \cdot \cdot }&{ \cdot \cdot \cdot }&{ \cdot \cdot \cdot }\\
{{q_{n1}}}&{{q_{n2}}}&{ \cdot \cdot \cdot }&{{q_{nn}}}
\end{array}} \right]\]
数学规划模型为:
\[\begin{array}{l}
\min \;\;\sum\limits_{j = 1}^n {\sum\limits_{i = 1}^n {{q_{ij}}{x_i}{x_j}} } \\
s.t.\;\;\left\{ {\begin{array}{*{20}{c}}
{\sum\limits_{i = 1}^n {{r_i}{x_i} \ge \rho } }\\
{\sum\limits_{i = 1}^n {{x_i} = 1} }\\
{{x_i} \ge 0,i = 1,2,...,n}
\end{array}} \right.
\end{array}\]
[选址问题] 某电器制造公司的产品在\(n\)个城市中销售。为了提供优质服务,现在打算建立服务中心,希望选择地址的位置使所有城市到服务中心的距离最短。以坐标\((a,b)\) 表示服务中心的位置,设第\(i\)个城市的地址坐标为\((x_i,y_i)\),\(i=1,2,\cdot ,n\),该问题等价于找到能够覆盖所有城市半径最小的园,其几何意义见下图:
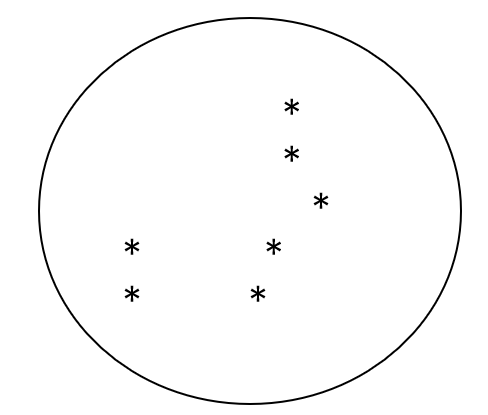
数学规划模型为:
\[\begin{array}{l}
\min \quad r\\
s.t.\quad \left\{ {\begin{array}{*{20}{c}}
{{{({x_i} - a)}^2} + {{({y_i} - b)}^2} \le r,i = 1,2,...,n}\\
{r \ge 0}
\end{array}} \right.
\end{array}\]
二、非线性规划的标准型
三、准备知识
参考文献
数学建模、运筹学之非线性规划


