526互联

有向图求强连通分量的几种算法

发布时间 2023-11-28 19:50:24作者: tianlonghuangwu

概要

本文介绍了kosaraju, tarjan算法求强连通分量

概念

有一个有向图G, 有几个概念

  1. 强连通
    若图中有两个点u和v, 他们能互相到达, 则称他们强连通
  2. 强连通图
    若是G中任意2个点都可以互相到达, 则称G是一个强连通图
  3. 强连通分量
    有向非强连通图的极大强连通子图(可以有很多个)
  4. 完全图 fully connected graph
    全部节点互相之间都有边直接连接的图

我偷懒不画图了, 理解不了的看别的博客吧
还是画个图吧, 灵魂画手来了
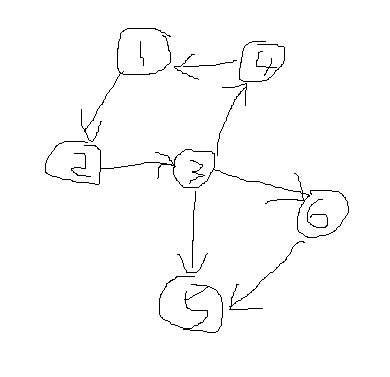
image
我们可以看出1,2,3,4互相可达, 他们是一个强连通分量
而5, 6分别也是一个强连通分量

Kosaraju算法

求这个图的强连通分量.
怎么做呢

  1. DFS一遍, 在顶点搜索完成时加入到一个栈中(其实就是逆后序"Reverse Postorder")
  2. 图每条边反转, 得到一个反图G'
  3. 栈顶取出一个节点, 若未访问过, 则在G'上进行dfs搜索, 搜索到的节点都放进一个component中
  4. 得到的component就是原图G的一个强连通分量
  5. 重复取出节点, 直至栈空

关于逆后序, 可以参考我的另一篇讲序的博客

一点粗略的小证明:
dfs(u)的过程中访问到了v节点, 提供了u->v的可达性
而反图G'中逆后序的dfs提供v->u的可达性

还有一点小证明, 逆后序是什么, 其实就是拓扑排序
所有环缩成点, 那么G会成为什么? 有向无环图
拓扑排序的功能是什么?

代码如下:

#include <bits/stdc++.h>
using namespace std;

const int SIZE = 6;
vector<std::pair<int, int>> vec = {{1, 2}, {2, 3}, {3, 4}, {4, 1}, {3, 5}, {3, 6}, {6, 5}};
stack<int> s;
bool isvisit[SIZE];
vector<vector<int>> adj(SIZE);
vector<vector<int>> adj_rev(SIZE);

void dfs(int u)
{
    isvisit[u] = true;
    for (auto pa : adj[u])
    {
        if (!isvisit[pa])
        {
            dfs(pa);
        }
    }
    s.push(u);
}

void dfs2(int u, vector<int> &component)
{
    isvisit[u] = true;
    component.push_back(u);
    for (auto pa : adj_rev[u])
    {
        if (!isvisit[pa])
        {
            dfs2(pa, component);
        }
    }
}

int main()
{
    memset(isvisit, 0, sizeof(isvisit));
    for (auto &pa : vec)
    {
        pa.first--;
        pa.second--;
        adj[pa.first].push_back(pa.second);
        adj_rev[pa.second].push_back(pa.first);
    }
    for (int i = 0; i < SIZE; i++)
    {
        if (!isvisit[i])
            dfs(i);
    }
    memset(isvisit, 0, sizeof(isvisit));
    while (!s.empty())
    {
        if (!isvisit[s.top()])
        {
            vector<int> component{};
            dfs2(s.top(), component);
            for (int i = 0; i < component.size(); i++)
            {
                cout << component[i] + 1 << " \n"[i == component.size() - 1];
            }
        }
        s.pop();
    }
    return 0;
}

输出:

1 4 3 2
6
5

tarjan

tarjan在求最大连通分量的时候, 每个点只访问一次, 每条边也只访问一次
tarjan算法维护两个数据结构
dfn[n] 时间戳
low[n] 是最低可达索引(low-link value), 表示节点可以回溯到的最早访问节点
low说人话就是, 这个节点的low值为dfs过程中, 能访问到的节点中最低的low值.
我不太会讲, 丢个讲的好的博客在这里.
博客

  1. dfs过程中只干两个事, 一个是看邻接节点有没有遍历过(看dfn就行), 第二件事是看是否在栈中, 这两种情况都要更新low
  2. dfs到结束检测 dfn[u]==low[u], 满足的话就是一个连通分量, 一直pop到栈顶元素是u为止(u当然也是连通分量里的)

具体过程是这样的
从1开始dfs
节点1的dfn为1, low为1
然后到节点2, dfn为2, low为2
继续到节点3, dfn为3, low为3
继续遍历3的邻接(4,5,6), 先到了4, 然后dfn标为4, low标为4
然后发现4相连的节点1是遍历过的, 把4的low改成为std::min(4, 1) = 1
然后继续回溯到3
然后到5, dfn标为5, low标为5
发现没有邻接, 然后进入判断, 发现节点5的dfnlow, 那么这就是一个连通分量
同理得到6是一个连通分量
最后回溯到1, 发现1的dfnlow, 那么这就是第三个连通分量

#include <bits/stdc++.h>
using namespace std;

const int SIZE = 6;
vector<std::pair<int, int>> vec = {{1, 2}, {2, 3}, {3, 4}, {4, 1}, {3, 5}, {3, 6}, {6, 5}};
stack<int> s;
vector<vector<int>> adj(SIZE);
vector<int> low(SIZE, 0);
vector<int> dfn(SIZE, 0);
vector<bool> isInStack(SIZE, false);
int dfs_num = 0;

void tarjan(int u)
{
    dfn[u] = low[u] = ++dfs_num;
    isInStack[u] = true;
    s.push(u);
    for (auto v : adj[u])
    {
        if (!dfn[v])
        {
            tarjan(v);
            low[u] = min(low[u], low[v]);
        }
        else if (isInStack[v])
        {
            low[u] = min(low[u], dfn[v]);
        }
    }
    if (dfn[u] == low[u])
    {
        vector<int> component = {u};
        while (s.top() != u)
        {
            isInStack[s.top()] = false;
            component.push_back(s.top());
            s.pop();
        }
        isInStack[u] = false;
        s.pop();
        for (int i = 0; i < component.size(); i++)
        {
            cout << component[i] + 1 << " \n"[i == component.size() - 1];
        }
    }
}

int main()
{
    for (auto &pa : vec)
    {
        pa.first--;
        pa.second--;
        adj[pa.first].push_back(pa.second);
    }
    tarjan(0);
    return 0;
}

输出:

5
6
1 4 3 2