MST(最小生成树)学习感悟
MST,最小生成树,一个有 n 个结点的连通图的生成树是原图的极小连通子图,且包含原图中的所有 n 个结点,并且有保持图连通的最少的边。——百度百科
对于最小生成树,有几个比较常见的性质:
- 对于任意最小生成树,它包含所有的n个节点以及n-1条边。
- 若边权都不相等的话,则它是唯一的。(由此可求第k小生成树)
- 最小生成树里不存在环。
对于找到最小生成树,有几个常见的算法:
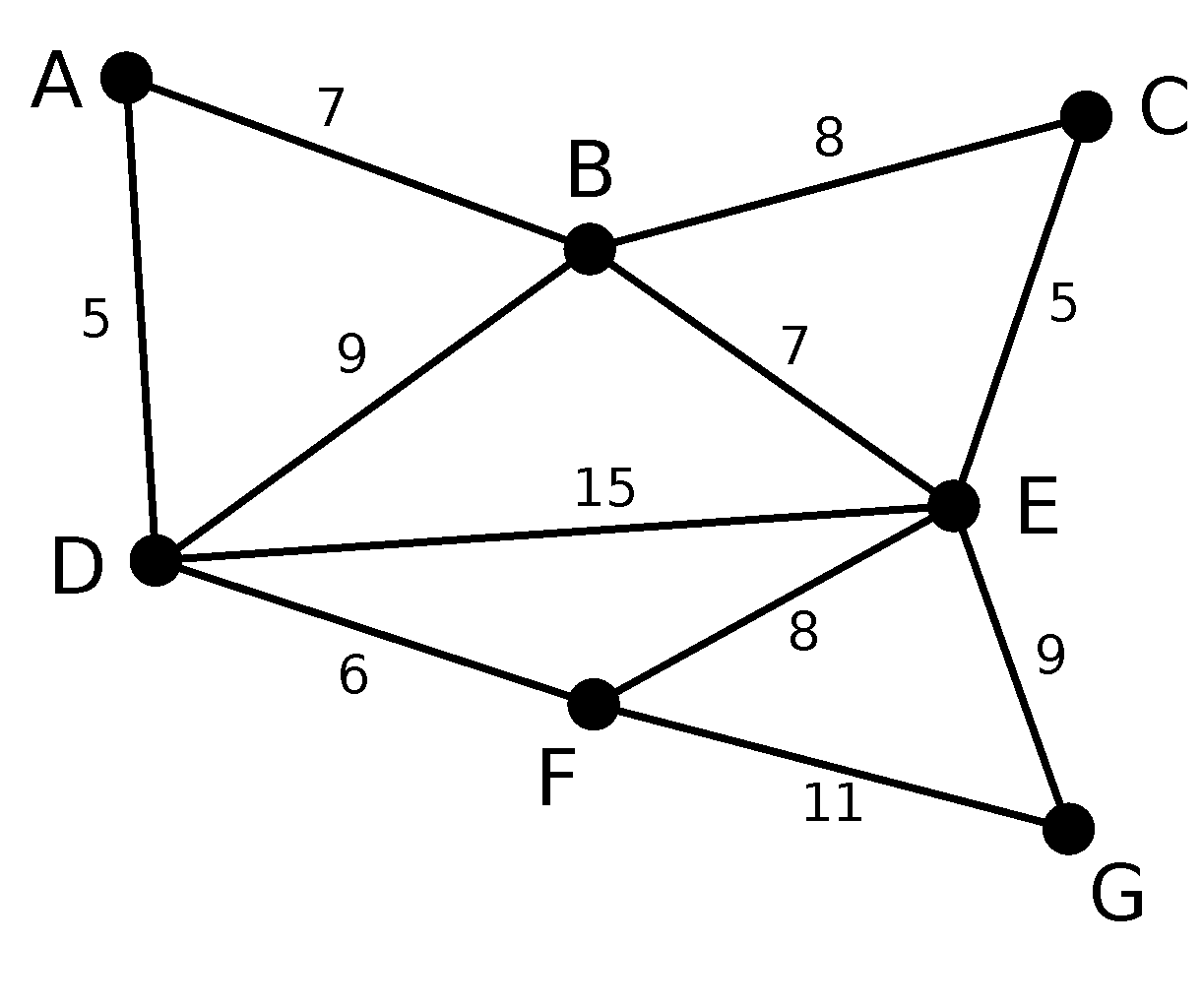
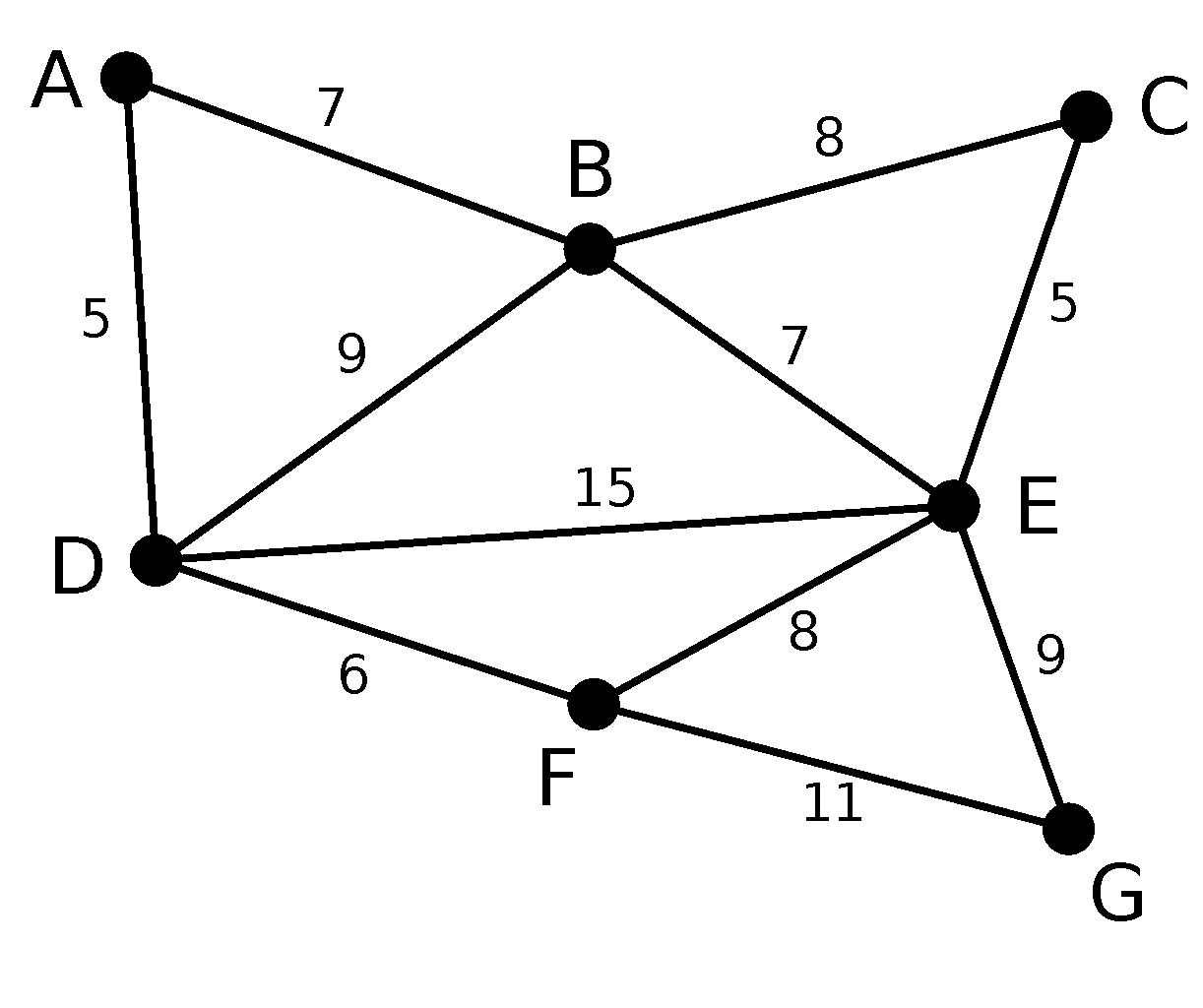
kruskal
图片来源于oi wiki(下同)
主要运用贪心思想,按边权的大小排序,时间复杂度\(O(m\, logm)\),适合用于稀疏图,通常跑的非常快,代码也较为简单。
//洛谷P3366版子 下同
#include<bits/stdc++.h>
using namespace std;
#define s(n) scanf("%d", &n)
int n, m, f[5010];
struct Edge{ int u, v, w; }e[200100];
bool cmp(Edge a, Edge b){
return a.w < b.w;
}
inline int ff(int k){
if(f[k] == k) return k;
return f[k] = ff(f[k]);
}
inline void kruskal(){
sort(e + 1, e + m + 1, cmp);
for(int i=1; i<=n; i++) f[i] = i;
int ans = 0, cnt = 0;
for(int i=1; i<=m; i++){
if(cnt == n - 1) break; //小小的优化,可要可不要
int fa = ff(e[i].u), fb = ff(e[i].v);
if(fa == fb) continue;
else{
ans += e[i].w;
cnt++;
f[fa] = fb;
}
}
if(cnt == n - 1) printf("%d", ans);
else printf("orz");
return;
}
int main(){
s(n), s(m);
for(int i=1; i<=m; i++) s(e[i].u), s(e[i].v), s(e[i].w);
kruskal();
return 0;
}
prim
prim算法是由Dijkstra发明的,并且与dijkstra最短路算法发表在同一篇论文中。prim算法与dijksrta非常像,复杂度\(O(m\,longn)\)。适合稠密图。但它跑的不一定有kruskal快。
#include<bits/stdc++.h>
using namespace std;
#define s(n) scanf("%d", &n)
int n, m, x, y, z;
struct edge{
int to, w;
edge(int a, int b){
to = a, w = b;
}
};
vector<edge> G[200001];
struct node{
int id, dis;
node(int a, int b){
id = a, dis = b;
}
bool operator < (const node &u) const{
return dis > u.dis;
}
};
bool done[5005];
inline void prim(){
int s = 1;
for(int i=1; i<=5005; i++) done[i] = 0;
priority_queue<node> q;
q.push(node(s, 0));
int ans = 0, cnt = 0;
while(!q.empty()){
node u = q.top(); q.pop();
if(done[u.id]) continue;
done[u.id] = 1;
ans += u.dis;
cnt++;
for(int i=0; i<G[u.id].size(); i++){
edge y = G[u.id][i];
if(done[y.to]) continue;
q.push(node(y.to, y.w));
}
}
if(cnt == n) printf("%d", ans);
else printf("orz");
return;
}
int main(){
s(n), s(m);
for(int i=1; i<=m; i++){
s(x), s(y), s(z);
G[x].push_back(edge(y, z));
G[y].push_back(edge(x, z));
}
prim();
return 0;
}
例题说明
它在实际运用中非常的灵活:
1.灵活选边
题目描述:
Tyvj已经一岁了,网站也由最初的几个用户增加到了上万个用户,随着Tyvj网站的逐步壮大,管理员的数目也越来越多,现在你身为Tyvj管理层的联络员,希望你找到一些通信渠道,使得管理员两两都可以联络(直接或者是间接都可以)。Tyvj是一个公益性的网站,没有过多的利润,所以你要尽可能的使费用少才可以。
目前你已经知道,Tyvj的通信渠道分为两大类,一类是必选通信渠道,无论价格多少,你都需要把所有的都选择上;还有一类是选择性的通信渠道,你可以从中挑选一些作为最终管理员联络的通信渠道。数据保证给出的通行渠道可以让所有的管理员联通。
思路
比如在联络员一题中,你需要现将必须纳入的边直接加到ans里去,然后再排序可加可不加的边,跑算法
#include<bits/stdc++.h>
using namespace std;
#define s(n) scanf("%d", &n)
int n, m, x, y, z, p, f[2010], ans=0, cnt=1;
struct edge{ int u, v, w; }e[10010];
bool cmp(edge a, edge b){ return a.w < b.w; }
inline int ff(int k){
if(f[k] != k) f[k] = ff(f[k]);
return f[k];
}
inline void kruskal(){
sort(e + 1, e + cnt, cmp);
for(int i=1; i<=cnt; i++){
int fa = ff(e[i].u), fb = ff(e[i].v);
if(fa == fb) continue;
f[fa] = fb;
ans += e[i].w;
}
printf("%d", ans);
}
int main(){
s(n), s(m);
for(int i=1; i<2010; i++) f[i] = i;
for(int i=1; i<=m; i++){
s(p), s(x), s(y), s(z);
if( p == 1){
int fa = ff(x), fb = ff(y);
f[fa] = fb;
ans += z;
}
e[cnt++] = (edge){x, y, z};
}
kruskal();
return 0;
}
2.设置虚点
题目描述
农夫约翰决定给他的N(1<=N<=300)个牧场浇水,这些牧场被自然的命名为1..N。他可以给一个牧场引入水通过在这个牧场挖一口井或者修一条管道使这个牧场和一个已经有水的牧场连接。
在牧场i挖一口井的花费是w_i(1<=w_i<=100000)。修建一条水管连接牧场i和牧场j的花费是p_ij(1<=p_ij<=100000;p_ij=p_ji;p_ii=0)。
请确定农夫约翰为了完成浇灌所有的牧场所需的最小的总花费。
思路
在挖水井中,我原先以为找到最小花费的井然后以这个井为初始点跑prim就行。但我错了,因为最小井可能不唯一,而且MST也可能不唯一。所以可以设置一个虚点,把所有井都连到这个点上去,边权为挖井的花费。用这个有n+1的图跑算法就行了。
#include<bits/stdc++.h>
using namespace std;
#define s(n) scanf("%d", &n)
int n, x, minn = INT_MAX, cnt=1, f[310];
long long ans = 0;
struct edge{
int u, v, w;
}e[900001];
bool cmp(edge a, edge b){
return a.w < b.w;
}
inline int ff(int k){
if(f[k] != k) f[k] = ff(f[k]);
return f[k];
}
inline void kruskal(){
sort(e + 1, e + 1 + n*n + n, cmp);
for(int i=1; i<=n; i++) f[i] = i;
int cnt = 0;
for(int i=1; i<=n*n+n; i++){
if(cnt == n) break;
int fa = ff(e[i].u), fb = ff(e[i].v);
if(fa == fb) continue;
f[fa] = fb;
cnt++;
ans += e[i].w;
}
printf("%lld", ans);
return;
}
int main(){
s(n);
for(int i=1; i<=n; i++){
s(x);
e[cnt++] = (edge){i, n+1, x};
e[cnt++] = (edge){n+1, i, x};
}
for(int i=1; i<=n; i++){
for(int j=1; j<=n; j++){
s(x);
if(i == j) continue;
e[cnt++] = (edge){i, j, x};
}
}
kruskal();
return 0;
}
合理调整边权
题目描述
Farmer John变得非常懒, 他不想再继续维护供奶牛之间供通行的道路. 道路被用来连接N 个牧场, 牧场被连续地编号为1..N. 每一个牧场都是一个奶牛的家. FJ计划除去P条
道路中尽可能多的道路, 但是还要保持牧场之间的连通性. 你首先要决定那些道路是需要保留的N-1条道路. 第j条双向道路连接了牧场S_j和E_j , 而且走完它需要L_j 的时间.
没有两个牧场是被一条以上的道路所连接. 奶牛们非常伤心, 因为她们的交通系统被削减了. 你需要到每一个奶牛的住处去安慰她们. 每次你到达第i个牧场的时候(即使你已
经到过), 你必须花去C_i的时间和奶牛交谈. 你每个晚上都会在同一个牧场(这是供你选择的)过夜, 直到奶牛们都从悲伤中缓过神来. 在早上起来和晚上回去睡觉的时候, 你都
需要和在你睡觉的牧场的奶牛交谈一次. 这样你才能完成你的交谈任务. 假设Farmer John采纳了你的建议, 请计算出使所有奶牛都被安慰的最少时间。
思路
安慰奶牛这道题中,根据题干n-1条边可知要求MST。通过画个草图可以知道每个边都要跑两遍,但还要考虑每个点的权值,这怎么办呢?模拟一下,在MST上,我们走每一条边时,都要加上起始点和到达点的权值,并且加边权时并不是加一次,而是要加两次。整个过程中最后一定会回到开始选择的那个点,所以还要再加一次开始点的权值。 于是每条边的边权就变成了这个样子:\(edge\_ fine[i]\, =\, begin\, +\, end\, +\, edge[i]*2\)
然后用新权值跑算法就行了。不过在跑的时候还要找到权值最小的开始点,这很简单,对吧~
#include<bits/stdc++.h>
using namespace std;
#define s(n) scanf("%d", &n)
int n, p, x, y, z, f[10001], cnt, ans=0, node[10001], mn=INT_MAX;
struct edge{ int u, v, w; }e[100010];
bool cmp(edge a, edge b){ return a.w < b.w; }
inline int ff(int k){
if(f[k] != k) f[k] = ff(f[k]);
return f[k];
}
inline void kruskal(){
for(int i=1; i<=n; i++) f[i] = i;
sort(e + 1, e + p + 1, cmp);
cnt = 0;
for(int i=1; i<=p; i++){
if(cnt == n) continue;
int fa = ff(e[i].u), fb = ff(e[i].v);
if(fa == fb) continue;
f[fa] = fb;
cnt++;
ans += e[i].w;
mn = min(mn, min(node[e[i].u], node[e[i].v]));
}
printf("%d", ans + mn);
}
int main(){
s(n), s(p);
for(int i=1; i<=n; i++) s(node[i]);
for(int i=1; i<=p; i++){
s(x), s(y), s(z);
e[i] = (edge){x, y, z * 2 + node[x] + node[y]};
}
kruskal();
return 0;
}
小数据可以打暴力~
the end