论文信息
论文标题:CDA:Contrastive-adversarial Domain Adaptation
论文作者:Nishant Yadav, M. Alam, Ahmed K. Farahat, Dipanjan Ghosh, Chetan Gupta, A. Ganguly
论文来源:2023 ArXiv
论文地址:download
论文代码:download
视屏讲解:click
1 介绍
基于域对齐的域适应方法实现了域级别的对齐,但是忽略了类级别的对齐;当源域和目标域之间的类条件数据分布存在显著差异时,可能会在类边界附近生成不明确的要素,这些要素更有可能被错误分类。
因此,本文提出了一个两阶段的领域适应模式,称为 Contrastive-adversarial Domain Adaptation (CDA)。虽然对抗性组件有助于领域级对齐,但两阶段对比学习利用类信息来实现跨领域的更高的类内紧密度,从而产生良好分离的决策边界。
2 背景

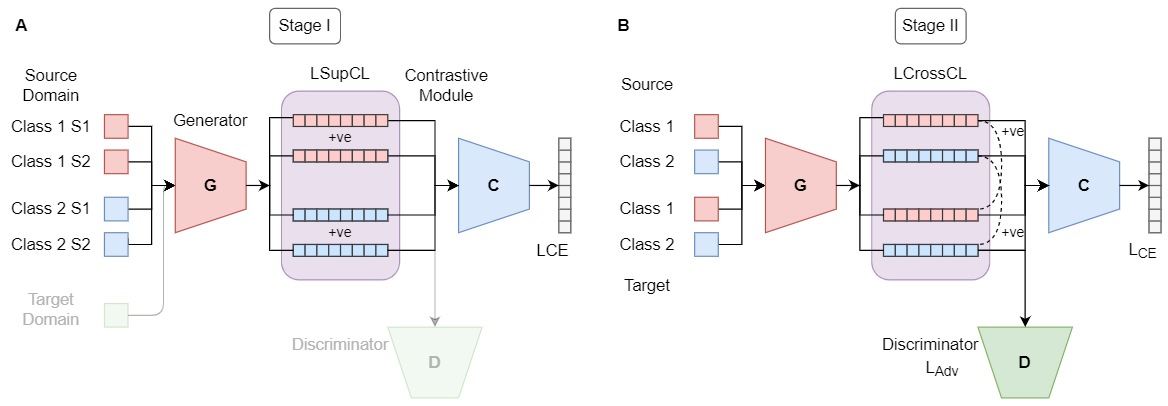
- A:基于域对抗的 UDA 在域级别对齐源和目标域,而忽略了类边界;
- B:本文方法,Step 1:CDA 在标记的源域上执行监督对比学习,从而产生更好的类内紧凑性和用于目标域对齐的良好分离的决策边界。下一步,对抗性学习导致领域级对齐,而跨域对比学习则拉动目标样本与源领域的相似样本对齐,并推开不相似的聚类;
3 方法
整体框架:
算法:

公式:
$\mathcal{L}_{\text {Adv }}\left(\mathcal{X}_{s}, \mathcal{X}_{t}\right)=\sum\limits _{\substack{\mathbf{x}_{\mathbf{s}} \sim \mathcal{X}_{s} \\ \mathbf{x}_{t} \sim \mathcal{X}_{t}}}\left(\log \left(\mathcal{D}\left(\mathcal{G}\left(\mathbf{x}_{t}\right)\right)\right)+\log \left(1-\mathcal{D}\left(\mathcal{G}\left(\mathbf{x}_{s}\right)\right)\right)\right) \quad\quad\quad(1)$
$\underset{\mathcal{G}}{\text{min}} \; \underset{\mathcal{D}}{\text{max}} \;\left(\mathcal{L}_{A d v}\right) \quad\quad\quad(2)$
$\mathcal{L}_{\text {StageI }}=\mathcal{L}_{\text {SupCL }}+\mathcal{L}_{C E} \quad\quad\quad(3)$
$\mathcal{L}_{S u p C L}\left(\mathcal{X}_{s}, \mathcal{Y}_{s}\right)=-\sum\limits _{\mathbf{z}, \mathbf{z}^{+} \in D_{s}} \log \frac{\exp \left(\mathbf{z}^{\top} \mathbf{z}^{+} / \tau\right)}{\exp \left(\mathbf{z}^{\top} \mathbf{z}^{+} / \tau\right)+\sum\limits_{\mathbf{z}^{-} \in D_{s}} \exp \left(\mathbf{z}^{\top} \mathbf{z}^{-} / \tau\right)} \quad\quad\quad(4)$
$\mathcal{L}_{\text {StageI }}=\mathcal{L}_{S \text { upCL }}+\mathcal{L}_{C E} \quad\quad\quad(5)$
$\mathcal{L}_{S u p C L}\left(\mathcal{X}_{s}, \mathcal{Y}_{s}\right)=-\sum\limits _{\mathbf{z}, \mathbf{z}^{+} \in D_{s}} \log \frac{\exp \left(\mathbf{z}^{\top} \mathbf{z}^{+} / \tau\right)}{\exp \left(\mathbf{z}^{\top} \mathbf{z}^{+} / \tau\right)+\sum_{\mathbf{z}^{-} \in D_{s}} \exp \left(\mathbf{z}^{\top} \mathbf{z}^{-} / \tau\right)} \quad\quad\quad(6)$
$\mathcal{L}_{\text {Cross } C L}\left(\mathcal{X}_{s}, \mathcal{Y}_{s}, \mathcal{X}_{t}\right)=-\sum\limits _{\substack{i=1 \\ \mathbf{z}_{s} \in D_{s} \\ \mathbf{z}_{t} \in D_{t}}}^{N} \log \frac{\exp \left(\mathbf{z}_{s}^{i \top} \mathbf{z}_{t}^{i} / \tau\right)}{\exp \left(\mathbf{z}_{s}^{i \top} \mathbf{z}_{t}^{i} / \tau\right)+\sum_{i \neq k=1}^{N} \exp \left(\mathbf{z}_{s}^{i \top} \mathbf{z}_{t}^{k} / \tau\right)} \quad\quad\quad(7)$
$\mathcal{L}_{\text {Total }}=\mathcal{L}_{\text {Stage } 1}+\mathcal{L}_{\text {Stage } 2} \quad\quad\quad(8)$
$\mathcal{L}_{\text {Total }}=\mathcal{L}_{\text {SupCL }}+\mathcal{L}_{C E}+\lambda * \mathcal{L}_{\text {Adv }}+\beta * \mathcal{L}_{\text {CrossCL }} \quad\quad\quad(9)$
$\lambda=\left\{\begin{array}{ll}0 & \text { for epoch } 0 \leq e<E^{\prime} \\\frac{2}{1+\exp ^{-\gamma p}}-1 & \text { for epoch } e \geq E^{\prime}\end{array}\right. \quad\quad\quad(10)$
$\beta=\left\{\begin{array}{ll}0 & \text { for epoch } e \leq E^{\prime \prime} \\\min \left(1, \alpha *\left(\frac{e-E^{\prime \prime}}{E^{\prime \prime}}\right)\right) & \text { for epoch } E^{\prime \prime}<e \leq E\end{array}\right. \quad\quad\quad(11)$
4 实验
可视化结果:
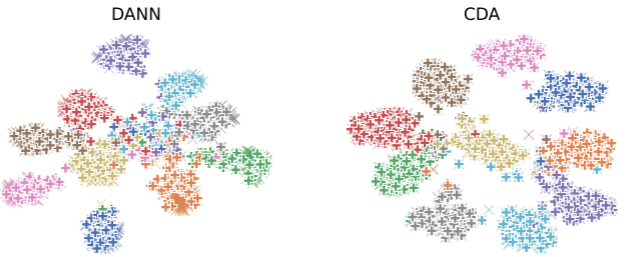
- Contrastive-adversarial Contrastive adversarial Adaptation CDAcontrastive-adversarial contrastive-adversarial contrastive adversarial domain unsupervised adversarial contrastive class-imbalanced unsupervised adversarial adaptation probabilistic contrastive adaptation learning adaptation domain moka adversarial domain unsupervised contrastive adaptation clda semi-supervised contrastive adaptation discriminative adversarial adaptation domain adaptation unsupervised contrastive network