卡特兰数 Catalan 数列
引入
有一个无限大的栈,进栈的顺序为 \(1,2,\cdots,n\),求有多少种不同的出栈序列。
设 \(h[n]\) 为 \(n\) 个数的出栈序列方案数。
可以这样想 \(k\) 是最后一个出栈的数,那么比 \(k\) 早进栈早出栈的有 \(k-1\) 个,方案数也就是 \(h[k-1]\)。同理比 \(k\) 晚进栈早出栈的方案数就是 \(h[n-k]\),那么 \(k\) 作为最后一个出栈的数贡献的方案数为 \(h[k-1]h[n-k]\)。
由于 \(1\) 到 \(n\) 中任何一个数都可以成为 \(k\),那么 \(h[n]\) 的方案数就是 \(h[n]=\sum_{i=1}^n h[i-1]h[n-i]\)。
\(h\) 就是卡特兰数列。
应用问题
-
1.有 \(2n\) 个人排队买票,票 \(5\) 元一张。有 \(n\) 个人有 \(5\) 元钞票,另外 \(n\) 个人有 \(10\) 元钞票,售票处没有其它钞票,求有多少种排队顺序不会使售票处无法找零。
分析:每一个 \(10\) 元的钞票都需要一个 \(5\) 元的钞票,不妨把 \(5\) 元看成进栈 \(10\) 元看成出栈,每一种出栈序列对应一种排队方案,问题变为引入问题,答案为 \(h[n]\)。
-
2.学校在坐标 \((n,n)\) 处,每天彬彬上学会从 \((0,0)\) 出发,向 \(x\) 轴正方向走 \(n\) 步,向 \(y\) 轴正方向走 \(n\) 步,求不穿过(可以碰到)\((n,n)\) 与 \((0,0)\) 对角线(即直线 \(y=x\))的路径数(只走直线 \(y=x\) 下方)。
分析:如果想不穿过对角线那么可以移动看做进栈和出栈。如上题,一种出栈序列对应一种路径方案,答案为 \(h[n]\)。
总结:对于一些问题,可以转换成不同出栈序列的问题,那么便可以由卡特兰数得到。
-
3.有一个 \(n\) 条边的凸多边形,用直线连接对角线,使该多边形分为多个三角形,每条直线不相交,问有多少种划分方法。
分析:我们先将多边形顺序编号 \(p_1,p_2,\cdots,p_n\),选择基边 \(p_1p_n\),再任选一个点 \(p_k\ (2\leq k \leq n-1)\),连接 \(p_1p_k,p_np_k\),这样(除连接的三角形外)将多边形重新分为了一个 \(k\) 边型和 \(n-k+1\) 边型,那么设 \(f[n]\) 为 \(n\) 边型的答案,有 \(f[n]=\sum_{i=1}^n h[i-1]h[n-i]\)。这正是卡特兰数的递推公式。
-
4.圆环上有 \(2n\) 个点,求点成对连接,线段不相交的方案数。
分析:和上述一样,选择后点对后会分为两部分,将两部分独立处理即可。
总结:如果一个问题可以通过枚举来分为两部分,通过乘法和加法原理得到相同的递推式,那么也是卡特兰数列。在做题中,我们可以先设 \(dp\) 在推式子,得出 \(dp\) 的递推公式,再来判断卡特兰数;或者先看能否分为两部分,再推式子。
公式
使用应用问题 \(2\) 推导:
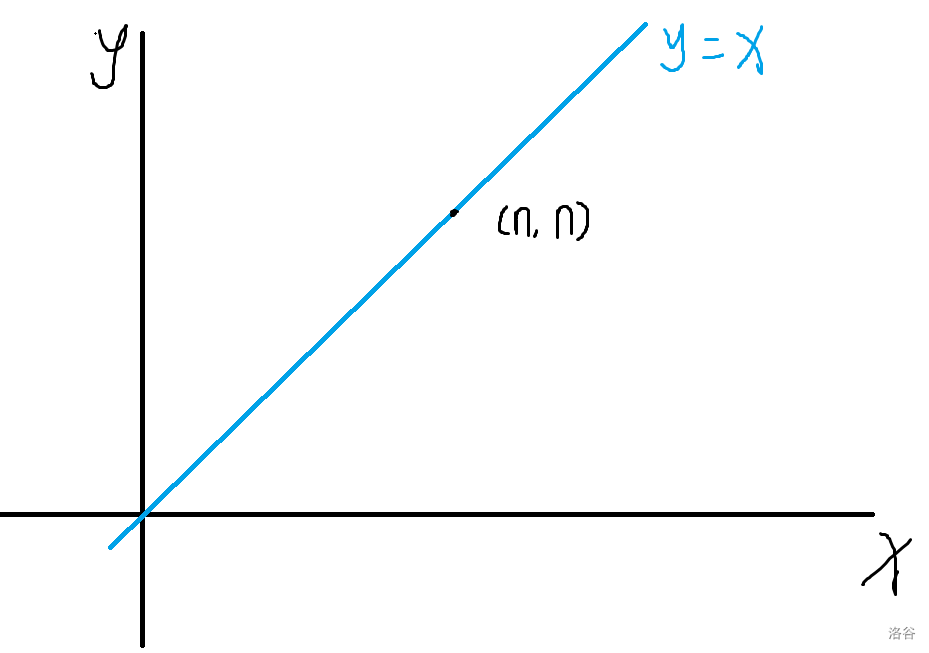
先不管不管对角线限制,从 \((0,0)\) 到 \((n,n)\) 的路径数为 \(C_{2n}^n\)。
在减去穿过对角的路径数,即减去触碰到 \(y=x+1\) 的直线的路径数。
把一条路径碰到 \(y=x+1\) 之前的路径以 \(y=x+1\) 为对称轴翻转,发现每次的起点都变成 \((-1,1)\)。

图中黄线为原触碰 \(y=x+1\) 的路径,灰色为关于 \(y=x+1\) 翻折的部分。
那么不合法线段的选择数就是从 \((-1,1)\) 走到 \((n,n)\) 的方案数。(无论怎么走都会触碰红线)
那么合法的方案数就是 \(总方案数-不合法方案数\),即 \(h[n]=C_{2n}^n-c_{2n}^{n-1}\)。
化简后变得到了 \(h[n]\) 的递推式,\(h[n]=C_{2n}^n-C_{2n}^{n-1}=\frac{C_{2n}^n}{n+1}\)。