视频来源:线性代数的本质 - 02 - 线性组合、张成的空间与基_哔哩哔哩_bilibili
线性相关 :对增加张成空间无贡献
线性无关:对增加张成空间有贡献
向量空间的一个基是张成该空间的一个线性无关的向量集。(只要能遍历空间就可以作为这个空间的基)
直观的说如果一个变换具有以下两条性质,我们就称它是线性的:
1.直线变换后依然是直线,不能弯曲
2.原点必须保持固定
如何用数值描述线性变换?
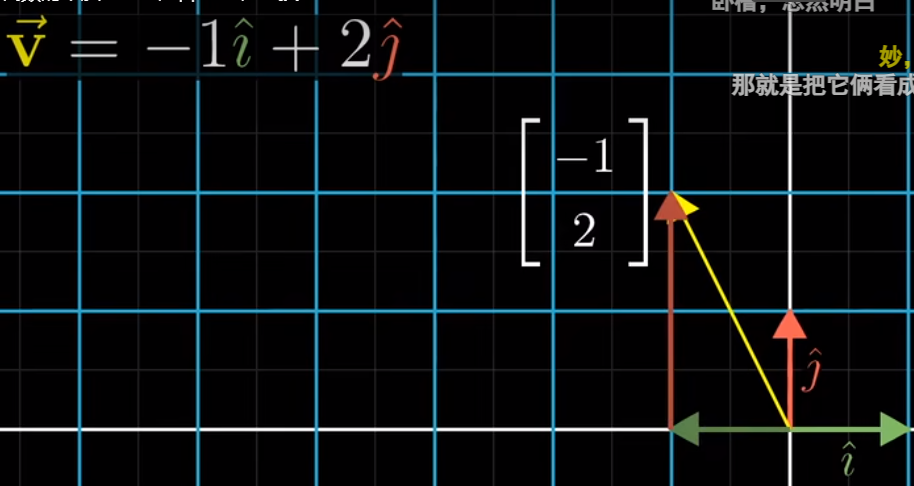

如果选择不同的基向量会怎样?每当用数字描述向量,都依赖于我们使用的基向量。两个向量标量乘法之和的结果被称为这两个向量的线性组合。
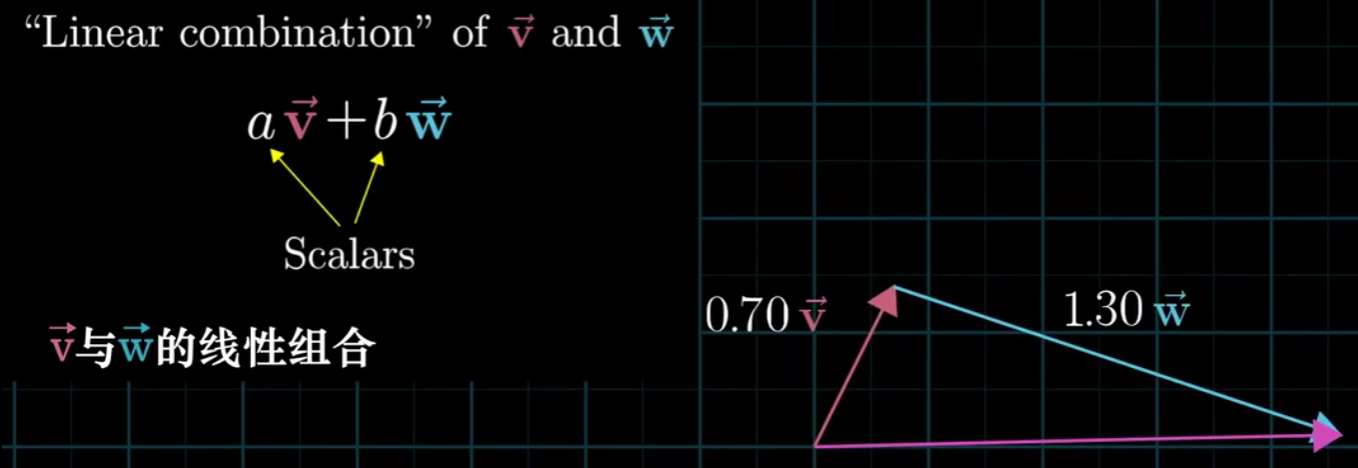
线性是哪来的?我喜欢这样理解它
如果固定一个标量,让另一个标量自由变化,所产生的向量的终点会描出一条直线
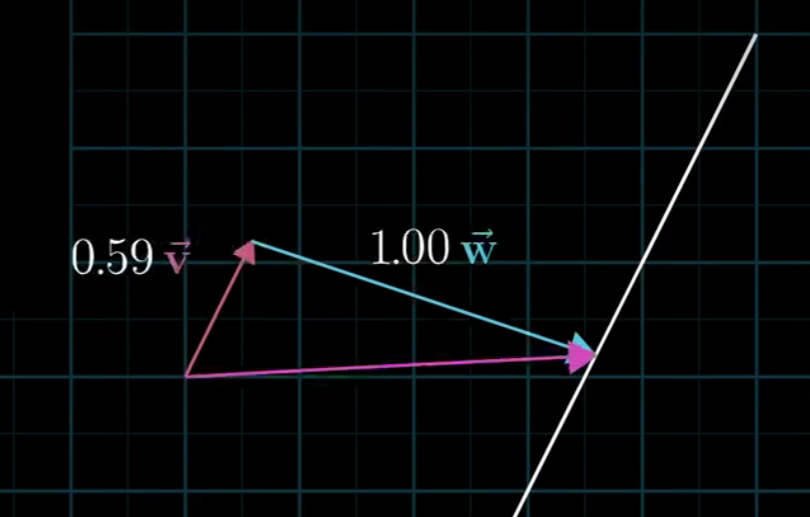
现在考虑两个标量都动,有两种情况
1.两向量不共线 能获得所有的向量
2.共线, 3 两个向量都是0向量
给定向量的张成空间:所有可以表示为给定向量线性组合的向量集合。
通常用向量的终点表示该向量。与往常一样,它的起点仍位于原点。

如果一个一组向量至少有一个是多余的,没有对张成空间做出任何贡献,你有多个向量,并且移除其中一个而不减小张成空间,当这种情况发生,我们称之为“线性相关”。
另一方面,如果所有向量都给张成的空间增加了新的维度,它们就被称为 线性无关的。
空间中的一个基的严格定义是这样的:张成该空间的一个线性无关向量的集合。
线性变换的思想与矩阵的关系:
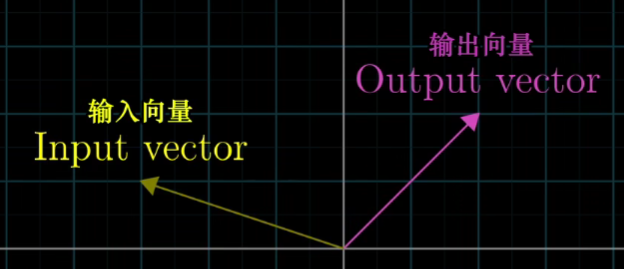
首先解析线性变换,变换本质上是函数的一种花哨的说法,接受输入内容,并输出对应结果。

在线性代数,考虑接收一个向量,并输出一个向量的变换。

既然变换和函数意义相同,为什么要用不同的术语?使用变换是在韩式以特定的方式可视化这一输入输出关系。
直观的说如果一个变换又以下两条性质,我们就称它是线性的:
1.直线变换后仍然保持为直线,不能有所弯曲 2.原点必须固定
总的来说,你应该把线性变换看作是保持网格线平行并等距分布的变换。
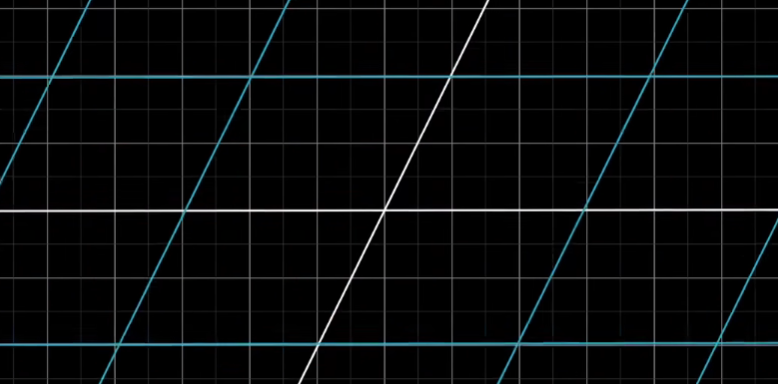
部分线性变换很容易思考,比如关于原点的旋转,

其他的稍显复杂难以言表。

你觉得该如何利用数值去描述这些线性变换呢?

实际结果是,你只需要记录两个基向量,也就是i帽和j帽变换后的位置。其他向量都会随之而动。
这个向量就是-1与i帽之积和2与j帽之积的和,
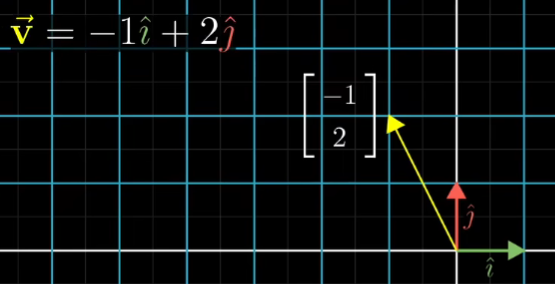
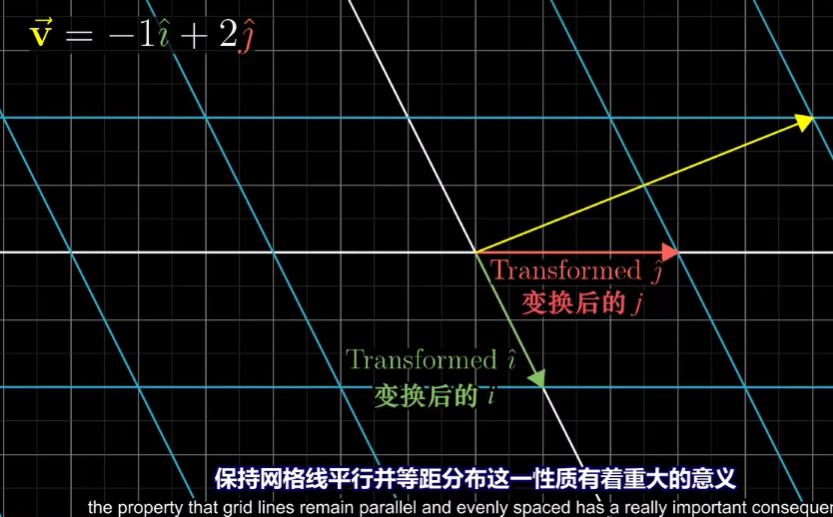
变换后也是同样的线性组合

这意味着,你可以只根据i帽和j帽的落脚点,就推断出向量v的落脚点,这也是为什么我喜欢在背景中保留原始网格的副本。
一般情况下,一个向量的坐标是(x,y),它的落脚点是x乘以i帽的落脚位置(1,-2),加上y乘以j帽的位置(3,0) ,经过运算之后你就知道它落在
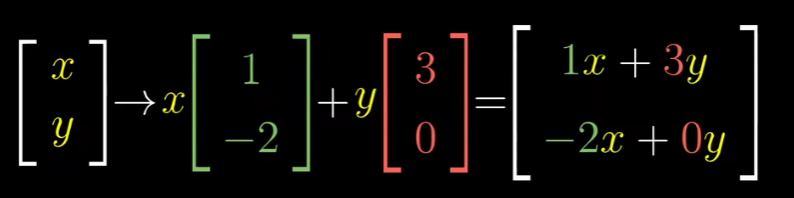
以上内容在说,一个二维线性变换仅由4个数组完全确定,变换后i帽的两个坐标与变换后j帽的两个坐标
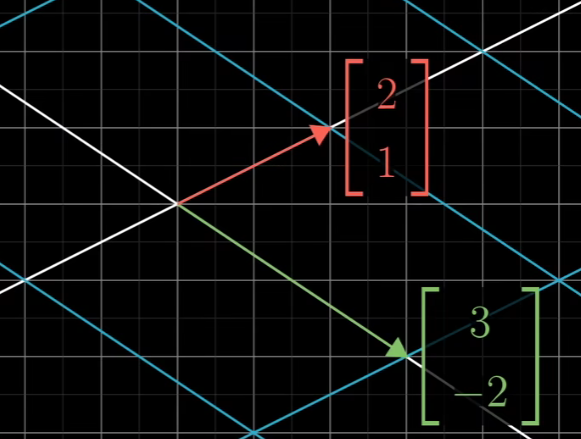
通常我们将这些坐标包装在一个2*2的格子中,称它为2*2矩阵,
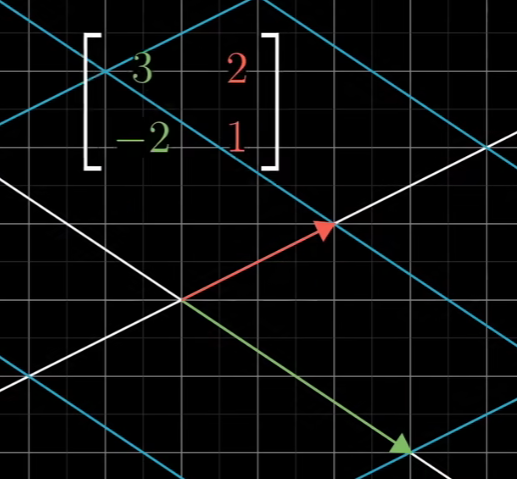
你可以把它的列理解为两个特殊的向量,即i帽和j帽分别落脚的位置
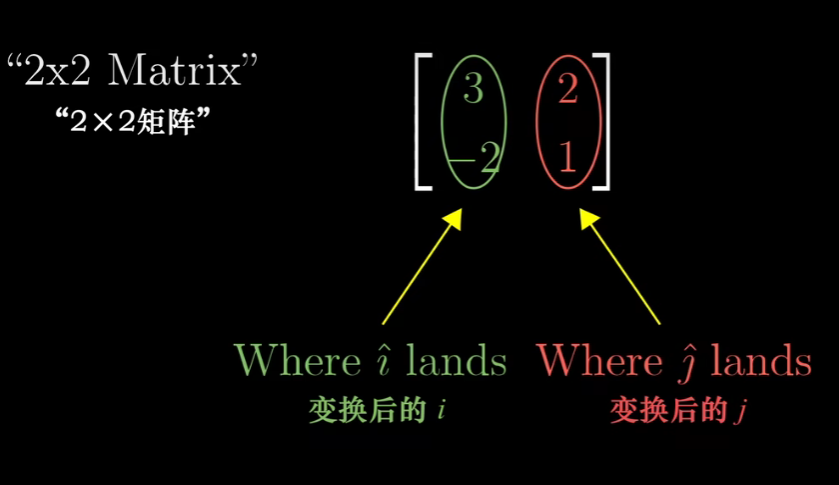
如果你有一个描述线性变换的2*2矩阵,以及一个给定向量,你想了解线性变换对这个向量的作用,
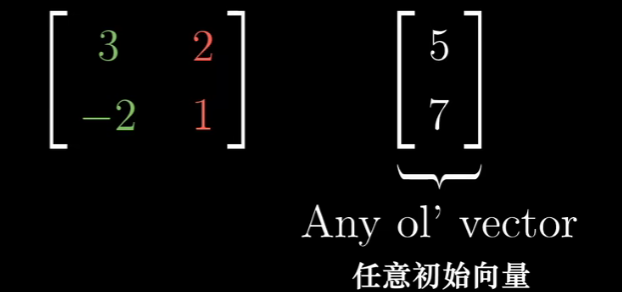
你只需要取出向量的坐标,将它们分别与矩阵的特定列相乘,然后将结果相加即可。
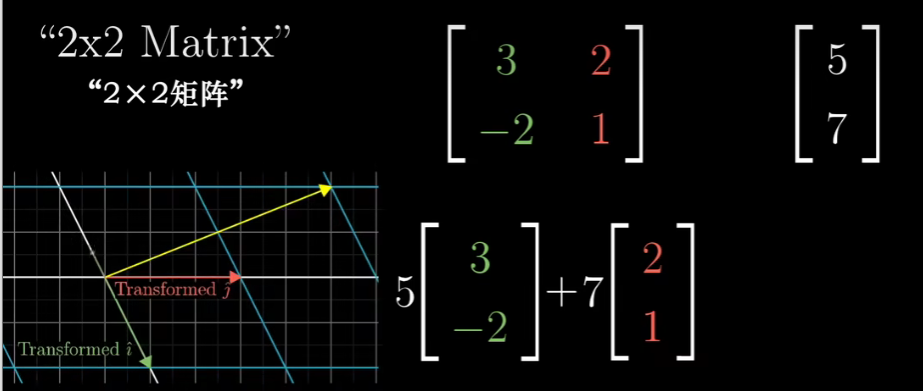
这与“缩放基向量再相加”的思想一致。
更一般的情况下,我们来看看矩阵[[a,b],[c,d]]时会发生什么
记住,矩阵在这里知识一个记号,它描述一个线性变换的信息,把第一列(a,c)看作是第一个基向量的落脚点,第二列(b,d)看作是第二个基向量的落脚点,

我们把这个而变换作用域向量(x,y) 结果是什么? 那就应该是
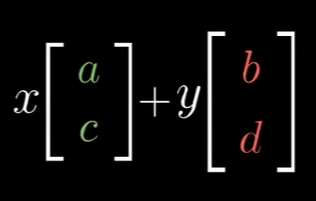
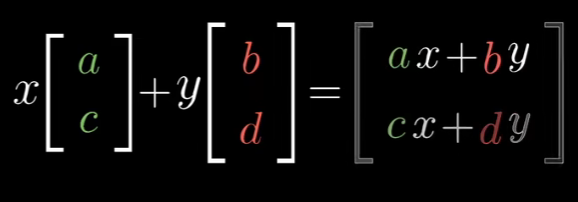
你甚至可以把它定义为矩阵向量乘法,
把矩阵向量乘法看作一个线性组合,这样想更有意思。
接下来我们练习用矩阵描述一些线性变换,比如说我们将整个空间逆时针旋转90度,那么i帽落在坐标
(0,1)上,j帽落在(-1,0)上,那么这个矩阵的列分别是(0,1)和(-1,0)

如果向算出任意向量再逆时针旋转90度后的位置,你只需要把它与矩阵相乘即可,
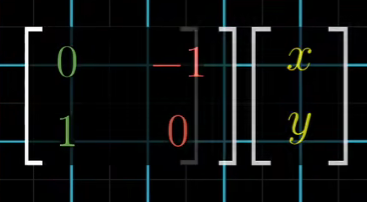
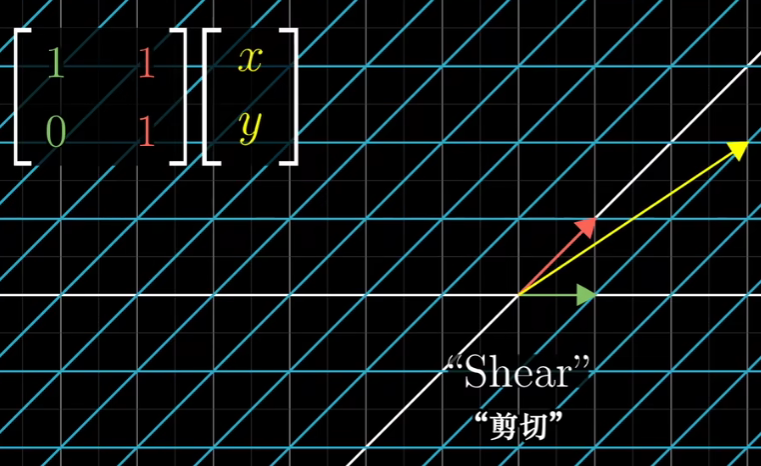
这里还有一个有趣的变换,它有个特殊的名字叫剪切,
在这个变换里 i帽保持不变,
反过来看又会如何,从一个矩阵除法,比如说一个以(1,2)和(3,1)为列的矩阵,你想推测出它代表的线性变换是什么样?
如果变换后的i帽和j帽是线性相关的,

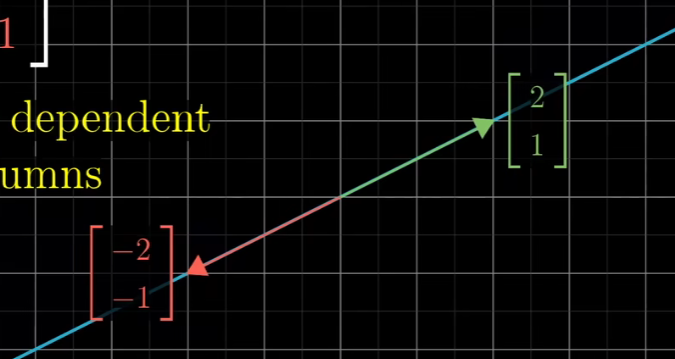
那么这个线性变换将整个二维空间挤压到它们所在一条直线上,
总之 线性变换是操纵空间的一种手段,它保持网格线平行并等距分布,并且保持原点不动,
以这些坐标为列构成的矩阵为我们提供了一种描述线性变换语言,
这里重要的一点是,每当你看到一个矩阵时,你都把它解读为对空间的一种特定变换。