题目
点这里看题目。
对于一个长度为 \(m\) 的、由互不相同整数组成的序列 \(a\),其为“连续”的当且仅当 \(\max a-\min a=m-1\),也即 \(a\) 的值构成整数上一个连续的区间。
给定正整数参数 \(n\),有 \(T\) 次询问。每次询问给出一个长度为 \(n\) 的正整数序列 \(L\),你需要求出满足下列条件的 \(1\sim n\) 的排列 \(p\) 的个数:
- 对于任意的 \(1\le r\le n\),\(p\) 以 \(r\) 结尾的“连续”区间的最大长度为 \(L_r\)。
答案对 \(998244353\) 取模。注意可能不存在符合条件的排列。
所有数据满足 \(1\le T\le 100, 1\le n\le 5\times 10^4\)。
分析
首先研究一下“连续”区间的性质:如果 \(I_1=[l_1,r_1]\) 和 \(I_2=[l_2,r_2]\) 是“连续”区间,且 \(I_1\cap I_2\neq \varnothing\),则 \(I_1\cup I_2\) 与 \(I_1\cap I_2\) 都是“连续”区间。
这说明,集合 \(\{[r-L_r+1,r]|1\le r\le n\}\) 中的两个区间要么包含,要么不交,那么一定会产生树形结构。
所以,如果 \(L_n\neq n\),或者区间之间不形成树形结构,答案就是 \(0\)。否则,一定可以构造出符合条件的排列。
我们进一步观察计数方法。首先考虑 \([1,n]\) 下面的儿子区间:
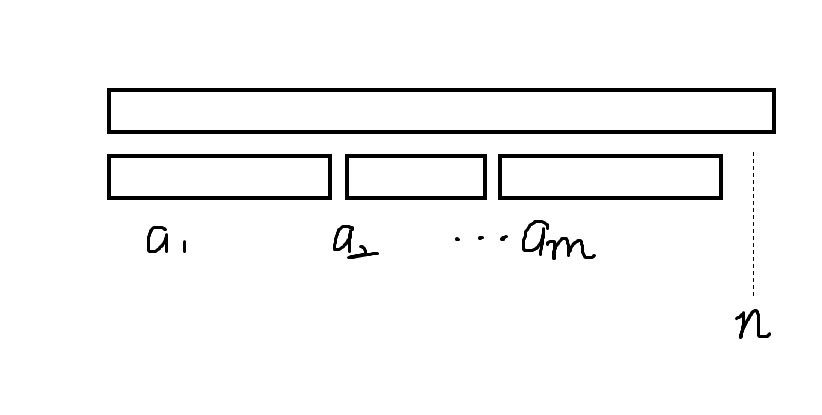
假如有 \(m\) 个儿子,长度分别为 \(a_1,a_2,\dots,a_m\),子树内部的方案数分别为 \(c_1,c_2,\dots,c_m\)。每个儿子区间对应的值区间均连续,因此我们仅需要考虑儿子的值区间的相对大小关系。当我们考虑跨儿子的区间时,首先肯定要求任意一段儿子区间并起来后不“连续”;其次,该条件满足后,可以证明不存在跨儿子区间的“连续”区间。那么,这一部分的方案数,就应该等于“令 \(n=m+1\),\(L_{m+1}=m+1\) 且 \(\forall 1\le i\le m,L_i=1\) 时,原问题的答案”,记其为 \(g_m\)。于是,此处答案就是 \(g_m\prod_{k=1}^mc_k\)。
注意到儿子的结构完全同构于 \([1,n]\) 处的结构。因此记 \(s_r\) 为区间 \([r-L_r+1,r]\) 下的儿子个数,答案就是 \(\prod_{r=1}^ng_r\)。
现在着力计算 \(g\)。我们注意到刚刚的讨论给出了一个递归构造排列的过程。设 \(F(x)=\sum_{n\ge 1}n!x^n\),也即非空排列的 OGF。那么,根据上述构造,我们可以知道 \(n!=[x^{n-1}]\sum_{m=0}^{n-1}g_mF(x)^m\)(对于 \(n\ge 1\))。于是,设 \(G(x)=\sum_{m\ge 0}g_mx^m\),我们不难得到复合方程:
进一步地,改写成 \(x=\frac{F(x)}{G[F(x)]}\) 的形式,我们可知 \(H=\frac{x}{G}\) 为 \(F\) 的复合逆。此时就可以导出一个 \(O(n^2)\) 的算法。
你说得对,但是常数小估计也过不去。
复合方程很难处理,我们尝试转化成熟悉的微分方程的形式。
怎么下手呢?对于 \(G\) 直接求导只会让人更加困惑,并且丢掉了“复合”的联系。同时,我们注意到 \(F\) 有一个很简洁的微分方程(然而不是我注意到的):
能不能从它入手给出 \(G\) 的微分方程呢?Positive! 以下是详细推导:
Remark.
对于变量间关系要有这样的理解......对于 OIer 来说还是太超前了一点 ?。
提取第 \(n\) 项系数,我们得到:
整理可得递推式:
做分治 NTT 即可(注意这是在线卷积)。复杂度为 \(O(n\log^2n+nT)\)。
代码
#include <bits/stdc++.h>
#define rep( i, a, b ) for( int i = (a) ; i <= (b) ; i ++ )
#define per( i, a, b ) for( int i = (a) ; i >= (b) ; i -- )
const int mod = 998244353;
const int MAXN = ( 1 << 17 ) + 5;
template<typename _T>
inline void Read( _T &x ) {
x = 0; char s = getchar(); bool f = false;
while( s < '0' || '9' < s ) { f = s == '-', s = getchar(); }
while( '0' <= s && s <= '9' ) { x = ( x << 3 ) + ( x << 1 ) + ( s - '0' ), s = getchar(); }
if( f ) x = -x;
}
template<typename _T>
inline void Write( _T x ) {
if( x < 0 ) putchar( '-' ), x = -x;
if( 9 < x ) Write( x / 10 );
putchar( x % 10 + '0' );
}
int P[MAXN], Q[MAXN], g[MAXN];
int lim[MAXN];
int N;
inline int Qkpow( int, int );
inline int Inv( const int &a ) { return Qkpow( a, mod - 2 ); }
inline int Mul( int x, const int &v ) { return 1ll * x * v % mod; }
inline int Sub( int x, const int &v ) { return ( x -= v ) < 0 ? x + mod : x; }
inline int Add( int x, const int &v ) { return ( x += v ) >= mod ? x - mod : x; }
inline int& MulEq( int &x, const int &v ) { return x = 1ll * x * v % mod; }
inline int& SubEq( int &x, const int &v ) { return ( x -= v ) < 0 ? ( x += mod ) : x; }
inline int& AddEq( int &x, const int &v ) { return ( x += v ) >= mod ? ( x -= mod ) : x; }
inline int Qkpow( int base, int indx ) {
int ret = 1;
while( indx ) {
if( indx & 1 ) MulEq( ret, base );
MulEq( base, base ), indx >>= 1;
}
return ret;
}
namespace Basics {
const int g = 3, phi = mod - 1, L = 17;
int w[MAXN];
inline void NTTInit( const int &n = 1 << L ) {
w[0] = 1, w[1] = Qkpow( g, phi >> L );
rep( i, 2, n - 1 ) w[i] = Mul( w[i - 1], w[1] );
}
inline void DIF( int *coe, const int &n ) {
int *wp, p, e, o;
for( int s = n >> 1 ; s ; s >>= 1 )
for( int i = 0 ; i < n ; i += s << 1 ) {
p = ( 1 << L ) / ( s << 1 ), wp = w;
for( int j = 0 ; j < s ; j ++, wp += p ) {
e = coe[i + j], o = coe[i + j + s];
coe[i + j] = Add( e, o );
coe[i + j + s] = Mul( *wp, Sub( e, o ) );
}
}
}
inline void DIT( int *coe, const int &n ) {
int *wp, p, k;
for( int s = 1 ; s < n ; s <<= 1 )
for( int i = 0 ; i < n ; i += s << 1 ) {
p = ( 1 << L ) / ( s << 1 ), wp = w;
for( int j = 0 ; j < s ; j ++, wp += p )
k = Mul( *wp, coe[i + j + s] ),
coe[i + j + s] = Sub( coe[i + j], k ),
coe[i + j] = Add( coe[i + j], k );
}
std :: reverse( coe + 1, coe + n );
int inv = Inv( n ); rep( i, 0, n - 1 ) MulEq( coe[i], inv );
}
}
void Divide( const int &l, const int &r ) {
if( l == r ) {
if( l == 0 ) g[l] = 1;
else SubEq( g[l], Mul( l - 3, g[l - 1] ) );
return ;
}
int mid = ( l + r ) >> 1, L;
Divide( l, mid );
if( l == 0 ) {
for( L = 1 ; L <= mid * 2 ; L <<= 1 );
rep( i, 0, L - 1 ) P[i] = Q[i] = 0;
rep( i, 1, mid ) P[i] = Mul( i - 1, g[i] ), Q[i] = g[i];
Basics :: DIF( P, L ), Basics :: DIF( Q, L );
rep( i, 0, L - 1 ) MulEq( P[i], Q[i] );
Basics :: DIT( P, L );
rep( i, mid + 1, r ) AddEq( g[i], P[i] );
} else {
for( L = 1 ; L <= ( r - l ) + ( mid - l ) ; L <<= 1 );
rep( i, 0, L - 1 ) P[i] = Q[i] = 0;
rep( i, l, mid ) P[i - l] = Mul( i - 1, g[i] );
rep( i, 1, r - l ) Q[i] = g[i];
Basics :: DIF( P, L ), Basics :: DIF( Q, L );
rep( i, 0, L - 1 ) MulEq( P[i], Q[i] );
Basics :: DIT( P, L );
rep( i, mid + 1, r ) AddEq( g[i], P[i - l] );
rep( i, 0, L - 1 ) P[i] = Q[i] = 0;
rep( i, l, mid ) P[i - l] = g[i];
rep( i, 1, r - l ) Q[i] = Mul( i - 1, g[i] );
Basics :: DIF( P, L ), Basics :: DIF( Q, L );
rep( i, 0, L - 1 ) MulEq( P[i], Q[i] );
Basics :: DIT( P, L );
rep( i, mid + 1, r ) AddEq( g[i], P[i - l] );
}
Divide( mid + 1, r );
}
inline int Calc( const int &l, const int &r ) {
if( lim[r] != r - l + 1 ) return 0;
if( l == r ) return 1;
int res = 1, cnt = 0;
for( int i = r - 1 ; i >= l ; ) {
if( lim[i] > i - l + 1 ) return 0;
MulEq( res, Calc( i - lim[i] + 1, i ) );
cnt ++, i = i - lim[i];
}
return Mul( res, g[cnt] );
}
int main() {
Basics :: NTTInit();
int T; Read( T ), Read( N );
Divide( 0, N - 1 );
while( T -- ) {
rep( i, 1, N ) Read( lim[i] );
Write( Calc( 1, N ) ), putchar( '\n' );
}
return 0;
}