来感受一下 IOI 的题目质量。
没做 T6。
CF436E Cardboard Box
tag:选数问题的调整方法,贪心
考虑如果我们把一个数两个都选,那么根据简单调整法,显然不存在 \(b_i\) 比它小的数一个都没选。所以假设我们枚举选了两次的 \(b_i\) 最大的数,那么它前面都选了至少一次,后面都选了至多一次,所以问题变成了一个最多只能选一个的问题了,此时只需要找到前 \(k\) 小,使用树状数组二分即可。
loj3988. 「IOI2023」封锁时刻
\(\mathcal{O}(n^2)\) 就是设 \(f_{i,j,0/1,0/1}\),表示 \(i\) 子树选了 \(j\) 个点,与 \(X/Y\) 是否联通的最小花费。
然后先处理掉两个点可达的点不交的情况,然后强制 \(X\to Y\) 路径上的所有点都选,此时发现离 \(X,Y\) 更远的点会延后被选,而路径上的限制为 \(1\),所以直接做 Cardboard Box 是对的(由于越靠近中间的点权值越小,所以选的肯定是中间的一个区间)
loj3989. 「IOI2023」最长路程
tag:构造,交互(3 increase 2)
先说一下 \(D=1\) 的情况下,已知图的情况下如何维护出最长路。
仿照证明竞赛图有哈密顿路的方式,动态维护路径,每次插入一个点。先考虑它能否接到链的首尾,如果不能那么首尾一定有边,此时随便找一条边连到环上就可以构造出来链了。
考虑减一下操作次数。维护当前所有联通块,然后二分找到当前点连的哪个联通块,然后二分找边,可以得到 \(\mathcal{O}(n\log n)\) 的操作次数。
此时应用常规的优化思路已经无法取得进展,考虑继续寻找图的性质。可以发现,假如图有超过 \(1\) 个联通块,那么一定是两个联通块的完全图,证明不难。
所以我们只需要维护两条链,甚至都没必要维护联通情况。维护两条链的链首 \(s_1,s_2\),那么每次插入一个点 \(u\),可以得到如下算法:
- 询问 \(u\) 与 \(s_1\) 是否有边,如果有,连边 \((u,s_1)\)。
- 否则,询问 \(u\) 与 \(s_2\) 是否有边,如果有,连边 \((u,s_2)\)。
- 否则,连边 \((s_1,s_2)\),并令 \(u\) 为单独的链。
最后需要判断两条链是否联通,如果联通,需要找两条链之间的一条边。
操作次数约为 \(2n+2\log n\)。
考虑进一步优化,注意到 \(1.5n\leq 400\),所以可以尝试三次操作插入两个点,讨论是 trivial 的,此处略去。
类似的题:CF1705F。
loj3990. 「IOI2023」足球场
tag:DP,优化状态,类最大子矩形问题
先考虑怎么判断合法。
首先可以发现,如果行的连续段 \(>1\),那么一定不合法,列同理。
那么它是不是充分的呢?不是,发现行的区间关系只能是包含,不能不包含但相交。
那么它是不是充分的呢?不是,发现如果两个大的把中间夹起来也是不合法的。
所以可以得出这样一个结论:区间相互包含,且单峰。
处理单峰的方式是经典的。枚举最中间的行,然后设 \(f_{i,j,l,r}\) 表示行区间 \([i,j]\),且最后一个放的区间为 \([l,r]\),最大的矩形面积是多少。转移容易做到 \(\mathcal{O}(n^4)\)。
试图使用贪心性质调整来优化是困难的。不过实际上这个状态设计有相当多的瑕疵,因为很多状态都被重复表示了,我们需要减少重复。发现如果确定了“中轴线”,那么已知行区间 \([i,j]\) 的话,那么 \([l,r]\) 显然是穿过中轴线的每行区间的交。所以可以少记录一维状态,优化到 \(\mathcal{O}(n^3)\)。
然后 \(\mathcal{O}(n^2)\) 很智慧。我们直接用一个矩形中的位置来表示一个矩形,其表示的矩形为它到它上面第一个障碍的矩形,其最大面积。转移仍然是两类:
- 在末尾加入,此时 \(f_{i,j}\) 由 \(f_{i-1,j}\) 转移过来。
- 在开头加入,那么可以找到最后一次缩小的位置,它一定是 \((i,j)\) 在行上对应区间的左端点或者右端点上面的障碍点,所以可以从 \(f_{i,pre_{i,j}}\) 和 \(f_{i,nxt_{i,j}}\) 转移过来。
总时间复杂度为 \(\mathcal{O}(n^2)\)。
loj3991. 「IOI2023」山毛榉树
tag:充要条件的推导,感性猜测与理性证明
建议配合官方讲题视频食用。
这是一道推结论题,我们尝试先寻找一些合法子树的性质,即必要条件,然后逐步加强限制,使得条件充分。
对于每种颜色 \(c\) 单独考虑,可以发现:
- 存在子结点使得子结点到父亲的边的颜色为 \(c\) 的结点为序列 \(\{v_i\}\) 的一个前缀。
- 不存在一个结点,使得同时存在两个子结点,它们到父亲的边都为 \(c\)。
上述结论由定义立得。
第二个条件是容易判断的,下面我们默认其被满足。对第一个条件做一个转述:考虑 \(\text{col}_u\) 表示 \(u\) 的儿子的颜色构成的集合,那么对于任意两个节点 \(u,v\),那么满足 \(\text{col}_u\subseteq \text{col}_v\),要么满足 \(\text{col}_v\subseteq \text{col}_u\)。
那么这个条件是否充分呢?实际上,枚举可以得到满足这个条件却不合法的反例:
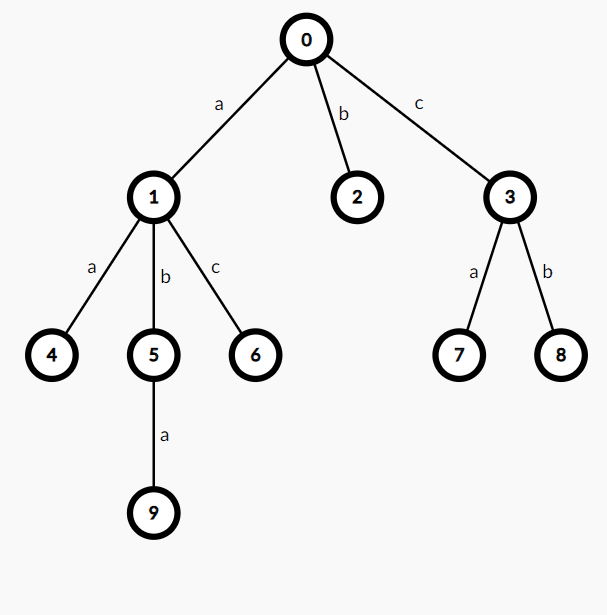
可以发现,\(2\) 号结点为 \(\{v_i\}\) 中首个出现的颜色为 \(\texttt{b}\) 的结点,其在 \(\{v_i \}\) 中的编号比 \(5\) 号结点小,而 \(2\) 号结点没有颜色为 \(\texttt{a}\) 的儿子,所以 \(9\) 号结点应该接在 \(2\) 号结点而非 \(5\) 号结点。
所以需要加强限制。我们引入概念“子树包含”:称以 \(u\) 为根的子树 \(T_u\) 包含以 \(v\) 为根的子树 \(T_v\)(\(T_v\subseteq T_u\)),当且仅当可以通过在 \(T_v\) 上不断添加叶子使得其与 \(T_u\) 同构。我们断言,子树合法当且仅当对于任意两个节点 \(u,v\),要么满足 \(T_u\subseteq T_v\),要么满足 \(T_v\subseteq T_u\)。
这样似乎非常自然:因为添加节点 \(u\) 时,我们会优先将其添加到序列 \(\{v_i\}\) 中编号小的结点的下面,而这恰好是子树较大的结点。下面我们分别证明其必要性和充分性:
- 必要性:假设条件不成立,我们通过模拟添加的过程证明它一定不合法。如果存在 \(u,v\),使得 \(T_u,T_v\) 交叉而无包含关系,不妨设 \(u\) 是在 \(\{v_i\}\) 中更加靠前的结点,那么在正常的加入顺序中,\(u\) 的颜色 \(c\) 对应的出边的终点一定比 \(v\) 的颜色 \(c\) 对应的出边的终点更加靠前,这是因为对于相同的颜色 \(c\),我们总是选择位置最靠前的结点连接。由于 \(T_v\nsubseteq T_v\),我们找到多出来的节点 \(v'\),那么 \(v'\) 显然应该接在 \(u\) 子树中对应位置上,因为编号更小。
- 结合上面的例子理解,\(T_1\) 中多出的 \(9\) 号结点,应该接在 \(T_0\) 的对应位置 \(2\) 上。
- 充分性:我们说明满足条件的子树一定存在对应的排列。构造排列是简单的,我们只需要根据包含关系一一加入即可。关键在于,我们需要证明不存在调整的方法使得当前加入的结点 \(u\) 能接到编号更小的结点上。假设 \(u\) 上的边的颜色为 \(c\),等价于说明任意位置比 \(\text{fa}_u\) 靠前的结点都存在颜色为 \(c\) 的出边。而根据之前的分析,比 \(\text{fa}_u\) 靠前的结点的 \(c\) 的出边对应的子树一定完全包含 \(u\) 的子树,其出现位置一定比 \(u\) 靠前,所以在 \(u\) 加入之前,所有的结点都被占用,所以 \(u\) 只能接到 \(\text{fa}_u\) 上。
综上我们证明了结论,下面是如何实现。关键在于判断子树之间的包含关系,实际上,依据 \(sz_u\) 排序已经可以得到最终的序列,我们只需要判断排序后相邻的两个节点是否互相包含,而判断是否包含只需要判断 \(\text{col}_u,\text{col}_v\) 的包含关系和子树大小即可,因为若子树大小关系正确,在之后的比较中我们会比较两棵子节点对应的子树是否同构,归纳可以发现其与原条件等价。
套用启发式合并,复杂度为 \(\mathcal{O}(n\log^2 n)\)。
loj3992. 「IOI2023」超车
考虑暴力的做法:对于每个 \(i\),维护出 \(s_{i,j}\) 表示巴士 \(j\) 到达调度站 \(i\) 的实际时间,显然有:
考虑怎么回答询问。注意到被备用巴士拖慢的巴士不影响答案,不妨将它们忽略。我们只需要对于每个调度站,求出备用巴士到达它的时间 \(Y_i\)。这个问题只需要每次二分找到 \(\max_{s_{i-1,k}<Y_i}s_{i-1,k}+w_k(s_i-s_{i-1})\) 即可仿照上面的过程轻松转移,不难使用前缀 max 维护。时间复杂度 \(\mathcal{O}(nm\log n+qm\log n)\)。code
考虑优化。发现这是一个经典套路:设 \(f_i(Y)\) 表示 \(Y\) 经过调度点 \(i\) 转移之后的时间,我们最后需要求的是 \(f_{0}(f_{1}(\cdots f_{m-2}(Y)))\)。可以发现 \(f_{i}(Y)\) 是一个不超过 \(2n\) 段的分段一次函数,所以可以考虑直接暴力维护出函数 \(g(Y)=f_{0}(f_{1}(\cdots f_{m-2}(Y)))\),其段数是不超过 \(2mn\) 的(经典结论:段数为 \(A\) 和一次函数 \(f\) 与段数为 \(B\) 的一次函数 \(g\) 复合得到的新函数 \(h\) 段数不超过 \(A+B\))。
合并两个分段函数有经典的 \(\mathcal{O}(A+B)\) 算法:每次找到 \(f\) 每一段在定义域上的区间 \([x_l,x_r]\),并求出其值域区间 \([y_l,y_r]\),然后取函数 \(g\) 在定义域为 \([y_l,y_r]\) 上的区间,还原到 \(f\) 上后扔进 \(h\) 里面,采用双指针即可。这个问题需要求 \(m\) 个函数的复合,所以需要套一个分治。每次求出 \(f_{[l,r]}(Y)\) 表示 \([l,r]\) 区间复合得到的分段函数,合并的时候令 \(f_{[l,r]}(Y)=f_{[l,mid]}(f_{[mid+1,r]}(Y))\) 即可,可以证明复杂度为 \(\mathcal{O}(nm\log m)\)。
回答询问的时候只需要二分找到 \(Y\) 所在的区间,总复杂度为 \(\mathcal{O}(nm\log m+q(\log n+\log m))\)。code