关系代数

概述

关系代数是研究数据库的一个重要工具，是一种抽象的查询语言，其运算的对象、结果均为关系。实际上关系的运算既包括关系运算，也包括集合运算，从细节入手还包括比较和逻辑运算。

原始运算

如同任何代数，一些运算是原始的，而可以通过原始运算来定义的另一些运算是导出的。

并（Union）

并操作($\cup$)的对象是两个集合R、S，返回一个新集合，这个新集合内元组的特点为：

\[R \cup S = \{ r | r \in R \vee r \in S \} \]

简单来讲，并操作消除了两个集合重复的元组（集合的性质），新关系（元组集合）中每个元组是唯一的。

进行并运算是有前提的，即R、S必须相容：

R与S必须同元，即属性数目必须相同
对任意i，R的第i个属性的域必须和S的第i个属性的域相同

也就是说，两个关系的格式必须一样，如果R有学号、姓名、年龄三种属性，那S有且仅有这三种属性，次序也要相同。

差（Minus）

差操作(-)的返回的新集合特点为：

\[R-S=\{ r | r \in R \wedge r \notin S \} \]

即R-S代表在R中但不在S中的元组的集合。

进行差运算是有前提的，即R和S必须同类型：

属性集相同（n目）
次序相同
属性名可以不同

交（Intersect）

交操作($\cap$)返回的新集合的特点为：

\[R \cap S = \{ r | r \in R \wedge r \in S \} \]

或者说：

\[R \cap S = R - (R - S) \]

即同时出现在两个关系中的元组的集合。

R和S必须满足同类型。

笛卡尔积

实质上是R与S的无条件连接，使得任意两个关系的信息可以组合在一起。

若R的关系为 $n_1 \times m_1$ ($n_1$行$m_1$目)，S的关系为 $n_2 \times m_2 $，则新关系$R \times S$ 为 $(n_1 \times n_2) \times (m_1 + m_2)$。

选择运算（σ）

选择运算($\sigma$)的操作对象为一个集合R，返回的结果为：

\[\sigma _{F(R)} = \{ t | t \in R, F(t) = true \} \]

$F$是选择的条件，对于 $\forall t \in R$，$F(t)$ 要么为真，要么为假，其形式包括：

逻辑表达式：$\vee , \wedge , \neg$
算术表达式：$X \theta Y$
$X 、Y$是属性名、常量或简单函数
$\theta$ 是比较算符，$\theta \in \{ > , < , \geq , \leq , = , \neq \}$

简单地理解就是从R中选出满足F为真的元组组成新元组。

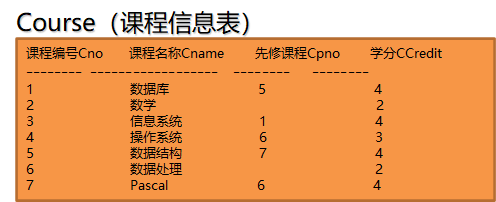
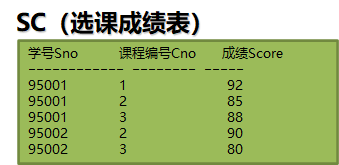
举个例子，如果我要筛选课程信息表中4学分的课程，那么我可以用下列表达式说明：

\[\sigma_{CCredit = 4(Course)} \]

或者将属性名用列序号代替：

\[\sigma_{4 = 4(Course)} \]

显然选择运算针对的是行，注意需要去除重复的分组。

投影运算（π）

投影运算($\Pi$ 音同 $\pi$)是从关系R中取若干列组成新的关系（集合）：

\[\Pi_A(R) = \{ t [A] | t \in R \} , A \subseteq R \]

$A$ 是一个属性（名），如下列的例子：

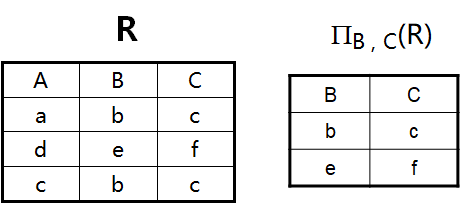
$\Pi_{A_1,A_2,...,A_n}(R)$表示从R中选择属性集$A_1,A_2,...,A_n$ 组成新的关系。

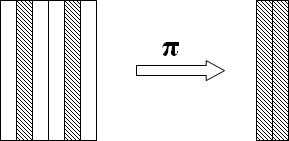
显然这是对列的运算，注意也需要去除重复的行。

改名运算（ρ）

改名运算可以改变关系名和属性名，将关系R改名为S，其表达式为：

\[S : \rho_S(R) \]

或者说我们想将关系$R(B_1,B_2,...,B_n)$改名为$S(A_1,A_2,...,A_n)$，其表达式为：

\[S(A_1,A_2,...,A_n):\rho_{S(A_1,A_2,...,A_n)}(R) \]

这样，我们可以得到具有不同名字的同一关系，对同一关系多次参与同一运算很有帮助。

连串（Concatenation）与笛卡尔积

连串是对元组而言的，若 $r = (r_1,...,r_n) ，s = (s_1,...,s_m) $，则定义r与s的连串为：

\[\mathop{rs}\limits^{\frown} = (r_1,...,r_n,s_1,...,s_m) \]

简单来说就是属性名的拼接，这种拼接是有顺序的（A和B不能交换）。

这时，我们的笛卡尔积表达式就可以表示为：

\[R \times S = \{ \mathop{rs}\limits^{\frown} | r \in R \wedge s \in S \} \]

我们也称之为广义笛卡尔积。

使用笛卡尔积进行关系内部选择比较

求数学成绩比王红高的学生：

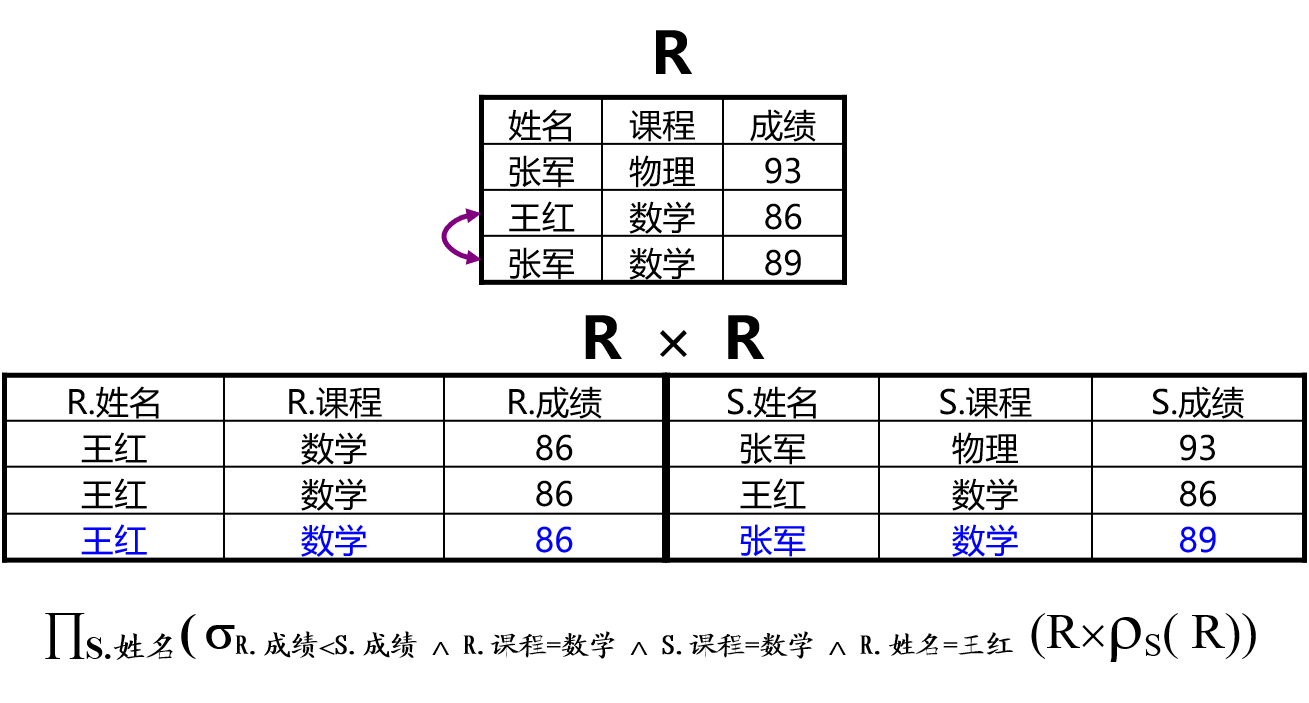
注意，这里有两个R，其中一个R改名为S，方便描述和运算。

连接（θ）及其类似的运算

（注意：在此不讨论半连接和反连接$\rtimes$,$\ltimes$,$\triangleright$)

从两个关系的广义笛卡尔积中选取给定属性间满足一定条件的元组：

\[\mathop{R \Join S}\limits_{A \theta B} = \{ \mathop{rs}\limits^{\frown} | r \in R \wedge s \in S \wedge r[A] \theta S[B] \} \]

注意：

A、B为R和S上度数相等且可比的属性列
$\theta$ 为算术比较符，为 = 时称为等值连接

用选择运算定义：

\[\mathop{R \Join S}\limits_{A \theta B} = \sigma_{r[A] \theta S[B]}(R \times S) \]

举个例子：

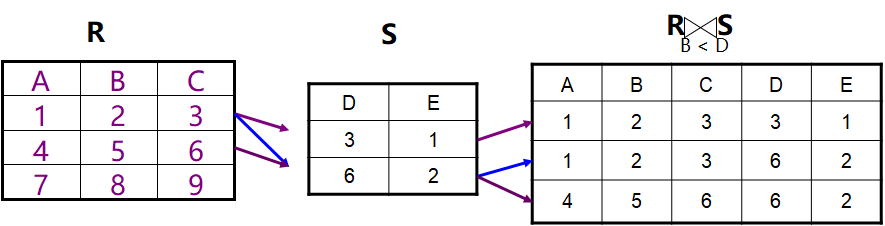
自然连接

从两个关系的广义笛卡儿积中选取在相同属性列B上取值相等的元组，并去掉重复的行，表达式为：

\[R \Join S = \{ \mathop{rs}\limits^{\frown}[B] | r\in R \wedge s \in S \wedge r[B] = S[B] \} \]

与等值连接的区别在于：属性组相同，去重。

举个例子：

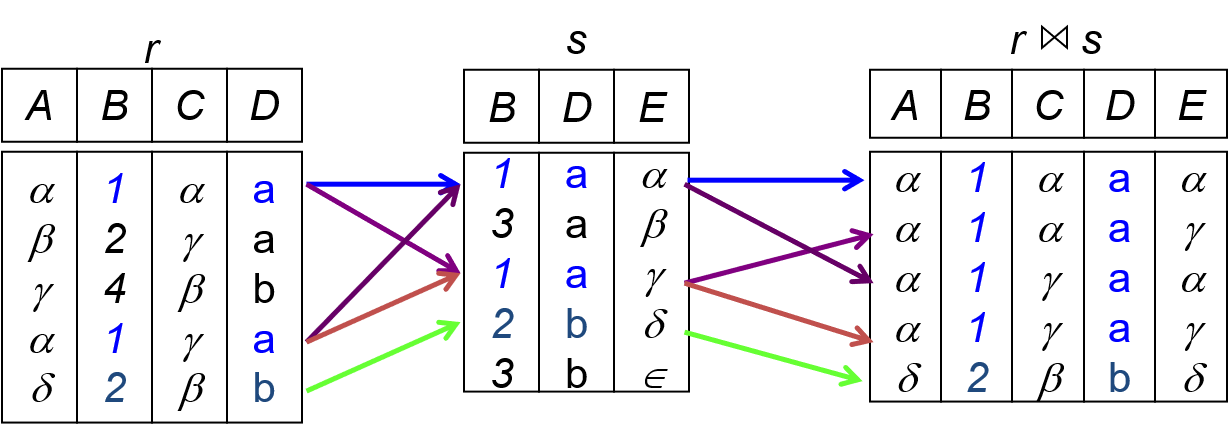
r与s的B、D两个属性重复，具体而言有3个子元组(BD)重复，为(1a,1a,2b)，2个1a内部做笛卡尔积，得到4个新元组，1个2b内部做笛卡尔积，得到1个新元组，组成自然连接的结果。

外连接

为避免自然连接时因失配而发生的信息丢失，可以假定往参与连接的一方表中附加一个取值全为空值的行，它和参与连接的另一方表中的任何一个未匹配上的元组都能匹配，称之为外连接。

外连接 = 自然连接 + 未匹配元组（悬挂元组）

外连接分为3种类型。

左外连接

⟕ = 自然连接 + 左侧表中未匹配元组

右外连接

⟖ = 自然连接 + 右侧表中未匹配元组

全外连接

⟗ = 自然连接 + 两侧表中未匹配元组

外连接的例子

左外连接：

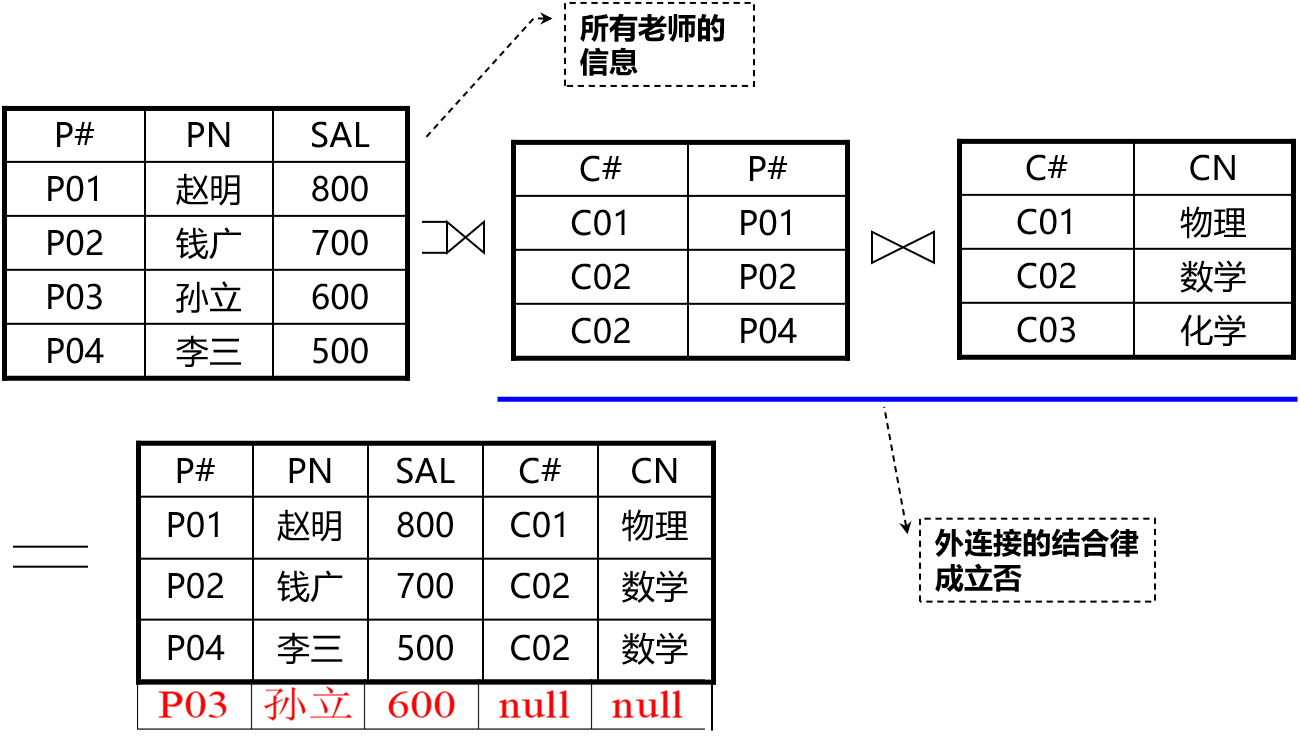
左侧老师信息和右侧已经过结合律完成连接的关系进行左外连接，此时发现P03的孙立，分数为600，没有匹配到，这时在自然连接的结果后补上一行元组，由于右侧没有对应的，所以C#和CN均为null。

右外连接：

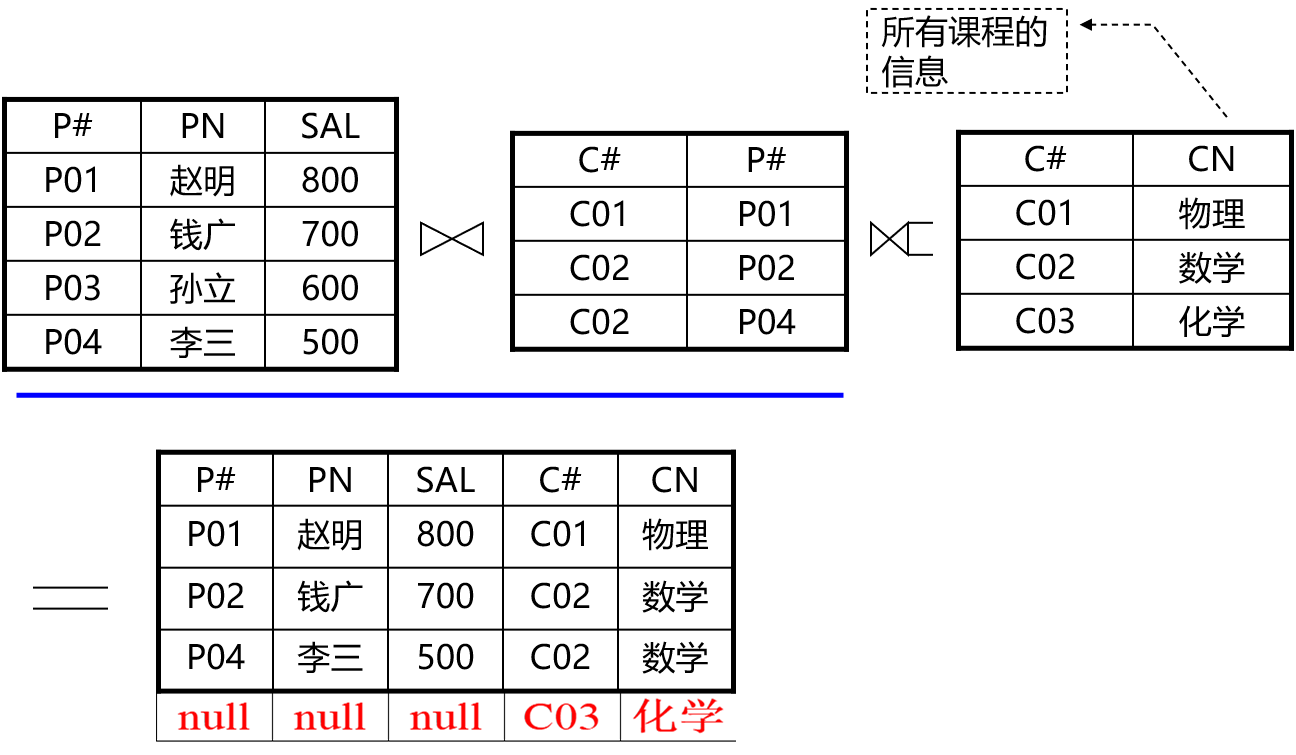
右侧所有课程的信息中C03化学没有匹配到，因此分配一个空的老师信息，给自然连接的结果添加一个新的（残缺）元组。

全外连接：

除法运算

除法运算($\div$)是写为$R \div S$的二元关系，其表达式为：

\[R \div S = \{ t[a_1,...,a_n] | t \in R \wedge \forall s \in S ((t[a_1,...,a_n] \cup s) \in R) \} \]

用投影来化简：

\[R \div S = \Pi_X(R) - \Pi_X( \Pi_X(R) \times \Pi_Y(S) - R) \]

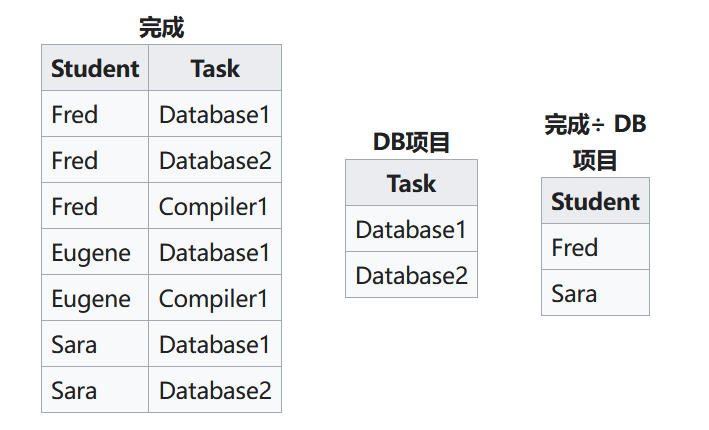
以上图为例，对于“完成”和“DB项目”两个关系，它们有Task这个共同属性，“完成”÷“DB”表示为完成了Database1和Database2

两个项目的学生构成的关系（表）。

赋值运算

其表达式为临时关系变量 ← 关系代数表达式

临时关系变量之所以叫临时关系变量是因为其不会对数据库作出实质的修改。

以上述除法的投影表达式为例，可以表示为：

\[temp_1 \gets \Pi_X(R) \]

\[temp_2 \gets \Pi_X(temp_1 \times \Pi_Y(S) - R) \]

\[result \gets temp_1 - temp_2 \]

事实上可以对已有的关系变量赋值，这时我们认为这是对数据库的修改。

广义投影

即用算术表达式对投影进行扩展。

比如求教工应缴纳的所得税，我们需要对工资进行换算才可以得到结果：

\[\Pi_{P\#,SAL*5/100}(PROF) \]

这里，选取了P#:教工名，和SAL:工资两个属性作为新关系，但是选取之后还要对SAL这一列上所有值*5/100，得到的就是所得税。

域计算的运算

聚集运算

多数数据库包括五个聚集函数。这些运算是Sum、Count、Average、Maximum和Minimum，可以简写为sum，count，avg，max，min等。

具体可以写为：

\[_{Exp1,Exp2,...}G_{func1,func2,...}(关系) \]

假定有一个叫Account的表有两列，分别是Branch_Name和Balance，并希望找到有最高结余的分部的名字，我们可以写$_{Branch\_Name}G_{Max(Balance)}(Account)$。要找到最高余额我们可以简单的写$G_{Max(Balance)}(Account)$。

接下来介绍几个运算，可以顺便介绍一种未分组的情况下简单的表示方法。