Note:[ wechat:Y466551 | 可加勿骚扰,付费咨询 ]
论文信息
论文标题:Meta-Tsallis-Entropy Minimization: A New Self-Training Approach for Domain Adaptation on Text Classification
论文作者:Menglong Lu、Zhen Huang、Zhiliang Tian、Yunxiang Zhao、Xuanyu Fei、Dongsheng Li
论文来源:2023 aRxiv
论文地址:download
论文代码:download
视屏讲解:click
1 介绍
动机:自训练从模型的预测中生成伪例子,并对伪例子进行迭代训练,即减少源域上的损失和目标域上的 Gibbs entropy。然而,Gibbs entropy 对预测误差很敏感,因此,当域位移较大时,自训练往往会失败;
贡献:
-
- 提出了用于文本分类的 MTEM,涉及一种近似技术来加速计算,以及一种退火采样机制来提高采样效率;
- 为 MTEM 提供了理论分析,包括它在实现领域自适应方面的有效性和所涉及的元学习过程的收敛性;
- 在两个基准数据集上的实验证明了 MTEM的 有效性:
- 在跨域情绪分类任务上的 BERT 平均高为4% ;
- 在跨域谣言检测任务上的 BiGCN 平均提高为 21% ;
2 相关
2.1 Tsallis entropy
Tsallis entropy 公式:
$e_{\alpha}\left(p_{i}\right)=\frac{1}{\alpha-1}\left(1-\sum_{j=1}^{K} p_{i[j]}^{\alpha}\right) \quad\quad(1)$
当 $\alpha>1$ 时,$e_{\alpha}$ 是一个凹函数。当 $\alpha \rightarrow 1$ 时,$e_{\alpha}$ 恢复为 Gibbs entropy:
$e_{\alpha \rightarrow 1}\left(p_{i}\right)=\frac{\lim _{\alpha \rightarrow 1} 1-\sum_{j=1}^{K} p_{i[j]}^{\alpha}}{\lim _{\alpha \rightarrow 1} \alpha-1}=\sum_{j=1}^{K}-p_{i[j]} \log \left(p_{i[j]}\right)\quad\quad(2)$
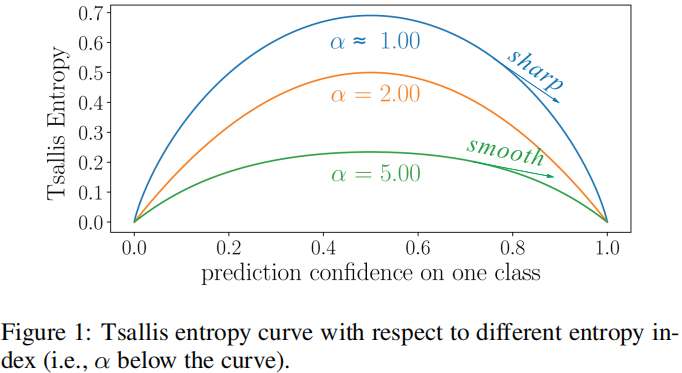
Note:Figure 1 显示了熵指数对 Tsallis entropy 曲线的影响:熵指数越大,曲线越平滑,熵指数越小,曲线越尖锐;
$\ell_{\alpha}\left(p_{i}, y_{i}\right)=\frac{1}{\alpha-1}\left(1-\sum_{j=1}^{K} y_{i[j]} \cdot p_{i[j]}^{\alpha-1}\right) \quad\quad(3)$
注意:当熵指数 $\alpha$ 很小时时,熵最小化过程倾向于将某一维急剧增加到 1.0,因此只适用于伪标签可靠的情况。否则,具有较大熵指数的 Tsallis entropy 更适合于具有较大标签噪声的场景,例如具有较大域位移的域适应场景。
动机:研究人员 [Liu et al.,2021] 试图使用 Tsallis entropy 来改善自训练,但只涉及到目标域内所有未标记数据的统一熵指数。如 [Kumar et al. 2010;Kumar et al. 2020] 所示,目标域中的不同实例从源域有不同程度的偏移。因此,一个统一的熵指数不能充分利用目标域中的不同伪实例。
2.2 域适应中的自训练
自训练目标函数:
$\underset{\theta}{\text{min}} \; \mathcal{L}_{S T}\left(\theta \mid D_{S}, D_{T}^{u}\right)=\mathcal{L}_{S}\left(\theta \mid D_{S}\right)+\lambda \cdot \mathcal{L}_{T}\left(\theta \mid D_{T}^{u}\right) \quad\quad(4)$
其中,$\mathcal{L}_{T}$ 为无监督损失,常采用吉布斯熵来测量目标域的预测不确定性:
$\mathcal{L}_{T}\left(\theta \mid D_{T}^{u}\right)=\frac{1}{\left|D_{T}^{u}\right|} \sum_{x_{i} \in D_{T}^{u}}-f\left(x_{i} ; \theta\right) \cdot \log \left(f\left(x_{i} ; \theta\right)\right) \quad\quad(5)$
注意:$\text{Eq.5}$ 中的 $\mathcal{L}_{T}\left(\theta \mid D_{T}^{u}\right)$ 是一个凹函数,最小化 $\mathcal{L}_{T}\left(\theta \mid D_{T}^{u}\right)$ 很难收敛,因为最小值上的梯度大于 $0$ 。因此,自训练使用伪标签来指导熵最小化过程,即用 $\text{Eq.6}$ 替换 $\text{Eq.5}$:
$\mathcal{L}_{T}\left(\theta \mid D_{T}^{u}\right)=\frac{1}{\left|D_{T}^{u}\right|} \sum_{x_{k} \in D_{T}^{u}}-\tilde{y}_{i}^{T} \cdot \log \left(f\left(x_{i} ; \theta\right)\right) \quad\quad(6)$
其中,$\tilde{y}_{i}= \underset{k}{\text{arg max}}\; f_{[k]}\left(x_{i} ; \theta\right)$ 是伪标签;
3 方法
模型框架
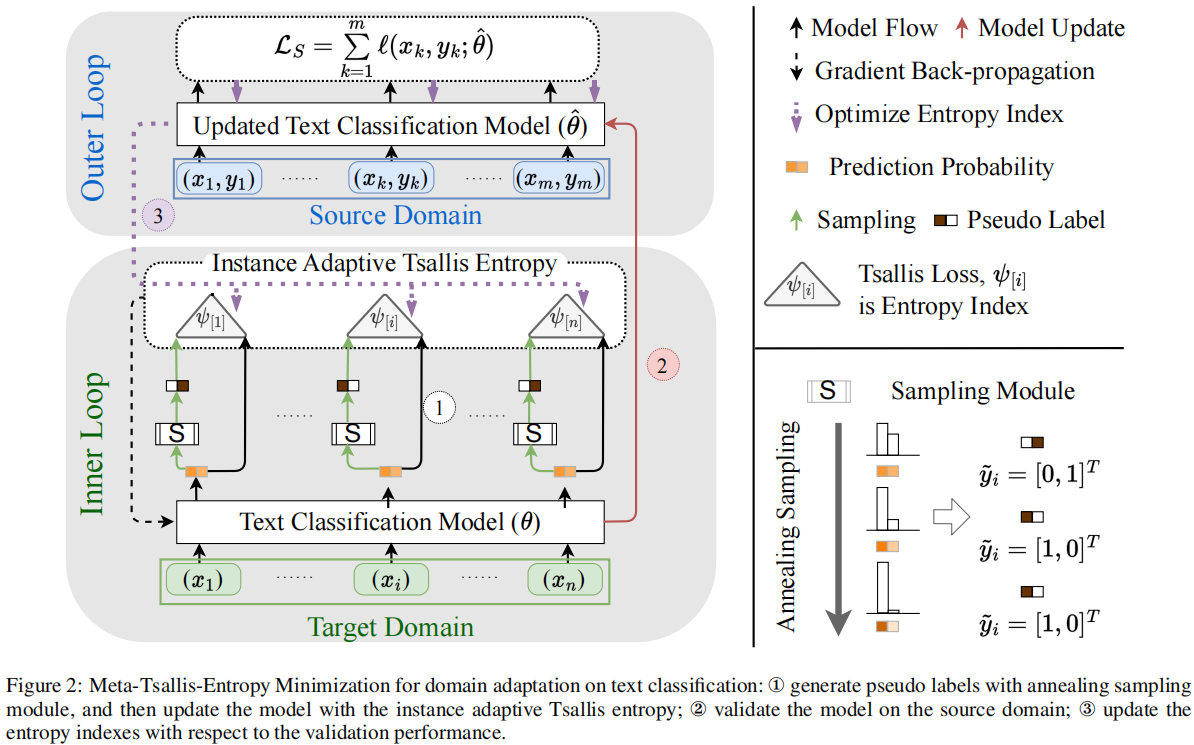
MTEM 继承了自训练的基本框架:
-
- 最小化源域上的监督损失和目标域上的无监督损失;
- 生成伪标签来指导熵最小化过程;
3.1 实例自适应 Tsallis Entropy
实例自适应 Tsallis Entropy,目标域上的无监督损失,如下:
$\mathcal{L}_{T}\left(\theta, \psi \mid D_{T}^{u}\right)=\frac{1}{\left|D_{T}^{u}\right|} \sum_{x_{k} \in D_{T}^{u}} e_{\psi_{[k]}}\left(f\left(x_{k} ; \theta\right)\right) \quad\quad(7)$
其中,$\psi_{[k]}$ 表示未标记数据 $x_{k}$ 的熵指数,$e_{\psi_{[k]}}$ 是 Tsallis Entropy;
由于不同实例的预测正确性是不同的,所以,熵指数在不同的实例上也应该是不同的。对于预测错误的情况,可以增加熵指数,使 Tsallis Entropy 更光滑,对模型的更新更加谨慎。对于预测正确的情况,可以设置一个小的熵指数来更积极地更新模型。然而,由于不知道类标签,所以为每个未标记的数据设置适当的熵索引是很棘手的。此外,由于在模型训练过程中预测误差可以得到修正,最佳熵指数会随着模型的更新而变化。为解决上述问题,建议使用元学习来自动确定熵指数。
3.2 元学习
算法:

MTEM 中的元学习算法在目标数据的内环和源域的外环上迭代。
内环:固定熵指数,通过优化 $\mathcal{L}_{T}(\theta, \psi \mid \mathcal{B})$ 更新模型参数:
$\hat{\theta}_{t+1}\left(\psi_{t}\right)=\theta_{t}-\left.\eta \cdot \frac{\partial \mathcal{L}_{T}\left(\theta, \psi_{t} \mid \mathcal{B}\right)}{\partial \theta}\right|_{\theta=\theta_{t}} \quad\quad(8)$
由于 $e_{\psi}$ 是一个难优化的凹函数,所以使用 $\text{Eq.9}$ 将 $\text{Eq.8}$ 转换为 一个凸函数:
$e_{\psi}\left(f\left(x_{i} ; \theta_{t}\right)\right)= \underset{\tilde{y}_{i} \sim f\left(x_{i} ; \theta_{t}\right)}{\mathbb{E}} \;\; \ell_{\psi_{[i]}}\left(f\left(x_{i} ; \theta_{t}\right), \tilde{y}_{i}\right) \quad\quad(9)$
内环目标:
$\underset{\theta}{\text{min}} \; \mathcal{L}_{T}\left(\theta, \psi \mid D_{T}^{u}\right)=\underset{\tilde{y}_{i} \sim f\left(x_{i} ; \theta\right)}{\mathbb{E}} \frac{1}{\left|D_{T}^{u}\right|} \sum_{x_{i} \in D_{T}^{u}} \ell_{\psi_{[i]}}\left(f\left(x_{i} ; \theta\right), \tilde{y}_{i}\right) \quad\quad(10)$
外环:使用来自源域的标记数据验证模型,最小化损失 $\mathcal{L}_{S}\left(\hat{\theta}_{t+1}\left(\psi^{t}\right) \mid \mathcal{V}\right) $ ,然后使用 $\nabla_{\psi} \mathcal{L}_{S}\left(\hat{\theta}_{t+1}\left(\psi^{t}\right) \mid \mathcal{V}\right)$ 更新熵指数 $\psi_{t+1}$。
3.3 Taylor Approximation Technique
问题:上述计算 $\nabla{ }_{\psi} \mathcal{L}_{S}\left(\hat{\theta}_{t+1}\left(\psi^{t}\right) \mid \mathcal{V}\right)$ 成本太高。在形式上,$\nabla_{\psi} \mathcal{L}_{S}\left(\hat{\theta}_{t+1}\left(\psi^{t}\right) \mid \mathcal{V}\right)$ 的计算方法为:
$\begin{aligned}\frac{\partial \mathcal{L}_{S}\left(\hat{\theta}_{t+1}\left(\psi^{t}\right) \mid \mathcal{V}\right)}{\partial \psi}= & \frac{\partial \mathcal{L}_{S}\left(\hat{\theta}_{t+1}\left(\psi_{t}\right) \mid \mathcal{V}\right)}{\partial \hat{\theta}_{t+1}\left(\psi_{t}\right)} \cdot \frac{\partial \hat{\theta}_{t+1}\left(\psi_{t}\right)}{\partial \psi} \\= & -\eta \nabla_{\hat{\theta}} \mathcal{L}_{S}\left(\hat{\theta}_{t+1}\left(\psi_{t}\right) \mid \mathcal{V}\right) \frac{\partial^{2} \mathcal{L}_{T}\left(\theta, \psi_{t} \mid \mathcal{B}\right)}{\partial \theta \partial \psi}\end{aligned} \quad\quad(11)$
Note:
-
- $\hat{\theta}_{t+1}\left(\psi^{t}\right)$ 是用 $\text{Eq.8}$ 代替得到的;
- $\hat{\theta}_{t+1}\left(\psi^{t}\right)$ 是一个海色矩阵,二阶推导,计算成本是二次的;
本文提出一种计算近似技术来重写 Eq.11 中的 $\frac{\partial \mathcal{L}_{S}(\hat{\theta}(\psi))}{\partial \hat{\theta}} \frac{\partial^{2} \mathcal{L}_{T}(\psi)}{\partial \theta \partial \psi}$,使用泰勒展开式近似为:
$\nabla_{\hat{\theta}} \mathcal{L}_{S}\left(\hat{\theta}_{t+1}\left(\psi_{t}\right) \mid \mathcal{V}\right) \cdot \frac{\partial^{2} \mathcal{L}_{T}(\theta)}{\partial \theta \partial \psi} =\frac{\nabla_{\psi} \mathcal{L}_{T}\left(\theta^{+}\right)-\nabla \psi \mathcal{L}_{T}\left(\theta^{-}\right)}{2 * \epsilon} \quad\quad(12)$
其中,$\epsilon$ 为一个小标量,$\theta^{+}$ 和 $\theta^{-}$ 定义如下:
$\begin{array}{l}\theta^{+}=\theta+\epsilon \cdot \nabla_{\hat{\theta}} \mathcal{L}_{S}\left(\hat{\theta}_{t+1}\left(\psi_{t}\right) \mid \mathcal{V}\right)\\\theta^{-}=\theta-\epsilon \cdot \nabla_{\hat{\theta}} \mathcal{L}_{S}\left(\hat{\theta}_{t+1}\left(\psi_{t}\right) \mid \mathcal{V}\right)\end{array} \quad\quad(13)$
如 [Liu et al,2018] 所示,$\text{Eq.12}$ 在 $\epsilon $ 很小时,将具有足够精确的近似值。然而,在 $\text{Eq.12}$ 中计算 $\nabla \psi \mathcal{L}_{T}$ 仍然需要大量的计算成本,因为它涉及到一个前向操作 $\mathcal{L}_{T}$ 和一个后向操作 $\nabla \psi \mathcal{L}_{T}$ 。为此,推导出 $\nabla \psi \mathcal{L}_{T}$ 的显式形式为 $\text{Eq.14}$:
$\nabla \psi_{[i]} \mathcal{L}_{T}(\theta)=\frac{1}{\psi_{[i]}-1} \times\left[l_{1}\left(x_{i}, \tilde{y}_{i}\right)-l_{\psi_{[i]}}\left(x_{i}, \tilde{y}_{i}\right)\right]-l_{1}\left(x_{i}, \tilde{y}_{i}\right) \times l_{\psi_{[i]}}\left(x_{i}, \tilde{y}_{i}\right) \quad\quad(14)$
$\text{Eq.14}$ 中的 $l_{1}\left(x_{i}, \tilde{y}_{i}\right)$ 和 $l_{\psi_{[i]}}$ 可不进行梯度计算,防止了耗时的反向传播过程。
3.4 Annealing Sampling
在域自适应中,内环中的朴素采样机制会出现低效率采样问题。当域移较大时,模型在目标域的表现通常比在源域差。因此,模型对真实类的预测置信度很小。考虑极端二值分类情况,实例的地面真实标签为 $[0,1]_{t}$,而模型的预测为 $[0.99,0.01]_{t}$,对地面真实标签进行的采样概率为 0.01。在这种情况下,大部分的训练成本被浪费在带有错误标签的伪实例上。
为了提高采样效率,提出了一种退火采样机制。利用温度参数 $\kappa$,通过 $p\left(\bullet ; \theta, x_{i}, \kappa\right)=\operatorname{softmax}\left(\frac{\text { score }}{\kappa}\right)$ 来控制模型的预测概率的锐度,其中 $p$ 为采样概率,$score$ 为模型的原始预测分数。在早期的训练阶段,模型的预测不太可靠,所以设置了一个高温参数 $\kappa$ 来平滑模型的预测分布。在此设置下,对不同的类别标签以大致相等的概率进行采样,这保证了对正确的伪标签进行采样的可能性。随着训练过程的收敛性,模型的预测越来越可靠,因此温度调度器会降低模型的温度。本文设计了一个温度调度器:
$\kappa_{t}=\kappa_{\max }-\left(\kappa_{\max }-\kappa_{\min }\right) \sigma\left(s-2 s \times \frac{t}{T_{\max }}\right)$
其中 $\sigma$ 为 $\text{sigmoid}$ 函数,$\kappa_{\max } $ 和 $\kappa_{\min }$ 为期望的最高温度和最低温度,$s$ 为手动设置的标量。$t$ 为当前训练迭代轮次,$T_{\max }$ 为训练迭代的最大值。因此,$ \frac{t}{T_{\max }}$ 从 0.0 增加到 1.0,输入的 $s-2 s \times \frac{t}{T_{\max }}$ 从 $s$ 减少到 $−s$。在本文的实现中,$s$ 的值很大,满足 $\sigma(s) \approx 1.0$ 和 $\sigma(-s) \approx 0.0$,这保证了 $\kappa_{t}$ 将从 $\kappa_{\max }$ 减少到 $\kappa_{\min }$。
4 实验
数据集
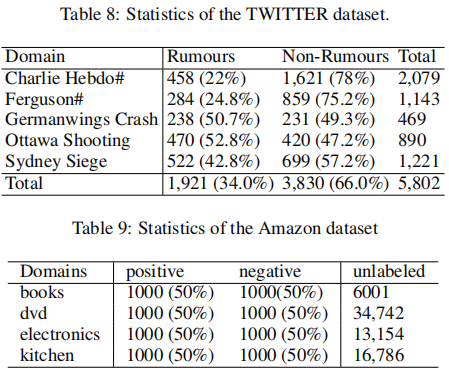
- Meta-Tsallis-Entropy Classification Self-Training Minimization Adaptationmeta-tsallis-entropy classification self-training self-training adaptation training domain meta-tsallis-entropy self-training minimization minimization atcoder regular contest transduction minimization alternating graph minimization empirical beyond mixup sharpness-aware generalization minimization reinforcement minimization experience off-policy