Preface
咕咕咕咕咕咕咕了半年有余。不得不说这题真的会把你调炸!!!!!!11
本题解中的所有 Hints 以白字显示。所以它可能不适合手机观看。
以及,首黑,2022 年 7 月 31 日 15:51。
Solution
算法一
询问次数 $2^h - 2$,适用于 $h \leq 4$。
- Hint 0:$\color{white}\texttt{请注意,你必须设计一个确定性的算法,即使随机化算法只有非常小的几率使用超过 16 次询问。}$
- Hint 1:$\color{white}\texttt{根节点的度数为 2。}$
- Hint 2:$\color{white}\texttt{在所有根节点备选方案中,如已确定其余所有都不是根节点,会如何?}$
- Hint 3:$\color{white}\texttt{根节点即为最后一个没有被排除的。这提示我们 16 次操作实际上是 17 次操作。}$
对 $1$ 到 $2^h - 1$ 依次询问,判断其邻居个数是否为 $2$。
算法二
询问次数 $\dfrac{1}{2}(h^2-h)$ 或 $\dfrac{1}{2}(h^2-5h+18)$ 或 $\dfrac{1}{2}(h^2-5h+16)$,适用于 $h \leq 6$ 或 $h \leq 7$。
下文的「上」指的是向深度低的节点搜索,反之「下」指的是向深度高的节点搜索。
- Hint 4:$\color{white}\texttt{一条从 x 出发最后到达叶子节点的路径,一定是先向上走到与 x 的任意一个祖先(包括 x),再掉头一直向下走。}$
- Hint 5:$\color{white}\texttt{两个节点的深度相同,它们的 lca 在它们的路径中点上。}$
取一个初始点 $x$,在其度数为 $3$ 时,向外扩展以降低深度。考虑每次扩展,我们肯定是要找一条路径。首次扩展时选择两条路径直到找到叶子。对于已知的两条到达叶子的路径,显然它们路径的中点是它们的 $\text{lca}$。
- 如果我们找到的两条路径的 $\text{lca}$ 是 $x$,那么相当于我们确定了 $x$ 的三条连边中向下的两条路径。所以我们可以得出 $x$ 的父亲。如果 $x$ 的度数为 $1$,则可以跳过这一步。
- 否则,可以证明这个新的 $\text{lca}$ 是 $x$ 的祖先。而对于这个节点,同样有我们知道了其三条连边中向下的两条路径。
对于新的节点,直接从其上方搜索一条路径即可。
综上所述,我们可以一直迭代直到找到度数为 $2$ 的节点。
这样做的最劣复杂度是什么?可以看一张 $h = 7$ 的图:
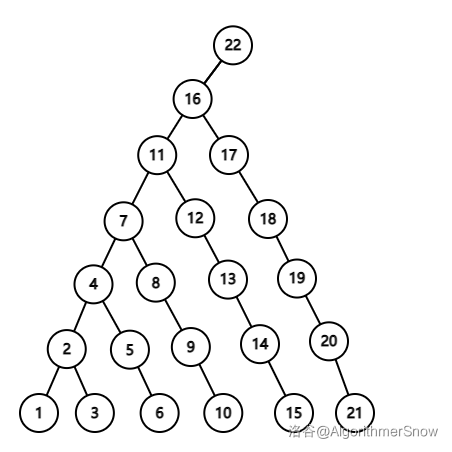
容易证明这是最劣情况,共需询问 $\dfrac{1}{2}(h^2-h) = 21$ 次。(为什么不是 $22$ 次?考虑上文的 Hints 2 & 3)
考虑优化。
- Hint 6:最小的最劣会超出 $16$ 次询问次数的深度为?$\color{white}\texttt{4,询问次数分别为:1,11,15,18,20,21,21}$
根据这个 Hint,我们考虑起始深度 $\leq 3$ 是可以直接通过的。
如果起始深度 $\geq 4$,那么最劣情况下,$12$ 次询问我们已经可以确定一个深度 $= 3$ 的节点位置和其两个向下的方向。(如果依旧不能确定这样一个节点,$16$ 次询问——或者更少,可以特判——我们可以保证确定一个深度 $= 2$ 的节点位置和其两个向下的方向,可以通过)在确定一个深度如此接近根节点的节点后,考虑直接找其相邻的距离为 $2$ 的两个不确定的邻居。询问次数最劣是 $\dfrac{1}{2}(h^2-5h+18)$ 或 $\dfrac{1}{2}(h^2-5h+16)$ 基于不同实现,可以通过 $h \leq 7$ 的数据。
- 剪枝:如果 $h = 7$ 且知道了 lca 深度为 $4$,直接给它跳到深度为 $3$ 的节点(其它深度都不需要特判,手玩一下即可)。
Code
#include <bits/stdc++.h>
constexpr int MaxNode = 127;
std::vector<int> neighbours[MaxNode + 1];
int depth[MaxNode + 1];
int query(int u) {
if (!neighbours[u].empty()) return neighbours[u].size();
std::cout << "? " << u << std::endl;
static int ans, p; std::cin >> ans;
if (ans == 0) exit(0);
while (ans--) {
std::cin >> p;
neighbours[u].push_back(p);
}
return neighbours[u].size();
}
void judge(int u) {
std::cout << "! " << u << std::endl;
for (int i = 1; i <= MaxNode; ++i)
neighbours[i].clear();
memset(depth, 0, sizeof(depth));
}
std::vector<int> lcapath(std::vector<int> A, std::vector<int> B, int H) {
std::reverse(A.begin(), A.end());
int N = (A.size() + B.size()) / 2;
std::vector<int> ans;
for (int i = 1; i < B.size(); ++i) A.push_back(B[i]);
for (int i = 0; i < A.size(); ++i)
depth[A[i]] = H - std::min(i, (int)A.size() - i - 1);
for (int i = 0; i < N; ++i) ans.push_back(A[i]);
std::reverse(ans.begin(), ans.end());
return ans;
}
constexpr int Start_Point = 1;
void interactive() {
int H, current = Start_Point;
std::cin >> H;
if (H == 0) exit(0);
std::vector<int> pathA, pathB;
pathA.push_back(current), pathB.push_back(current);
while (query(pathA.back()) != 1) {
if (query(pathA.back()) == 2)
return (void)judge(pathA.back());
for (auto u : neighbours[pathA.back()])
if (neighbours[u].empty()) {
pathA.push_back(u);
break;
}
}
while (query(pathB.back()) != 1) {
if (query(pathB.back()) == 2)
return (void)judge(pathB.back());
for (auto u : neighbours[pathB.back()])
if (neighbours[u].empty()) {
pathB.push_back(u);
break;
}
}
if (pathA.size() == 1 && pathB.size() == 1) {
pathA.push_back(neighbours[current][0]);
pathB.push_back(neighbours[current][0]);
std::reverse(pathA.begin(), pathA.end());
std::reverse(pathB.begin(), pathB.end());
}
pathA = lcapath(pathA, pathB, H);
pathB = std::vector<int>(1, pathA.front());
while (true) {
if (depth[pathA.front()] == 4 && H == 7) {
std::reverse(pathA.begin(), pathA.end());
for (auto u : neighbours[pathA.back()])
if (neighbours[u].empty())
pathA.push_back(u), depth[u] = 3;
std::reverse(pathA.begin(), pathA.end());
}
if (depth[pathA.front()] == 3 && H == 7) {
query(pathA.front());
std::vector<int> sel;
for (auto u : neighbours[pathA.front()]) {
query(u); for (auto v : neighbours[u])
if (neighbours[v].empty()) sel.push_back(v);
}
for (auto i : sel) if (i == sel.back())
return (void)judge(i);
else if (query(i) == 2) return (void)judge(i);
exit(-1);
}
if (depth[pathA.front()] == 2 && H == 7) {
query(pathA.front());
std::vector<int> sel;
for (auto u : neighbours[pathA.front()])
if (neighbours[u].empty()) sel.push_back(u);
for (auto i : sel) if (i == sel.back())
return (void)judge(i);
else if (query(i) == 2) return (void)judge(i);
exit(-2);
}
while (query(pathB.back()) != 1) {
if (query(pathB.back()) == 2)
return (void)judge(pathB.back());
for (auto u : neighbours[pathB.back()])
if (neighbours[u].empty()) {
pathB.push_back(u);
break;
}
}
pathA = lcapath(pathA, pathB, H);
pathB = std::vector<int>(1, pathA.front());
}
}
int main() {
int T; std::cin >> T;
while (T--) interactive();
return 0;
}
Postscript
算法三
基于其他题解的思路:以一个点作为起始点,bfs 搜索。
- 这样做的好处是,在深度小的时候可以明显减小搜索次数。
- 但是,当深度越来越大时,需要代码实现趋近于 dfs。
- 这也是原有的题解做法存在的问题:如果我把 $h$ 开大一点,你不得不考虑写一大堆剪枝来达到模拟 dfs 的效果。
代码实现本来是有的,但是我调炸了,一开始写的就是这种做法结果调到吐血最后不得已自己独立推出了官方题解做法(也就是这里的算法二),所以看其他题解去吧。
算法四
来自于 cnyz,他后来隐藏了博客。
大概就是对于每个 $(h, dep)$ 预处理 bfs 一圈和向上哪种是更优的,然后就能通过了,不用分类讨论。