数据收集与清洗
最近的项目有一个需求是需要根据手机传感器的信息,对用户进行动作识别。
动作识别是通过一系列用户动作的记录和环境状况的数据,判断用户的运动状态(motion activity)。项目的需求仅限于根据数据判断用户的运动状态,如步行,跑步,驾车,骑车等。
采集数据采用的手机中的加速度计(accelerometer),Android的核心代码就是记录加速度计的数据以及当前行为状态的真值。采集的频率为 50Hz,综合考虑了耗电和存储的限制。同时在采集数据时,记录了Samsung motion API和Google Activity Recognition的数据,用来和项目最终的效果做一个对比。
public void onSensorChanged(SensorEvent sensorEvent) {
if(sensorEvent.sensor.getType()== Sensor.TYPE_ACCELEROMETER){
float x = sensorEvent.values[0];
float y = sensorEvent.values[1];
float z = sensorEvent.values[2];
mLogger.info("record: " + mStatus + " [" + x + "," + y + "," + z + "]");
}
}
根据奈奎斯特采样定理,在进行模拟/数字信号的转换过程中,当采样频率fs.max大于信号中最高频率fmax的2倍时(fs.max > fmax * 2),采样之后的数字信号完整地保留了原始信号中的信息,一般实际应用中保证采样频率为信号最高频率的2.56~4倍。虽然我们按照50Hz的标准来采集数据,但是在我们分析数据时,为了保证数据的完整性,应该只取用25Hz。
同时,动作识别需要根据一系列的数据来进行分析,单点的数据不能得到任何信息,因此,需要考虑的就是应该截取多大的时间段来做动作识别的分析。傅里叶变换要求要完整地分析一段离散的数据,那么这段数据中最大的周期应该包含在里面。多种动作中以步行的周期最大,此处暂定2s的时间段来进行分析。如果2s的时间段中覆盖了完整的行为周期,那么绘制出的傅里叶变换图像也应该是对称的。
傅里叶变换,特征抽取
本文的目的并不是要讲述动作识别的实现过程,而是要说明在特征抽取的过程中,最为重要的特征的理论说明和实现。
手机中采集的加速度计的数据是时域的信号,但是当我们需要对信号进行分析时,需要将时域的信号转换到频域中,并从中抽取出特征进行分析。
由于我们所采集的数据是离散的周期性数据,所以就对应离散傅里叶变换。随机抽取两条驾车和两条步行的数据,绘制图像:
import sys
import numpy as np
import matplotlib.pyplot as plt
PERIOD = 2 #s,时间间隔
FREQ = 50 #Hz,样本频率
cs = ['red', 'blue']
lab = ['car', 'walk']
count = 0
plt.figure(figsize = (10,8))
p1 = plt.subplot(211)
p2 = plt.subplot(212)
for line in sys.stdin:
info = line.strip().split('\t')
state = info[0]
x = map(float, info[1].split(','))
if state == 'bus':
p1.scatter(np.linspace(0, FREQ, len(x)), np.absolute(np.fft.fft(x)), c= cs[count%2], \
label = state + str(count%2), s = 30, alpha = (count + 1) * 0.2)
elif state == 'walk':
p2.scatter(np.linspace(0, FREQ, len(x)), np.absolute(np.fft.fft(x)), c= cs[count%2], \
label = state + str(count%2), s = 30, alpha = (count + 1) * 0.2)
else:
continue
count = count + 1
p1.legend()
p1.axis([-10.0,60.0, -10.0,50.0])
p1.set_xlabel('Freq(Hz)')
p1.set_ylabel('fft')
p2.legend()
p2.axis([-10.0,60.0, -10.0,50.0])
p2.set_xlabel('Freq(Hz)')
p2.set_ylabel('fft')
#plt.show()
plt.savefig('./all.png')
得到这四条记录的图像:
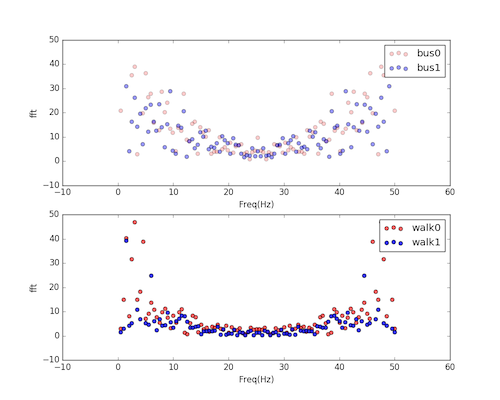
从图像就可以看出,同是步行的数据基本都重叠在一起,同是驾车的数据也基本都重叠在一起,也就是说我们通过分析傅里叶变换之后不同频率的数据的值来作为特征判断用户的动作。
为了直观感受驾车和步行在频域的区别,分别抽取一条步行和一条驾车的数据,绘制图像:
import sys
import numpy as np
import matplotlib.pyplot as plt
PERIOD = 2
FREQ = 50
cs = ['red', 'blue']
lab = ['car', 'walk']
count = 0
plt.figure(figsize = (10,5))
for line in sys.stdin:
info = line.strip().split('\t')
state = info[0]
x = map(float, info[1].split(','))
plt.scatter(np.linspace(0, FREQ, len(x)), np.absolute(np.fft.fft(x)), c = cs[count], label = state, s = 30, alpha = (count + 1) * 0.3)
count = count + 1
plt.legend()
plt.xlim(-10, 60)
plt.ylim(-10, 50)
plt.xlabel('Freq(Hz)')
plt.ylabel('fft')
#plt.show()
plt.savefig('./car_walk.png')
得到两条记录的图像:
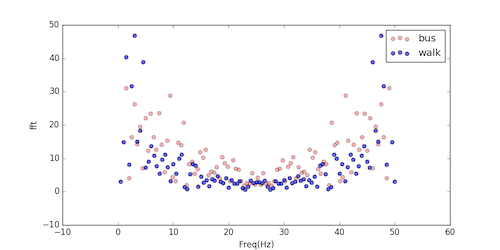
从步行和驾车的图像对比来看,在低频阶段我们可以看到步行的值比驾车要高,但是在高频阶段,驾车的值要比步行的值要高,所以在采取特征进行训练时,我们考虑以下特征:
x_spec = np.fft.fft(xlist)
y_spec = np.fft.fft(ylist)
z_spec = np.fft.fft(zlist)
m_spec = np.fft.fft(magni)
x_f1 = np.sum(np.absolute(x_spec[:Period]))
y_f1 = np.sum(np.absolute(y_spec[:Period]))
z_f1 = np.sum(np.absolute(z_spec[:Period]))
m_f1 = np.sum(np.absolute(m_spec[:Period]))
x_f2_3 = np.sum(np.absolute(x_spec[2*Period:3*Period]))
y_f2_3 = np.sum(np.absolute(y_spec[2*Period:3*Period]))
z_f2_3 = np.sum(np.absolute(z_spec[2*Period:3*Period]))
m_f2_3 = np.sum(np.absolute(m_spec[2*Period:3*Period]))
x_f1_3 = np.sum(np.absolute(x_spec[1*Period:3*Period]))
y_f1_3 = np.sum(np.absolute(y_spec[1*Period:3*Period]))
z_f1_3 = np.sum(np.absolute(z_spec[1*Period:3*Period]))
m_f1_3 = np.sum(np.absolute(m_spec[1*Period:3*Period]))
x_f4_5 = np.sum(np.absolute(x_spec[4*Period:5*Period]))
y_f4_5 = np.sum(np.absolute(y_spec[4*Period:5*Period]))
z_f4_5 = np.sum(np.absolute(z_spec[4*Period:5*Period]))
m_f4_5 = np.sum(np.absolute(m_spec[4*Period:5*Period]))
x_f6_16 = np.sum(np.absolute(x_spec[6*Period:16*Period]))
y_f6_16 = np.sum(np.absolute(y_spec[6*Period:16*Period]))
z_f6_16 = np.sum(np.absolute(z_spec[6*Period:16*Period]))
m_f6_16 = np.sum(np.absolute(m_spec[6*Period:16*Period]))
x_f4_16 = np.sum(np.absolute(x_spec[4*Period:16*Period]))
y_f4_16 = np.sum(np.absolute(y_spec[4*Period:16*Period]))
z_f4_16 = np.sum(np.absolute(z_spec[4*Period:16*Period]))
m_f4_16 = np.sum(np.absolute(z_spec[4*Period:16*Period]))
傅里叶分析
之前没有学习过傅里叶分析,因为这次项目需要,所以就或多或少地了解了一些用来应对项目。
你眼中看似落叶纷飞变化无常的世界,实际只是躺在上帝怀中一份早已谱好的乐章。 看上去这么诗意的一句话其实是教材上对傅里叶分析的介绍。
傅里叶分析分为傅里叶级数(Fourier Serie)和傅里叶变换(Fourier Transformation)。法国数学家傅里叶发现,任何周期函数都可以用正弦函数和余弦函数构成的无穷级数来表示(选择正弦函数和余弦函数作为基函数是因为他们是正交的),暂时不考虑证明!
傅里叶级数
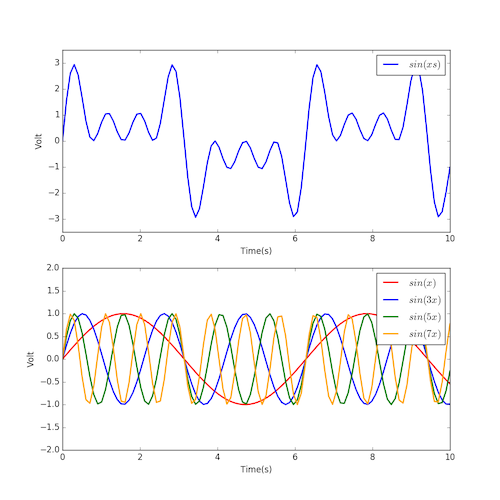
上图是sin(x) + sin(3x) + sin(5x) + sin(7*x)的图像以及它们分开的各自的图像。当这几个函数分开时,我们还是可以进行分辨的,但是一旦将它们组合在一起,我们无法分辨这个函数,也使得我们无法对其进行处理和提取信息。
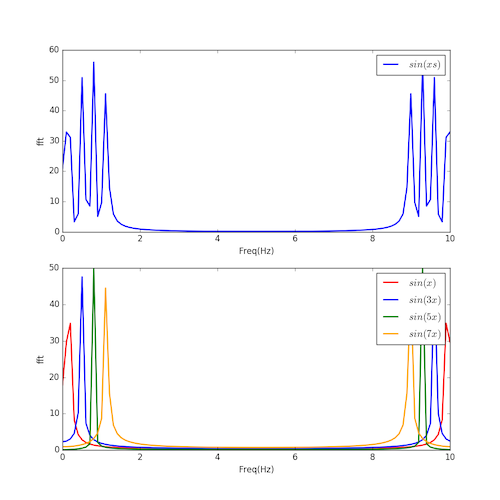
对应上一幅图中在时域的图像,这幅图显示了之前的函数在频域的图像,我们可以看出之前复杂的函数被分拆成多个函数的组合,以上是傅里叶级数的应用,实际可以用来进行信号的过滤,声音的提取等。
傅里叶分析究竟是干什么用的?这段相对比较枯燥,已经知道了的同学可以直接跳到下一个分割线。
先说一个最直接的用途。无论听广播还是看电视,我们一定对一个词不陌生——频道。频道频道,就是频率的通道,不同的频道就是将不同的频率作为一个通道来进行信息传输。下面大家尝试一件事:
先在纸上画一个sin(x),不一定标准,意思差不多就行。不是很难吧。
好,接下去画一个sin(3x)+sin(5x)的图形。别说标准不标准了,曲线什么时候上升什么时候下降你都不一定画的对吧?
好,画不出来不要紧,我把sin(3x)+sin(5x)的曲线给你,但是前提是你不知道这个曲线的方程式,现在需要你把sin(5x)给我从图里拿出去,看看剩下的是什么。这基本是不可能做到的。
但是在频域呢?则简单的很,无非就是几条竖线而已。
所以很多在时域看似不可能做到的数学操作,在频域相反很容易。这就是需要傅里叶变换的地方。尤其是从某条曲线中去除一些特定的频率成分,这在工程上称为滤波,是信号处理最重要的概念之一,只有在频域才能轻松的做到。
再说一个更重要,但是稍微复杂一点的用途——求解微分方程。(这段有点难度,看不懂的可以直接跳过这段)微分方程的重要性不用我过多介绍了。各行各业都用的到。但是求解微分方程却是一件相当麻烦的事情。因为除了要计算加减乘除,还要计算微分积分。而傅里叶变换则可以让微分和积分在频域中变为乘法和除法,大学数学瞬间变小学算术有没有。
傅里叶变换
傅里叶级数的本质是将一个周期的信号分解成无限多分开的(离散的)正弦波。
但是,我们在实际的应用中,遇到更多的是非周期的数据,而且我们也意识到无法将连续的非周期信号变换为周期的离散信号。
在傅里叶变换中,如果在时域的信号是周期离散的数据,那么对应在频域的信号就是非周期的离散的数据。
如果在时域的信号是周期连续的数据,那么对应在频域的信号就是非周期的连续的数据,对于单一的正余弦函数,是一条单一的直线。
参考资料: